2.(1)已知函数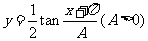的最小正周期为3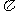，则A= 　　　___ .　

(2)函数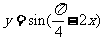的单调增区间是_______________________.

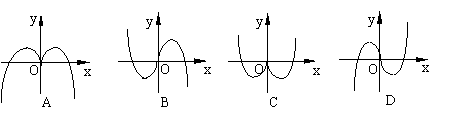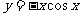1. 函数的部分图象是 (　 　　) .

3. 已知三角函数求角时应注意：角的取值范围，以及非特殊角的正确表示.

2.(1)五点作图法的步骤：求周期；取起点、终点；四等分；描点作图.

(2)看图说话问题一般按：A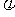，，的顺序求解，注意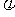的求解方法和取值范围 .

(3)三角函数的对称问题：对称轴 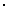　最值；对称中心 　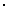零点 .

1.求：周期，单调区间，最值的三角问题，先将解析式化为.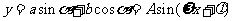

2. 会用“五点法”画正弦函数、余弦函数和函数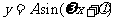的简图，理解的意义.

1. 理解正弦函数、余弦函数、正切函数的图像和性质

7.[答案](1)EF=EB．证明：如图，以E为圆心，以EA为半径画弧交直线m于点M,连结EM．

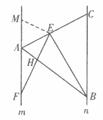
∴EM=EA, ∴∠EMA=∠EAM．

∵BC=Kab,k=1，∴BC=AB．

∴∠CAB=∠ACB．

∵m∥n，∴∠MAC=∠ACB, ∠FAB=∠ABC．

∴∠MAC=∠CAB．

∴∠CAB=∠EMA．

∵∠BEF=∠ABC, ∴∠BEF=∠FAB．

∵∠AHF=∠EHB, ∴∠AFE=∠ABE．

∴△AEB≌△MEF．

∴EF=EB．

探索思路：如上图，∵BC=Kab,k=1，∴BC=AB．

∴∠CAB=∠ACB．

∵m∥n，∴∠MAC=∠ACB．

添加条件：∠ABC=90°．

证明：如图，在直线m上截取AM=AB，连结ME．

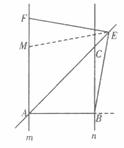
∵BC=kAB,k=1，∴BC=AB．∵∠ABC=90°, ∴∠CAB=∠ACB=45°,

∵m∥n，∴∠MAE=∠ACB=∠CAB=45°, ∠FAB=90°．

∵AE=AE, ∴△MAE≌△ABE．

∴EM=EB, ∠AME=∠ABE．

∵∠BEF=∠ABC=90°, ∴∠FAB+∠BEF=180°．

∴∠ABE+∠EFA=180°,又∵∠AME+∠EMF=180°,

∴∠EMF=∠EFA．

∴EM=EF． ∴EF=EB．

(2)EF=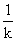EB．

说明：如图，过点E作EM⊥m、EN⊥AB,垂足为M、N．

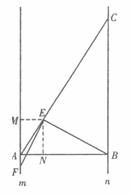
∴∠EMF=∠ENA=∠ENB=90°．

∵m∥n，∠ABC=90°, ∴∠MAB=90°．

∴四边形MENA为矩形．∴ME=NA, ∠MEN=90°．

∵∠BEF=∠ABC=90°． ∴∠MEF=∠NEB．

∴△MEF∽△NEB．

∴∴

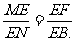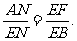
在Rt△ANE和Rt△ABC中，tan∠BAC=，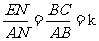

∴EF=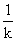EB．

6.[答案]：(1)①CF与BD位置关系是 垂直、数量关系是相等；

②当点D在BC的延长线上时①的结论仍成立．

由正方形ADEF得　 AD=AF ，∠DAF=90º．

∵∠BAC=90º，∴∠DAF=∠BAC ，　 ∴∠DAB=∠FAC，

又AB=AC ，∴△DAB≌△FAC　 ， ∴CF=BD　 　　

　 ∠ACF=∠ABD．

∵∠BAC=90º， AB=AC ，∴∠ABC=45º，∴∠ACF=45º，

∴∠BCF=∠ACB+∠ACF= 90º．即 CF⊥BD

(2)画图正确　　　　

当∠BCA=45º时，CF⊥BD(如图丁)．

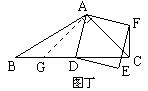
理由是：过点A作AG⊥AC交BC于点G，∴AC=AG

可证：△GAD≌△CAF　 ∴∠ACF=∠AGD=45º　

∠BCF=∠ACB+∠ACF= 90º．　 即CF⊥BD

(3)当具备∠BCA=45º时，

过点A作AQ⊥BC交BC的延长线于点Q，(如图戊)

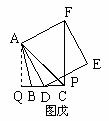
∵DE与CF交于点P时， ∴此时点D位于线段CQ上，

∵∠BCA=45º，可求出AQ= CQ=4．设CD=x ，∴　 DQ=4-x，

容易说明△AQD∽△DCP，∴ ，　 ∴，．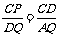

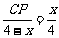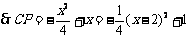∵0＜x≤3　 ∴当x=2时，CP有最大值1．

5.[答案]解：(1)任选两个三角形的所有可能情况如下六种情况：①②，①③，①④，②③，②④，③④其中有两组(①③，②④)是相似的．

∴选取到的二个三角形是相似三角形的概率是P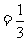

(2)证明：选择①、③证明．

在△AOB与△COD中,　∵AB∥CD,

∴∠CDB＝∠DBA　,　∠DCA＝∠CAB,

∴△AOB∽△COD

选择②、④证明.

∵四边形ABCD是等腰梯形, ∴∠DAB＝∠CAB,

∴在△DAB与△CBA中有

AD=BC, ∠DAB＝∠CAB,AB=AB,

∴△DAB ≌ △CBA,

∴∠ADO＝∠BCO.

又∠DOA＝∠COB, ∴△DOA∽△COB