4.[解析]考察了相似的两种基本图形，平行四边形中利用全等三角形的简单证明.

[答案](1) AEH与DFH．(或AEH与BEG， 或BEG与CFG ，或DFH与CFG)

(2)OE=OF．

证明：四边形ABCD是平行四边形，

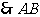∥CD，　 ，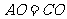

，　△△，　　　　

．

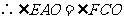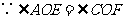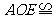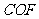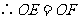3.[解析]由于A、C、E三点共线可证明三角形ACD与三角形BCE全等(边角边)从而可证AD=BE、∠AOB=∠CAD+∠CEB=∠CCBE+∠CEB =∠ACB= 60°，再证三角形ACP全等于三角形BCQ，从而可证AP=BQ，PQ∥AE。如果DE=DP，那么就会有DE=DP=EQ(三角形CEQ全等于三角形CDP)EQ=CE因为∠DCE=60°，所以三角形CEQ为等边三角形，矛盾。

[答案](1)(2)(3)(5)

2.[解析]由本题图形相似已经有一个公共角，再找一组对应角相等或公共角的两边对应成比例即可。

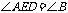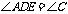[答案] ，或，或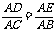

1.[解析]由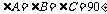可知四边形ABCD是矩形,再得到正方形方法有很多,比如邻边相等、对角线互相垂直等。答案不唯一。

[答案] AB=BC或者BC=CD或者CD=DA或者DA=AB

7．(·大连市)点A、B分别是两条平行线m、n上任意两点，在直线n上找一点C，使BC = kAB，连结AC，在直线AC上任取一点E，作∠BEF =∠ABC，EF交直线m于点F．

⑴如图1，当k = 1时，探究线段EF与EB的关系，并中以说明；

说明：①如果你经过反复探索没有解决问题，请写出探索过程(要求至少写三步)；

②在完成①之后，可以自己添加条件(添加的条件限定为∠ABC为特殊角)，在图2中补全图形，完成证明．

⑵如图3，若∠ABC = 90°，k≠1，探究线段EF与EB的关系，并说明理由．

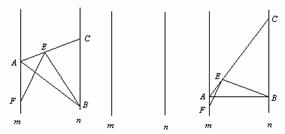
图1　　　　　　 图2　　　　　　　　 图3

第3课时　 开放探究题 答案

6.(·盐城)如图甲，在△ABC中，∠ACB为锐角．点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．解答下列问题：

(1)如果AB=AC，∠BAC=90º．

①当点D在线段BC上时(与点B不重合)，如图乙，线段CF、BD之间的位置关系为　　 ，数量关系为　　　 ．

②当点D在线段BC的延长线上时，如图丙，①中的结论是否仍然成立，为什么？

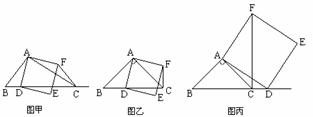
(2)如果AB≠AC，∠BAC≠90º，点D在线段BC上运动．试探究：当△ABC满足一个什么条件时，CF⊥BC(点C、F重合除外)？画出相应图形，并说明理由．(画图不写作法)

(3)若AC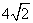＝，BC=3，在(2)的条件下，设正方形ADEF的边DE与线段CF相交于点P，求线段CP长的最大值．

类型之四　 综合型问题

　 这类问题是指条件、结论、解题方法都不全或未知，而仅提供一种问题情境，需要我们补充条件，设计结论，并寻求解法的一类问题；它更具有开发性，能为我们提供宽松的思维环境，解这类题时，要求我们对课本知识特别熟悉并能灵活运用。

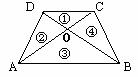
5.(•常德市)如图，在梯形ABCD中，若AB//DC，AD=BC，对角线BD、AC把梯形分成了四个小三角形．

　 (1)列出从这四个小三角形中任选两个三角形的所有可能情况，并求出选取到的两个三角形是相似三角形的概率是多少(注意：全等看成相似的特例)？

　 (2)请你任选一组相似三角形，并给出证明．

类型之三　 策略开放型问题

策略开放型也称为设计方案型，是指题目的条件和结论都已知或部分已知，需要探索解题方法或设计解题方案的一类试题；这种类型的开放性试题的处理方法一般需要模仿、类比、试验、创新和综合运用所学知识，建立合理的数学模型，从而使问题得以解决。策略开放性问题的解题方法一般不惟一或解题路径不明确，要求解题者不墨守成规，善于标新立异，积极发散思维，优化解题方案和过程。

4.(•梅州)如图，四边形ABCD是平行四边形．O是对角线AC的中点，过点O的直线EF分别交AB、DC于点E、F，与CB、AD的延长线分别交于点G、H．

(1)写出图中不全等的两个相似三角形(不要求证明)；

(2)除AB=CD，AD=BC，OA=OC这三对相等的线段外，图中还有多对相等的线段，请选出其中一对加以证明．

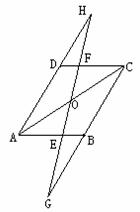
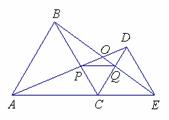
3.(•滨州市)如上右图，C为线段AE上一动点(不与点A，E重合)，在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ.以下五个结论：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP；⑤∠AOB=60°.恒成立的结论有_________(把你认为正确的序号都填上)。

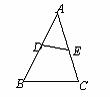
2.(•庆阳市)如下左图，D、E分别是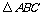的边AB、AC上的点，则使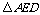∽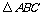的条件是　　　 ．

类型之二　 结论开放型问题

解决这种类型的问题的时候要充分利用已知条件或图形特征，进行猜想、归纳、类比，透彻分析出给定条件下可能存在的结论现象，然后经过论证作出取舍，这是一种归纳类比型思维. 它要求解题者充分利用条件进行大胆而合理的猜想，发现规律，得出结论，这类题主要考查解题者的发散性思维和所学基本知识的应用能力。