
4. (2009温州)如图,△ABC中,∠C=90°,AB=8,cosA=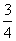 ,则AC的长是
;
,则AC的长是
;
3. (2009宁波)如图,在坡屋顶的设计图中,AB=AC,屋顶的宽度l为10米,坡角α这35°,则坡屋顶的高度h为
米.(结果精确到0.1米)
2.
(2009益阳)如图3,先锋村准备在坡角为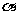 的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为
的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为
A. 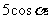 B.
B. 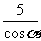
C. 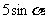 D.
D. 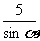
1.
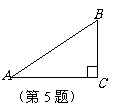 (2009湖州)如图,在
(2009湖州)如图,在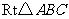 中,
中,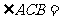
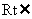 ,
,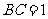 ,
,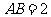 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.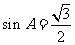 B.
B.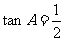
C.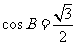 D.
D.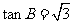
21.[解析](Ⅰ)
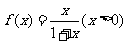 .则
.则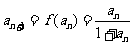 ,得
,得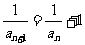 ,即
,即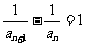 ,
,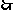 数列
数列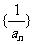 是以2为首项、1为公差的等差数列,故
是以2为首项、1为公差的等差数列,故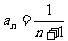 .(4分)
.(4分)
(Ⅱ)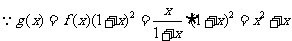 ,
,
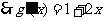 ,即在点
,即在点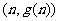
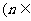 N*)处切线的斜率
N*)处切线的斜率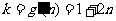 ,
,
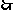 切线方程为
切线方程为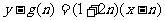 ,令
,令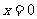 ,得
,得
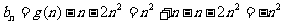 .(9分)
.(9分)
(Ⅲ)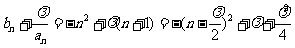 ,仅当
,仅当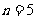 时取最大值,只需
时取最大值,只需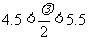 ,解得
,解得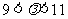 .故
.故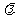 的取值范围为
的取值范围为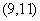 .(14分)
.(14分)
[链接高考] 本题是函数、数列、导数等的大型综合题,衔接自然,叙述流畅,毫无拼凑的痕迹,情景新颖,具有较好的区分度,入口较宽.要求学生具有一定的审题、读题能力,一定的等价变形能力,要求学生具有较高的数学素养和数学灵气.
数列综合题和立体几何以及解析几何大题,每年出现,年年有变化.因此,对数列综合题应进行系统探究,思考数列可能与哪些分支的知识综合考查.不过,数列与不等式的综合,是一种比较常见的题型,不可忽视.尤其数列不等式采用导数工具来处理的新题不可小视.
20.[解析](Ⅰ)因为函数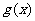 的图象经过原点,所以
的图象经过原点,所以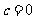 ,则
,则
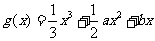 .
.
根据导数的几何意义知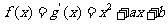 ,………4分
,………4分
由已知-2、4是方程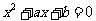 的两个实数,
的两个实数,
由韦达定理,
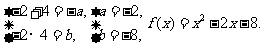 …………6分
…………6分
(Ⅱ)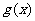 在区间[-1,3]上是单调减函数,所以在[-1,3]区间上恒有
在区间[-1,3]上是单调减函数,所以在[-1,3]区间上恒有
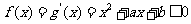 ,即
,即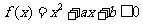 在[-1,3]恒成立,
在[-1,3]恒成立,
这只需满足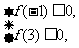 即可,也即
即可,也即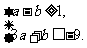 …………10分
…………10分
而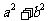 可视为平面区域
可视为平面区域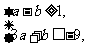 内的点到原点距离的平方,其中点(-2,-3)距离原点最近,所以当
内的点到原点距离的平方,其中点(-2,-3)距离原点最近,所以当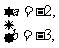 时,
时, 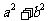 有最小值13. …………14分
有最小值13. …………14分
[链接高考]自从导数走进高考试题中,就和函数形影不离,并且与方程、数列、解析几何以及立体几何等分支的知识联姻,成为高考的一道亮丽的风景线.预计导数还会与平面向量、概率与统计等分支的知识联合,展示其独特的魅力.
19. [证明]由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=DC. ……4分
(Ⅰ)连接DB,可知B、N、D共线,且AC⊥DN.
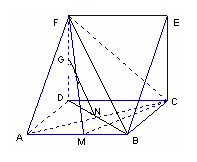 又FD⊥AD FD⊥CD,
又FD⊥AD FD⊥CD,
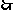 FD⊥面ABCD.
FD⊥面ABCD.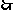 FD⊥AC.
FD⊥AC.
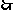 AC⊥面FDN
AC⊥面FDN 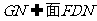 .
.
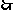 GN⊥AC. ……9分
GN⊥AC. ……9分
(Ⅱ)点P在A点处.
证明:取DC中点S,连接AS、GS、GA.
 G是DF的中点,
G是DF的中点,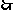 GS//FC,AS//CM.
GS//FC,AS//CM.
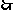 面GSA//面FMC,
面GSA//面FMC, ,
,
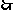 GA//面FMC,即GP//面FMC. ……14分.
GA//面FMC,即GP//面FMC. ……14分.
[链接高考]本题主要考查直三棱柱的有关知识,以及求直线与平面所成的角的问题,以及分析问题与解决问题的能力.简单几何体是立体几何解答题的主要载体,特别是棱柱和棱锥.由于棱锥已多次出现在高考试题中,估计今年高考会以棱柱为载体来命题.
18. [解析](Ⅰ)由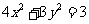 得,
得,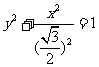 ,
,
所以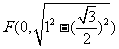 ,即
,即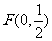 .
.
则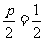 ,即
,即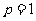 ,故抛物线方程为
,故抛物线方程为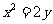 ,即
,即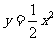 .
.
由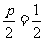 知,
知, 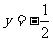 是抛物线
是抛物线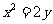 的准线,故
的准线,故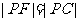 .
.
假设存在点P,使△PCF为等腰直角三角形,则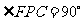 ,即
,即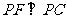 ,而
,而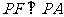 .故
.故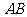 与
与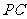 重合,即
重合,即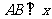 轴,这与直线AB不垂直x轴矛盾.因此,不存在点P,使△PCF为等腰直角三角形.
轴,这与直线AB不垂直x轴矛盾.因此,不存在点P,使△PCF为等腰直角三角形.
(Ⅱ)设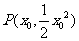 ,
,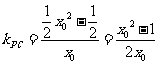 ,由
,由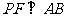 知,
知, 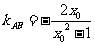 ,则
,则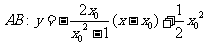 .
.
令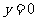 得,
得, 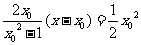 ,即
,即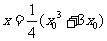 ,
,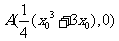 ,
,
令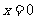 得,
得, 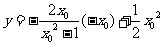 ,即
,即
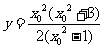 ,
,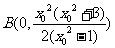 .…10分
.…10分
若P平分线段AB,则有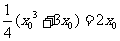 且
且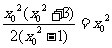 ,
,
解得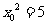 ,即
,即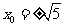 .
.
故存在点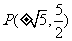 ,使P平分线段AB. …………………13分
,使P平分线段AB. …………………13分
[链接高考] 圆锥曲线的综合大题, 主要考查解析几何的有关知识,以及分析问题与解决问题的能力.除了2004年出现了两道大题(其中有一题以圆锥曲线的应用题形式出现)外,基本上是每年一道大题.除了2006年以函数的面貌,基本上还是以常态的形式出现,即以直线与圆锥曲线的位置关系的形式出现.值得引起重视的一个现象是,经常出现一条或几条直线与两种圆锥曲线(包括圆)的位置关系问题,同时要注意其与平面向量以及导数的知识的综合命题.
17.[解析](Ⅰ)考生总人数是50,因此表中标出的总人数也应是50,所以a +b+ c+ 40=50,
故a +b+ c =50-40=10; …………………………3分
(Ⅱ)从表中可以看出,“政治成绩为4分且英语成绩为3分”的考生人数为6人,所以其概率为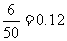 .
……………………………8分
.
……………………………8分
(Ⅲ)因为若“考生的政治成绩为4分” 与“英语成绩为2分”是相互独立事件,
所以P(x=4,y=2)= P(x=4)·P(y=2),即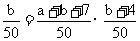 ,
,
解得: b=1,a=2,c=7. …………………………………13分
[链接高考]概率与统计的综合题,自从2005年走进新高考试题中,就以崭新的姿态,在高考中占有极其重要的地位,每年出现一道大题.开始两年文理合卷,考查的是随机变量的分布列和数学期望问题.2007年文理开始分卷,2007年考查的是统计中的线性回归方程,2008年考查的统计中的分层抽样和概率问题,预计这是概率与统计大题的命题趋势,这类题基本上是中档题,预计还有可能与函数、导数、方程、数列以及不等式等知识综合考查.
16.[解析]本题要用到数量积的坐标形式,以及一个重要的三角恒等式:
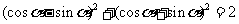 .
.
(Ⅰ)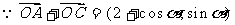 ,
,
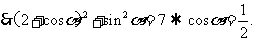
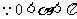 ,
,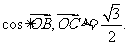
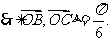 ………4分
………4分
(Ⅱ)(解法一)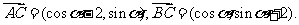
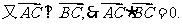
 .
.
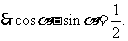 ①
………8分
①
………8分
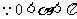 ,
,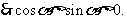
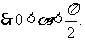
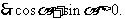
由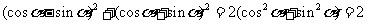 ,得
,得
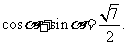 ②
②
由①、②联立解方程组得
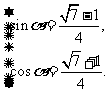
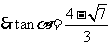 .
………12分
.
………12分
(解法二)由解法一知,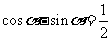 ,且
,且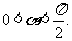
将上式平方得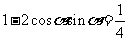 ,即
,即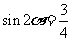 .
.
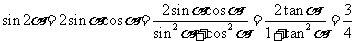 ,解得
,解得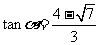 .
.
[链接高考]处理三角函数与平面向量的综合题,通常利用向量的数量积等知识,将向量问题转化为三角函数问题来处理.考查综合能力,转化与化归思想,以及分析问题和解决问题的能力.
解决本题的关键是,利用两个向量的数量积的坐标形式,将向量问题转化为三角函数问题来处理.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com