
3.组合数公式的推导
⑴提问:从4个不同元素a,b,c,d中取出3个元素的组合数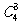 是多少呢?
是多少呢?
启发: 由于排列是先组合再排列,而从4个不同元素中取出3个元素的排列数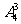 可以求得,故我们可以考察一下
可以求得,故我们可以考察一下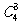 和
和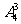 的关系,如下:
的关系,如下:
组 合 排列
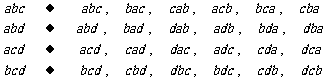
由此可知:每一个组合都对应着6个不同的排列,因此,求从4个不同元素中取出3个元素的排列数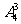 ,可以分如下两步:① 考虑从4个不同元素中取出3个元素的组合,共有
,可以分如下两步:① 考虑从4个不同元素中取出3个元素的组合,共有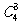 个;② 对每一个组合的3个不同元素进行全排列,各有
个;② 对每一个组合的3个不同元素进行全排列,各有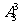 种方法.由分步计数原理得:
种方法.由分步计数原理得: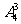 =
=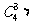
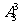 ,所以:
,所以: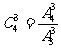 .
.
⑵ 推广: 一般地,求从n个不同元素中取出m个元素的排列数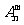 ,可以分如下两步:① 先求从n个不同元素中取出m个元素的组合数
,可以分如下两步:① 先求从n个不同元素中取出m个元素的组合数 ;② 求每一个组合中m个元素全排列数
;② 求每一个组合中m个元素全排列数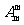 ,根据分布计数原理得:
,根据分布计数原理得: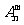 =
=

⑶ 组合数的公式:
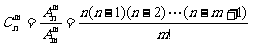
或 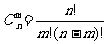

⑷ 巩固练习:
2.组合数的概念:从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数.用符号 表示.
表示.
例如:示例2中从3个同学选出2名同学的组合可以为:甲乙,甲丙,乙丙.即有 种组合.
种组合.
又如:从A、B、C、D四个景点选出2个进行游览的组合:AB,AC,AD,BC,BD,CD一共6种组合,即: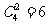
在讲解时一定要让学生去分析:要解决的问题是排列问题还是组合问
题,关键是看是否与顺序有关.
那么又如何计算 呢?
呢?
1.组合的概念:一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.
注:1.不同元素 2.“只取不排”--无序性 3.相同组合:元素相同
判断下列问题哪个是排列问题哪个是组合问题:
⑴ 从A、B、C、D四个景点选出2个进行游览;(组合)
⑵ 从甲、乙、丙、丁四个学生中选出2个人担任班长和团支部书记.(排列)
2.提出问题:
示例1: 从甲、乙、丙3名同学中选出2名去参加某天的一项活动,其中1名同学参加上午的活动,1名同学参加下午的活动,有多少种不同的选法?
示例2: 从甲、乙、丙3名同学中选出2名去参加一项活动,有多少种不同的选法?
引导观察:示例1中不但要求选出2名同学,而且还要按照一定的顺序“排列”,而示例2只要求选出2名同学,是与顺序无关的.
引出课题:组合问题.
1.复习排列的有关内容:
|
|
定 义 |
特 点 |
相同排列 |
公 式 |
|
排 列 |
|
|
|
|
|
|
|
|
|
|
以上由学生口答.
3、数列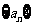 的首项
的首项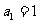 ,前
,前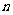 项和为
项和为 ,满足关系式:
,满足关系式: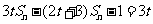 ,
,
(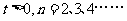 )。
)。
求证:数列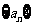 是等比数列。
是等比数列。
数列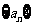 的公比为
的公比为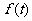 ,作数列
,作数列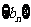 ,
,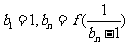 ,
, ,求
,求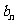 。
。
2、函数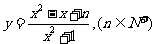 ;
;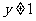 的最小值为
的最小值为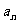 ,最大值为
,最大值为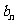 ,且
,且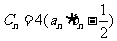 ,求数列
,求数列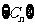 的前
的前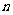 项和
项和 ,
,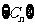 的通项公式。
的通项公式。
1.设数列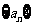 和
和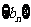 满足
满足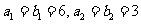 ,且数列
,且数列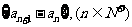 是等差数列,数列
是等差数列,数列 是等比数列,求
是等比数列,求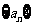 与
与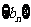 的通项公式。
的通项公式。
5、过圆 内一点P
内一点P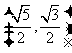 有
有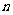 条弦的长度成等差数列
条弦的长度成等差数列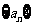 ,如果过P点的圆的最短的弦长为
,如果过P点的圆的最短的弦长为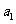 ,最长的弦长为
,最长的弦长为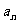 ,且公差为
,且公差为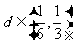 ,则
,则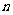 的取值集合为( )
的取值集合为( )
A、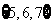 B、
B、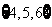 C、
C、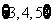 D、
D、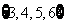 三。能力训练:
三。能力训练:
例1、求数列的通项公式:
①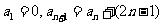 ;(
;(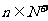 )
)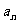 =
=
②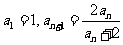 ,(
,(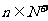 )
)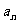 =
。
=
。
③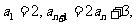
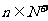 ,则
,则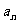 =
。
=
。
④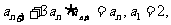 则
则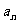 =
。
=
。
⑤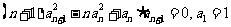 ,
,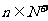 ,
,
则 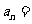 。
。
⑥设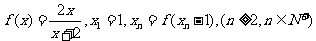 ,则
,则
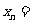 。
。
⑦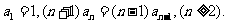 ;则
;则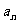 =
=
例2:求数列的通项公式:
①数列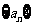 ,
,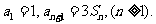 则
则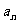 =
=
②已知 ,则
,则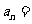 。
。
③数列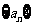 的前
的前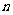 项和为
项和为 ,
,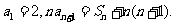 则
则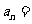 。
。
④数列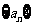 中,
中,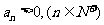 ,前
,前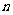 项和
项和 与通项
与通项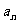 满足关系关系式
满足关系关系式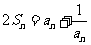 , 求
, 求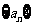 的通项公式。
的通项公式。
例3.
①数列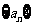 中,
中,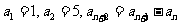 ,(
,(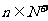 ),则
),则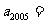 。
。
②数列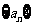 中,
中,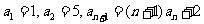 , 则
, 则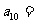 。
。
③数列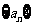 满足
满足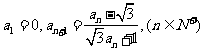 ,则
,则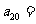 。
。
④已知数列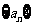 中,
中,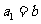 (
(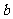 为正常数),
为正常数),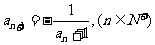 ,能使
,能使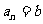 的
的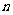 的值是( )
的值是( )
A、14 B、15 C、16 D、17
⑤若数列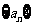 的前8项的值各异,且
的前8项的值各异,且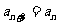 对任意
对任意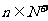 都成立,则下列数列中可取遍
都成立,则下列数列中可取遍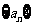 前8项值的数列为( )
前8项值的数列为( )
A、 B、
B、 C、
C、 D、
D、
4、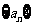 等差,
等差,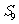 =18,
=18, =240,
=240, ,则
,则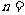 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com