
(二)选做题(14-15题,考生只能从中选做一题)
14.(坐标系与参数方程选做题)[解析]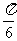 或
或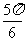 .设直线的点斜式方程为
.设直线的点斜式方程为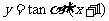 ,圆的普通方程是
,圆的普通方程是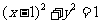 ,由直线与圆相切知,
,由直线与圆相切知, 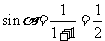 , 因
, 因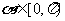 ,则
,则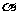 =
=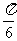 或
或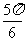 .
.
[链接高考]本小题主要考查直线的点斜式方程与圆的极坐标方程的有关知识,以及转化与化归的思想方法.解决本题的关键是将它们转化为直角坐标系下的直线与圆的交点问题来处理.
15.(几何证明选讲选做题)[解析]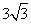 .设等腰梯形的底角为
.设等腰梯形的底角为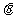 ,则由图可知,
,则由图可知, ,即
,即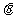 =
=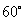 .
由
.
由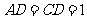 知,
知,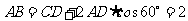 ,故梯形的面积为
,故梯形的面积为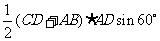
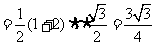 ,故平行四边形的面积为
,故平行四边形的面积为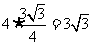 .
.
[链接高考]本小题主要考查梯形与平行四边形的有关知识,以及分析问题和解决问题的能力,以及转化与化归的思想方法.
(一)必做题(11-13题)
11.[解析]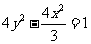 .设双曲线方程为
.设双曲线方程为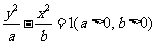 .由
.由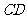 中点的纵坐标为1知,梯形的中位线长为1,即
中点的纵坐标为1知,梯形的中位线长为1,即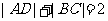 ,结合
,结合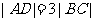 ,解得
,解得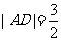 ,则
,则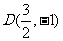 在双曲线上,则
在双曲线上,则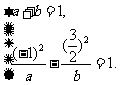 解得
解得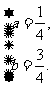
[链接高考]命题意图:主要考查平面几何和双曲线的方程极其性质,以及分析问题和解决问题的能力.
12.[解析]4.设正三棱锥的高为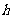 ,底面正三角形的边长为
,底面正三角形的边长为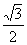 ,
,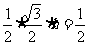 ,
,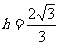 .
.
这个棱锥的侧面与底面所成角的正切值=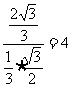 .
.
[链接高考]有关简单的几何体的小题在高考中始终保持一定的比例,应熟练掌握.
13.[解析]100、200.设公司在甲电视台和乙电视台做广告的时间分别为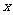 分钟和
分钟和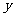 分钟,总收益为
分钟,总收益为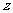 元,由题意得
元,由题意得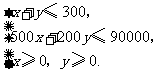
 即
即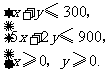 目标函数为
目标函数为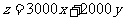 .
.
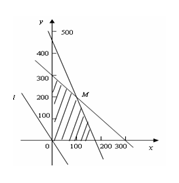
作出二元一次不等式组所表示的平面区域,即可行域.如图:作直线 ,即
,即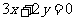 .
.
平移直线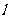 ,从图中可知,当直线
,从图中可知,当直线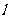 过
过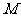 点时,目标函数取得最大值.由
点时,目标函数取得最大值.由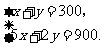
得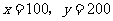 .
.
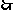 点
点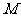 的坐标为
的坐标为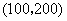 .
. 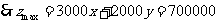 (元)
(元)
[链接高考]本题是一道有关椭圆与双曲线的归纳类比题,这类题的特点是:往往并不需要证明结论,主要考查考生的创新精神,是否会观察,会抽象概括,会用类比的方法得出新的一般性的结论. 这类题目经常出现在高考试题中,经常以数列或解析几何等知识为载体.
10.[解析]B.可按照大人带小孩的方式进行分类:当1个大人带2个小孩坐甲游艇时有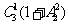 =9种坐法, 当2个大人各带1个小孩坐甲游艇时有
=9种坐法, 当2个大人各带1个小孩坐甲游艇时有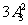 =18种坐法,因此,总共有9+18=27种坐法.
=18种坐法,因此,总共有9+18=27种坐法.
[链接高考]自从概率与统计走进高考试题后,排列与组合应用题时隐时现,但不是不考,而是与概率与统计综合考查,当然有时也单独命题.
9.[解析]C.由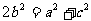 得,
得,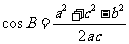
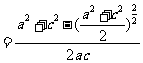
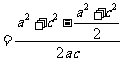
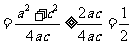 ,得到
,得到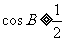 ,
,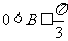 .
.
[链接高考]本题是三角函数的有关知识与不等式的综合.不等式作为一种工具,经常与其它知识综合考查.
8.[解析]C.注意到从球刚开始露出水面到球整个离开水面过程中,球露出水面的部分体积等于圆柱容器水面下降的体积,由于球是匀速拉出水面的,拉出水面体积的变化率先增大再减小,故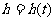 图象切线的斜率先减小后增大,故选C.
图象切线的斜率先减小后增大,故选C.
[链接高考]本小题是具有物理背景的一道小型综合题,主要考查有关导数和立体几何的有关知识,以及分析问题和解决问题的能力.
7.[解析]A.设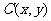 满足条件
满足条件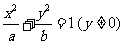 ,则
,则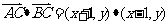
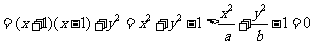 .选
.选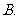
[链接高考]本题主要考查椭圆、平面向量、不等式及充要条件等知识,是一道较综合的小题.
6.[解析]D.设点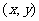 在
在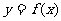 的图像上,则
的图像上,则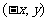 在
在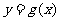 的图像上,即
的图像上,即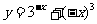 ,也即
,也即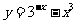 .
.
[链接高考]本题是有关函数的对称性问题的综合题.对称问题是高考中的重要内容,经常与其它知识综合考查.
5.[解析]B. 将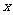 的取值
的取值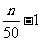 记
记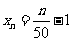 ,相应的
,相应的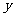 值记为
值记为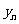 .则
.则 ,即
,即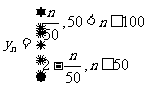 故
故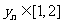 .
.
[链接高考]本小题主要考查选择语句知识和数列知识,以及分析问题和解决问题的能力. 算法初步是高考新增的考点.近两年每年都有一道小题,常与数列等知识进行小综合来考查,估计以后的考查形式不会有大的变化.
4.[解析]A.抽出的人数为:0.0005×500×100=25,选A.
[链接高考]本小题主要考查样本的频率分布直方图的知识和分析问题以及解决问题的能力. 统计初步在近两年高考中每年都以小题的形式出现,基本上是低起点题.
3.[解析]B.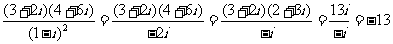 .
.
[链接高考]本题是一道复数的简单代数运算问题.有关复数的考查,最近五年只是一道选择题,主要考查复数的基本概念和复数的简单运算.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com