
2. 已知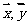 不共线,且
不共线,且 ,其中
,其中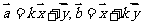 ,则实数
,则实数 的值为_________ .
的值为_________ . 
1. 设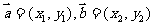 ,则
,则 的充要条件是(
C ).
的充要条件是(
C ).
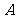
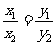
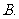
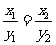
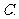
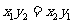
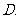 以上都不对
以上都不对
17. 已知三角形的重心为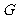 ,过
,过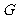 作直线
作直线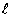 分别交边
分别交边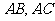 于
于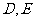 ,且
,且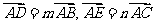 .
.
设⊿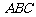 ,⊿
,⊿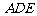 的面积分别为
的面积分别为 .
.
(1)求证: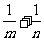 为定值,并求出该定值;
为定值,并求出该定值;
(2)求证: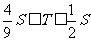 .
.
3 优化作业本,P73,P31;中学1+1,P81
16. 已知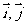 分别是
分别是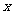 轴、
轴、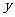 轴正方向上的单位向量,
轴正方向上的单位向量,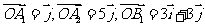 ,且
,且
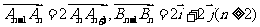 .
.
(1)求: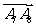 ; (2)求
; (2)求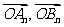 的坐标 .
的坐标 . 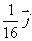 ;
;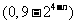 ,
,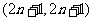
15. 设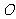 为平面内任意一点,
为平面内任意一点, 为不同的两点,则点
为不同的两点,则点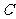 在直线
在直线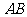 上的充要条件是:
上的充要条件是:
存在实数 ,使得
,使得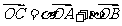 ,且
,且 . 特别地,点
. 特别地,点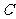 在线段
在线段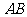 上的充要
上的充要
条件是:存在非负实数 ,使得
,使得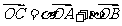 ,且
,且 .
.
优化作业本,P77,P33
14. 过原点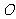 的直线与
的直线与 的图象交于
的图象交于 两点,过
两点,过 分别作
分别作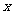 轴的垂线分别交
轴的垂线分别交
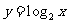 的图象于
的图象于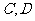 两点,求证:
两点,求证: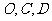 三点在同一条直线上 .
三点在同一条直线上 .
13. 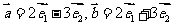 ,其中
,其中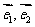 为不共线的非零向量.
为不共线的非零向量. 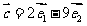 .
.
问是否存在实数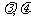 ,
,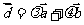 与
与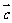 共线 . 存在,
共线 . 存在,
12.
已知点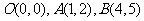 及
及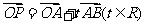 ,
,
求:(1)t为何值时,P在x轴上?P在y轴上?P在第二象限?
(2)四边形OABP能否成为平行四边形?若能,求出相应的t值;若不能,请说明理由.
解:(1)∵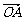 =(1,2),
=(1,2),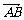 =(3,3), ∴
=(3,3), ∴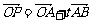 =(1+3t,2+3t).
=(1+3t,2+3t).
当P在x轴上时,有2+3t=0,即t=- ; 当P在y轴上时,有1+3t=0,即t=-
; 当P在y轴上时,有1+3t=0,即t=-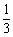 ;
;
当P在第二象限时,有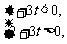 即-
即- <t<-
<t<-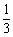 .
.
(2)∵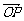 =(1+3t,2+3t),
=(1+3t,2+3t),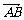 =(3,3),假如OABP能成为平行四边形,则有
=(3,3),假如OABP能成为平行四边形,则有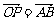 ,
,
即(1+3t,2+3t)=(3,3),∴有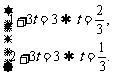 该方程组无解,
该方程组无解,
∴假设不成立. ∴四边形不能成为平行四边形.
11. 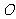 是平面上的一个定点,
是平面上的一个定点,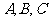 是平面上不共线的三个点,动点
是平面上不共线的三个点,动点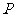 满足:
满足:
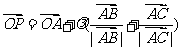 ,
,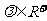 ,则动点
,则动点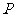 的轨迹一定通过
的轨迹一定通过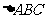 的 ( A
).
的 ( A
).
A.内心 B.外心 C.重心 D.垂心
10. 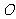 是平面上的一个定点,
是平面上的一个定点,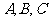 是平面上不共线的三个点,动点
是平面上不共线的三个点,动点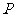 满足:
满足:
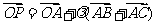 ,
,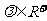 ,则动点
,则动点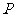 的轨迹一定通过
的轨迹一定通过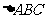 的( C ).
的( C ).
A.内心 B.外心 C.重心 D.垂心
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com