
(二)能力训练点
1.理解并掌握两个平面平行的定义.
2.掌握两个平面的位置关系应用了类比的方法,体现了分类的数学思维方法.
3.会画平行或相交平面的空间图形,并用字母或符号表示,进一步培养学生的空间想象能力.
4.掌握两个平面的判定定理的证明,进一步培养学生严密的逻辑思维能力.
(一)知识教学点
1.两个平面平行的定义.
2.两个平面的位置关系及画法.
3.两个平面平行的判定.
22、(10分)二次函数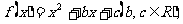 不论
不论 为何实数
为何实数 且
且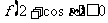 .
.
⑴求证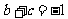 ;⑵求证
;⑵求证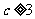 ⑶若函数
⑶若函数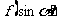 的最大值是
的最大值是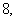 求
求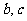 .
.
20、(14分)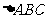 是
是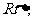
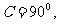 内角
内角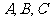 所对边为
所对边为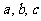 .求:
.求:
⑴若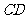 是斜边
是斜边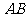 上的中线,用向量法证明
上的中线,用向量法证明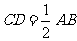 ;
;
⑵若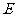 为
为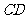 中点,连结
中点,连结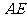 并延长
并延长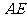 交
交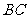 于
于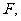 求
求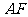 的长度(用
的长度(用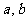 表示).
表示).
 21、(12分)我炮兵阵地位于地面
21、(12分)我炮兵阵地位于地面 处,两观察所分别位于地面点
处,两观察所分别位于地面点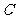 和
和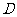 处,已知
处,已知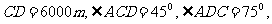 且目标出现在地面B处时,测得
且目标出现在地面B处时,测得 .求:炮兵阵地到目标的距离.
.求:炮兵阵地到目标的距离.
19、(12分)已知函数 的定义域为
的定义域为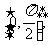 值域
值域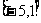 .求常数
.求常数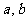 的值.
的值.
18、(14分)若向量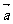 的始点为
的始点为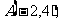 终点
终点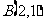 求:
求:
⑴向量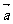 的模长;⑵与
的模长;⑵与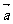 平行的单位向量
平行的单位向量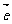 的坐标;⑶与
的坐标;⑶与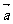 垂直的单位向量
垂直的单位向量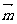 的坐标.
的坐标.
17、(12分)已知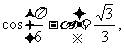 求
求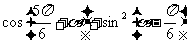 的值.
的值.
16、已知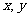 都是锐角
都是锐角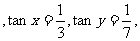 则
则 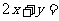 .
.
15、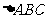 中,若三内角
中,若三内角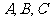 成等差数列,三边
成等差数列,三边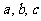 成等比数列
成等比数列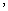 且
且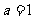 ,则
,则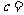 .
.
14、锐角三角形三边分别为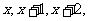 且最大内角不超过
且最大内角不超过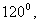 则
则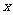 的取值范围是 .
的取值范围是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com