
1、抛物线 y=-x2+1 的开口向____.
21.解:(Ⅰ)由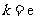 得
得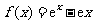 ,所以
,所以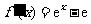 .
.
由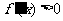 得
得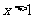 ,故
,故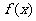 的单调递增区间是
的单调递增区间是 ,
,
由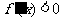 得
得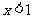 ,故
,故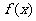 的单调递减区间是
的单调递减区间是 .……………………………4分
.……………………………4分
(Ⅱ)由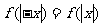 可知
可知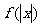 是偶函数.
是偶函数.
于是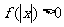 对任意
对任意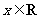 成立等价于
成立等价于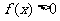 对任意
对任意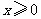 成立.
成立.
由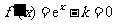 得
得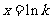 .
.
①当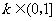 时,
时, .
.
此时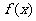 在
在 上单调递增.
上单调递增.
故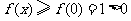 ,符合题意.
,符合题意.
②当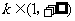 时,
时,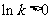 .
.
当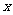 变化时
变化时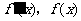 的变化情况如下表:
的变化情况如下表:
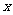 |
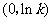 |
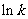 |
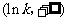 |
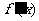 |
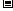 |
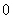 |
 |
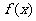 |
单调递减 |
极小值 |
单调递增 |
由此可得,在 上,
上,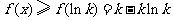 .
.
依题意,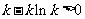 ,又
,又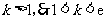 .
.
综合①,②得,实数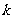 的取值范围是
的取值范围是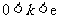 .……………………………9分
.……………………………9分
(Ⅲ)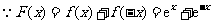 ,
,
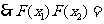
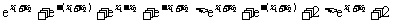 ,
,
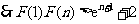 ,
,

由此得,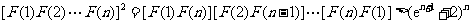
故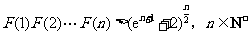 .……………………………14分
.……………………………14分
[链接高考]自从导数走进高考试题中,就和函数形影不离,并且与方程、不等式、数列、解析几何以及立体几何等分支的知识联姻,成为高考的一道亮丽的风景线.预计导数还会与平面向量、概率与统计等分支的知识联合,展示其独特的魅力.
20.解:(Ⅰ)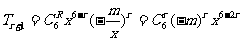 ,因6-2r=0,得r=3;
,因6-2r=0,得r=3;
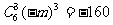 得m=2.………………………………………3分
得m=2.………………………………………3分
(Ⅱ)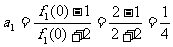 ,
,
 ,
,
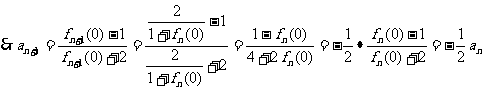 ,
,
则数列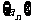 是以
是以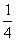 为首项,-
为首项,-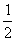 为公比的等比数列.
为公比的等比数列.
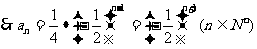 ,…………………………………7分
,…………………………………7分
(Ⅲ)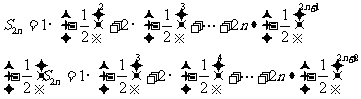
两式相减得: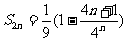 ,
,
又 ,
,
比较9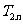 与
与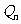 的大小,就是比较
的大小,就是比较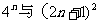 的大小:
的大小:

……………………10分
下面用数学归纳法证明: (1)当n=3时显然成立;
(1)当n=3时显然成立;
(2)设当n=k时猜想成立,即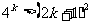 ,
,
那么当n=k+1时,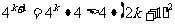 ,
,
又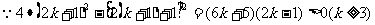 ,
,
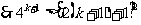 ,
,
所以当n=k+1时猜想也成立.
综上所述:对于一切大于3的正整数都有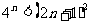 .
.
所以,当n=1、2时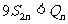 ,当
,当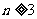 时,
时,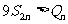 .……………14分
.……………14分
[链接高考]数列综合题和立体几何以及解析几何大题,每年出现,年年有变化.因此,对数列综合题应进行系统探究,思考数列可能与哪些分支的知识综合考查.不过,数列与不等式的综合,是一种比较常见的题型,不可忽视.尤其数列不等式采用分类和数学归纳法等工具来处理的新题不可小视.
19.解:(Ⅰ)由题意得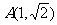 ,设
,设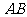 的斜率为
的斜率为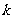 ,则
,则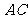 的斜率为-
的斜率为-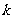 ,
,
所以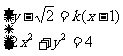 ,代入得
,代入得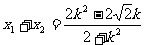 ,又
,又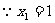 ,
,
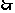
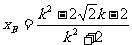 ; 同理
; 同理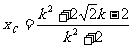 .
.
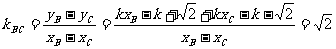 为定值.……………………8分
为定值.……………………8分
(Ⅱ)设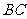 方程为
方程为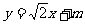 , 由
, 由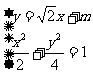 得
得
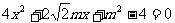 ,得
,得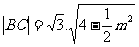 ,
,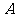 到
到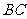 的距离为
的距离为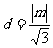 ;
;
所以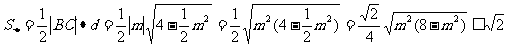 .
.
当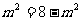 时,即
时,即 时“=”成立,此时
时“=”成立,此时 成立.……………………14分
成立.……………………14分
[链接高考]圆锥曲线的综合大题, 主要考查解析几何的有关知识,以及分析问题与解决问题的能力.基本上是每年一道大题.主要是以直线与圆锥曲线的位置关系的形式出现.考查学生基本方法和基本运算,值得引起重视的一个现象是字母多的运算,同时要注意其与平面向量以及导数的知识的综合命题.
18.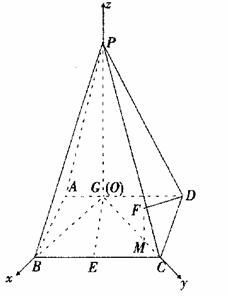 ]解法一:(I)由已知
]解法一:(I)由已知
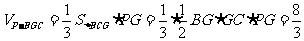
∴PG=4;
如图所示,以G点为原点建立空间直角坐标系
o-xyz,则
B(2,0,0),C(0,2,0),P(0,0,4),
故E(1,1,0);
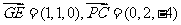 ,
,
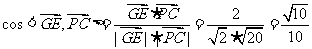 ,
,
∴异面直线GE与PC所成的角的余弦值为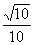 .……………………4分
.……………………4分
(II)平面PBG的单位法向量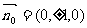 ,
,
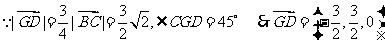 ,
,
∴点D到平面PBG的距离为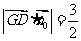 .……………………8分
.……………………8分
(III)设F(0,y , z),
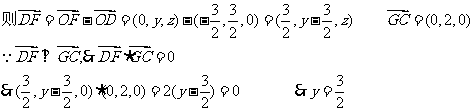
在平面PGC内过F点作FM⊥GC,M为垂足,则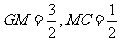 ,
,
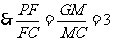 .……………………14分
.……………………14分
解法二:
(I)由已知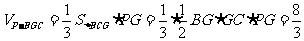 ,
,
∴PG=4.
在平面ABCD内,过C点作CH//EG交AD于H,连结PH,则∠PCH(或其补角)就是异面直线GE与PC所成的角.
在△PCH中,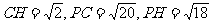 ,
,
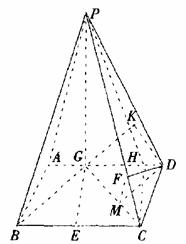 由余弦定理得,cos∠PCH=
由余弦定理得,cos∠PCH=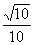 ,
,
∴异面直线GE与PC所成的角的余弦值为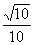 .
.
(II)∵PG⊥平面ABCD,PG 平面PBG ∴平面PBG⊥平面ABCD,
平面PBG ∴平面PBG⊥平面ABCD,
在平面ABCD内,过D作DK⊥BG,交BG延长线于K,
则DK⊥平面PBG ∴DK的长就是点D到平面PBG的距离.
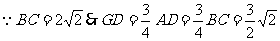 .
.
在△DKG,DK=DGsin45°=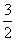 , ∴点D到平面PBG的距离为
, ∴点D到平面PBG的距离为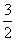 .
.
(III)在平面ABCD内,过D作DM⊥GC,M为垂足,连结MF,又因为DF⊥GC,
∴GC⊥平面MFD, ∴GC⊥FM.
由平面PGC⊥平面ABCD,∴FM⊥平面ABCD ∴FM//PG;
由GM⊥MD得:GM=GD·cos45°=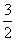 .
.
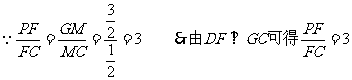 ,
,
∴x=,解得d=∈(0,).
[链接高考]本题主要考查四棱锥的有关知识,以及求异面直线所成角的问题,以及分析问题与解决问题的能力.简单几何体是立体几何解答题的主要载体,特别是棱柱和棱锥.
17.解:(Ⅰ)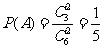 ;……………………4分
;……………………4分
(Ⅱ)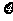 的可能值为1,2,3,4,
的可能值为1,2,3,4,
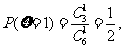
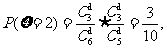
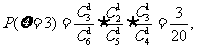
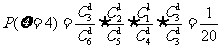 . ……………………8分
. ……………………8分
∴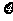 的分布列为
的分布列为
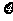 |
1 |
2 |
3 |
4 |
|
P |
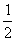 |
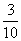 |
 |
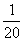 |
故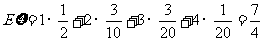 . ……………………12分
. ……………………12分
[链接高考]概率与统计的综合题,自从2005年走进新高考试题中,就以崭新的姿态,在高考中占有极其重要的地位,每年出现一道大题.除了2007年考查的是统计中的线性回归方程外,有三年考查的是随机变量的分布列和数学期望问题.这是概率与统计大题考查的主阵地,预计还有可能与函数、导数、方程、数列以及不等式等知识综合考查.
16.解:(Ⅰ)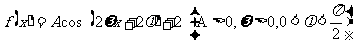 ,
,
依题意 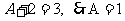 . ……………………1分
. ……………………1分
又  ;
; 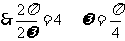 ……………………3分
……………………3分
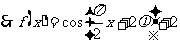 .
.
令 x=0,得 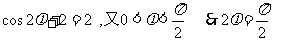 ,
,
所以, 函数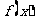 的解析式为
的解析式为 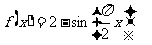 . ……………………6分
. ……………………6分
(Ⅱ)由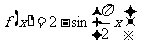 知
知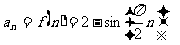 ,
,
当n为偶数时,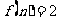 ;……………………9分
;……………………9分
当n为奇数时,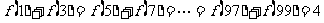 ,
,
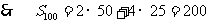 . …………………12分
. …………………12分
[链接高考]本小题主要考查三角函数的图象和性质,又巧妙与数列结合起来,运用了分类讨论等数学思想方法.
(二)选做题(13-15题,考生只能从中选做两题)
13.2.[解析]曲线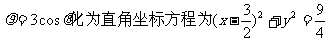 表示圆,直线
表示圆,直线
 ,由图形知圆心到直线的距离为
,由图形知圆心到直线的距离为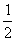 ,所以圆上的点到直线的最大距离为
,所以圆上的点到直线的最大距离为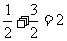 .
.
[链接高考]坐标系与参数方程是选修内容之一,有时考极坐标,有时考参数方程,有时两内容结合一起。
14.4.[解析]利用柯西不等式得 .
.
[链接高考]不等式选讲中主要是三个正数的均值不等式、含有绝对值的不等式和柯西不等式等内容.
15.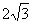 .[解析]由
.[解析]由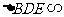
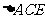 得
得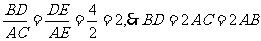 ,在
,在 中,AD=6,由勾股定理可求得AB=
中,AD=6,由勾股定理可求得AB=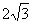 .
.
[链接高考]几何证明选讲中主要有平行成比例、相似三角形、圆中的直径、角、弦、切线等知识.
(一)必做题(9-12题)
9.1、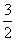 、2、
、2、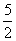 .[解析]第一个输出的数是1;第二个输出的数是
.[解析]第一个输出的数是1;第二个输出的数是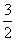 ;第三个输出的数是2;第四个输出的数是
;第三个输出的数是2;第四个输出的数是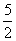 .
.
[链接高考]算法初步是高考新增的考点.近两年每年都有一道小题,常与函数、数列等知识进行小综合来考查,估计以后的考查形式不会有大的变化.
10.2.6.[解析]点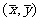 在回归直线上,计算得
在回归直线上,计算得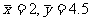 代入得a=2.6.
代入得a=2.6.
[链接高考]统计也是高考新增的考点,07年高考有一大题,不要忘记了.
11.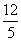 .[解析]画出可行域,由
.[解析]画出可行域,由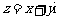 得
得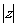 =
=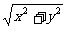 知其几何意义为原点与可行域内点之间的距离,从而得到最小值为
知其几何意义为原点与可行域内点之间的距离,从而得到最小值为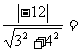
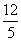 .
.
[链接高考]线性规划主要考查动手能力,与其他知识的结合重点在于问题的转化.
12.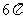 .[解析]由三视图可知这几何体是棱长为2的正四面体,它的外接球的直径是棱长为
.[解析]由三视图可知这几何体是棱长为2的正四面体,它的外接球的直径是棱长为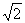 的正方体的对角线
的正方体的对角线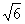 ,球的表面积为
,球的表面积为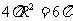 .
.
[链接高考]三视图是新增内容,近几年高考都有考,有大题也有小题,立几中正方体是基本的几何模型,要重点掌握.
8.B.[解析]由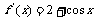
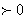 ,f(0)=0得f(x)在(-1,1)上单调递增和
,f(0)=0得f(x)在(-1,1)上单调递增和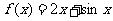 ,从而得f(x)是奇函数;所以f(1-x)
,从而得f(x)是奇函数;所以f(1-x)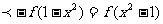 即有
即有 解得
解得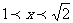 故选B.
故选B.
[链接高考]函数、导数、不等式的综合问题是代数中常见的问题,综合性强,主要考查推理能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com