
(三). 抽样问题
例1. 有13名医生, 其中女医生6人, 现从中抽调5名医生组成医疗小组前往灾区, 若医疗小组至少有2名男医生, 同时至多有3名女医生, 则不同选派方法有 ( )种.
A.  B.
B.  C.
C.  D.
D. 
例2: 集合 和集合
和集合 各含有10个元素,
各含有10个元素,  含有4个元素. 试求同时满足下列两个条件的集合
含有4个元素. 试求同时满足下列两个条件的集合 的个数. (1)
的个数. (1)  , 且
, 且 只含有3个元素; (2)
只含有3个元素; (2)  .
.
例3: 从52张扑克牌中任取5张, 问有3张花样不同点值相同, 另外两张点值不同的取法有多少种?
(二). 捆、插、序排、错排问题
例1: 现有 、
、 、
、 、
、 、
、 、
、 、
、 、
、 8位同学站成一排照相. 要求同学
8位同学站成一排照相. 要求同学 、
、 相邻,
相邻,  、
、 相邻, 而
相邻, 而 、
、 不相邻. 这样的排队照相方式有
种.
不相邻. 这样的排队照相方式有
种.
例2: 身穿红、黄两种颜色衣服的各有2人, 穿蓝色衣服的有1人. 现将5人排成一行. 要求穿相同颜色衣服的人不能相邻. 则不同的排法共有 种.
例3: (1)原节目单上有8个节目, 现新插入3个节目, 则不同插法的种数为 .
(2)在某次数学考试中, 学号为 的同学的考试成绩
的同学的考试成绩 , 且满足
, 且满足 . 则这4位同学的考试成绩的所有可能情况有几种? 若
. 则这4位同学的考试成绩的所有可能情况有几种? 若 , 则有多少种可能情况?
, 则有多少种可能情况?
例4: 7个人坐成一排, 现要调换其中4个人中的一个人的位置, 其余3个人的位置不变, 则不同的调换方式有 种. 若调换位置的过程中, 保证至少3个人位置不变, 则不同的调换方式有 种.
(一). 计数原理
例1: 已知集合 这三个集合中各取一个元素构成空间直角坐标系中点的坐标, 则确定的不同点的个数有 个.
这三个集合中各取一个元素构成空间直角坐标系中点的坐标, 则确定的不同点的个数有 个.
例2: 设集合 , 选择
, 选择 的两个非空子集
的两个非空子集 和
和 , 要使
, 要使 中最小的数大于
中最小的数大于 中最大的数, 则不同的选择方式共有
个.
中最大的数, 则不同的选择方式共有
个.
排列、组合问题的常见解题方法有:
(1)特殊元素(特殊位置)优先安排法;
(2)合现分类与准确分步法;
(3)排列、组合混合问题先选后排法;
(4)相邻问题捆绑处理法;
(5)不相邻问题插空处理法;
(6)定序问题除法处理;
(7)分排问题直排处理法;
(8)“小集团”排列问题先整体后局部法;
(9)构造模型处理法;
(10)正难则反, 等价转化法.
 例1.(1)已知定义在
例1.(1)已知定义在 上的奇函数
上的奇函数 满足
满足 ,则
,则 = _________.
= _________.
(2)设 的最小正周期
的最小正周期 且
且 为偶函数,
为偶函数,
它在区间 上的图象如右图所示的线段
上的图象如右图所示的线段 ,则在区间
,则在区间 上,
上,
 ________
________
(3)已知函数 是周期为
是周期为 的函数,当
的函数,当 时,
时, ,
,
当 时,
时, 的解析式是________
的解析式是________
例2;定义在 上的函数
上的函数 ,对任意
,对任意 ,有
,有 ,且
,且 ,
, 求证:
求证: ;
;  判断
判断 的奇偶性;
的奇偶性;
 若存在非零常数
若存在非零常数 ,使
,使 ,①证明对任意
,①证明对任意 都有
都有 成立;②函数
成立;②函数 是不是周期函数,为什么?
是不是周期函数,为什么?
五当堂检测
 已知函数
已知函数 是以
是以 为周期的周期函数,且当
为周期的周期函数,且当 时,
时, ,则
,则
 =________
=________
 设偶函数
设偶函数 对任意
对任意 ,都有
,都有 ,且当
,且当 时,
时,
 ,则
,则 ________
________
 设函数
设函数 是定义在
是定义在 上的奇函数,对于任意的
上的奇函数,对于任意的 ,都有
,都有 ,当
,当 ≤
≤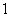 时,
时, ,则
,则 ________
________
4.已知 是定义在实数集
是定义在实数集 上的函数,满足
上的函数,满足 ,且
,且 时,
时, .
. 求
求 时
时 的表达式;
的表达式; 证明
证明 是
是 上的奇函数.
上的奇函数.
4.
2(09江西文)函数 的最小正周期为_________.
的最小正周期为_________.
3.(09山东理)已知定义在R上的奇函数 ,满足
,满足 ,且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间
,且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间 上有四个不同的根
上有四个不同的根 ,则
,则
2.(09山东文)已知定义在R上的奇函数 ,满足
,满足 ,且在区间[0,2]上是增函数,则f(-25),f(11),f(80)的大小关系是_________.
,且在区间[0,2]上是增函数,则f(-25),f(11),f(80)的大小关系是_________.
1.(09山东卷理)定义在R上的函数f(x)满足f(x)=  ,则f(2009)的值为_________.
,则f(2009)的值为_________.
4.主要方法:
( )判断一个函数是否是周期函数要抓住两点:一是对定义域中任意的
)判断一个函数是否是周期函数要抓住两点:一是对定义域中任意的 恒有
恒有 ;
;
二是能找到适合这一等式的非零常数 ,一般来说,周期函数的定义域均为无限集.
,一般来说,周期函数的定义域均为无限集.
( )解决周期函数问题时,要注意灵活运用以上结论,同时要重视数形结合思想方法的运用,还要注意根据所要解决的问题的特征来进行赋值。
)解决周期函数问题时,要注意灵活运用以上结论,同时要重视数形结合思想方法的运用,还要注意根据所要解决的问题的特征来进行赋值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com