
4.在电影院内,如果将“12排4号”记作(12,4),那么“3排6号”应表示为( )
A.(3,6) B.(6,3) C.(4,12) D.6号3排
3.已知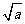 +
+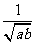 有意义,则点P(a,-b)关于原点的对称点在( )
有意义,则点P(a,-b)关于原点的对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
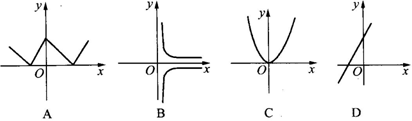
2.如图的四个图象中,不表示某一函数图象的是( )
1.当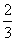 <m<1时,点P(3m-2,m-1)在(
)
<m<1时,点P(3m-2,m-1)在(
)
A.第一象限 B.第二象限 C.第三象限 D.第四象限
21. 解:(1) 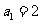 ,
,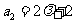 ,
,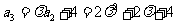 .
…………1分
.
…………1分
① 若数列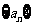 为等差数列,则
为等差数列,则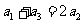 ,即
,即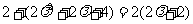 ,得
,得
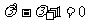 ,由
,由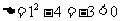 知方程无实根,
知方程无实根,
故不存在实数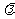 ,使得数列
,使得数列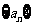 为等差数列.
…………3分
为等差数列.
…………3分
② 若数列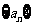 为等比数列,则
为等比数列,则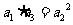 ,即
,即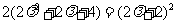 ,解得
,解得
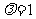 ,此时,
,此时,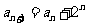 ,由累加法得:
,由累加法得:
 ,
,
显然,当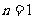 时也适合,故
时也适合,故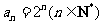 .
.
故存在实数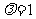 ,使得数列
,使得数列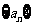 为等比数列,其通项公式为
为等比数列,其通项公式为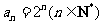 .
…………6分
.
…………6分
(2)① 当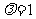 时,
时,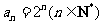 ,故
,故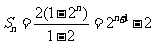 .
…………7分
.
…………7分
② 当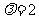 时,
时,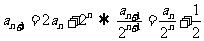 ,即数列
,即数列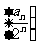 是首项为
是首项为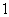 ,公差为
,公差为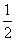 的等差数列,故
的等差数列,故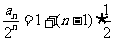 ,即
,即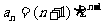 ,下用错位相减法求
,下用错位相减法求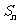 .
.
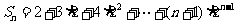 ,
,
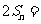
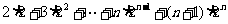 ,
,
上面两式相减,得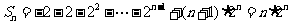 .
…………10分
.
…………10分
③ 当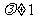 且
且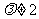 时,下用待定系数法求通项
时,下用待定系数法求通项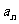 .
.
令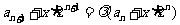 ,则
,则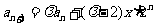 ,
,
上式与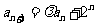 比较系数,得
比较系数,得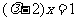 ,
,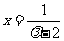 .
.
故数列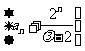 是首项为
是首项为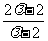 ,公比为
,公比为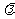 的等比数列,从而
的等比数列,从而
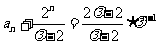 ,即
,即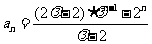 .
.
因此,
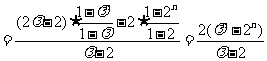 .
.
综上所述,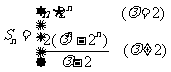 .
…………14分
.
…………14分
[链接高考] 本题是一道数列综合题,情景熟悉,貌似简单,入手也不难,但综合程度之高令人叹为观止.无论是分类讨论的思想,还是反证推理、求数列通项和数列求和都考查得淋漓尽致,累加法和待定系数法求数列的通项、错位相减法和分组求和法求数列的前 项和,几乎数列的所有知识和方法都熔于一炉.
项和,几乎数列的所有知识和方法都熔于一炉.
20. 解:(1) 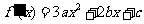 ,
…………1分
,
…………1分
由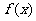 在
在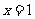 处取得极值,得
处取得极值,得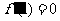 ,即
,即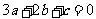 ,
…………2分
,
…………2分
由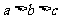 知:
知: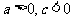 .
.
由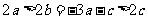 ,得
,得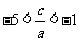 ①.
…………3分
①.
…………3分
曲线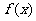 在
在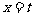 处的切线斜率为
处的切线斜率为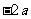 ,得
,得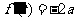 ,即
,即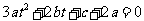 .
.
由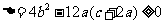 ,将
,将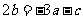 代入,得
代入,得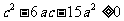 ,
,
即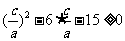 ,解得:
,解得: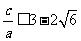 或
或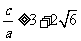 ②.
…………5分
②.
…………5分
由①②联立得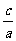 的取值范围是
的取值范围是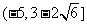 .
…………6分
.
…………6分
(2)由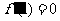 知:方程
知:方程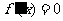 即
即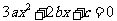 的一根为1,设另一根为
的一根为1,设另一根为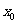 ,则
,则
由韦达定理,得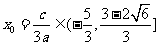 .
.
由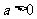 ,令
,令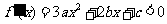 ,得
,得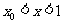 ,则
,则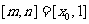 ,从而
,从而
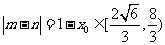 ,故
,故 的最小值为
的最小值为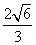 .
…………10分
.
…………10分
(3)由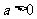 知,当
知,当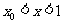 时
时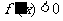 ;当
;当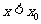 或
或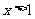 时
时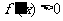 .
.
而 ,则
,则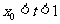 ,于是
,于是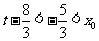 ,故
,故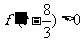 ,即
,即
曲线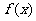 在
在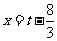 处的切线斜率为正.
…………14分
处的切线斜率为正.
…………14分
[链接高考]本题是一道从三个“二次”即二次函数、二次方程和二次不等式的相互关系演变而来的代数推理题. 三次函数与二次函数联系紧密,因为将三次函数求导就转化为二次函数. 此题以导数的几何意义为载体,巧妙地将导数与函数、方程与不等式等知识综合交汇在一起,对逻辑推理能力的考查达到极致,确实是一道好题.
19. 解:(1) 设椭圆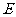 的方程为
的方程为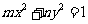 (
(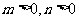 ),
…………1分
),
…………1分
将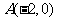 、
、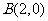 、
、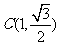 代入,得
代入,得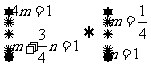 .
…………3分
.
…………3分
∴椭圆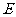 的方程为
的方程为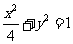 .
…………4分
.
…………4分
(2)当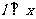 轴时,
轴时,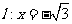 ,易得
,易得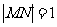 ,则
,则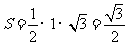 .
…………5分
.
…………5分
当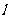 的斜率存在时,设
的斜率存在时,设 :
: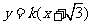 ,代入椭圆方程
,代入椭圆方程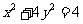 ,得
,得
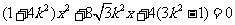 ,
,
,m设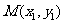 ,
,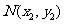 ,则
,则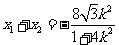 ,
,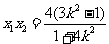 . …………6分
. …………6分
∵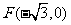 为椭圆
为椭圆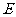 的左焦点,
的左焦点,
∴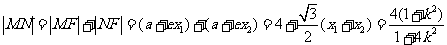 .
…………8分
.
…………8分
又原点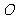 到直线
到直线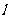 的距离
的距离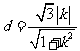 ,
…………9分
,
…………9分
∴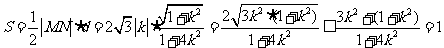 .
………12分
.
………12分
上式等号当且仅当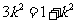 ,即
,即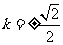 时成立. …………13分
时成立. …………13分
综上,Δ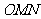 的面积
的面积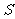 的最大值为1,此时直线
的最大值为1,此时直线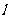 的方程为
的方程为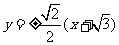 即
即
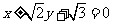 .
…………14分
.
…………14分
[链接高考]本题考查用待定系数法求曲线方程以及直线和圆锥曲线的位置关系,综合性强,字母运算能力是一大考验,灵活运用均值不等式求三角形面积的最值是一大难点.
18. (1) 证明:连结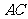 交
交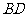 于点
于点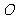 ,连结
,连结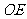 ,
,
∵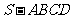 是正四棱锥,
是正四棱锥,
∴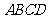 是正方形,∴
是正方形,∴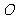 是
是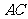 的中点.
的中点.
∵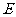 是侧棱
是侧棱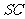 的中点,∴
的中点,∴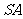 ∥
∥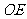 ,
,
又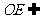 平面
平面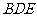 ,
,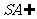 平面
平面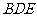 ,
,
∴直线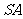 ∥平面
∥平面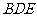 . …………4分
. …………4分
(2)
解:∵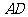 ∥
∥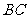 ,
,
∴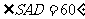 为异面直线
为异面直线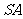 和
和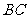 所成的角,△
所成的角,△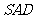 是等边三角形.
是等边三角形.
根据正棱锥的性质得,△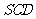 、△
、△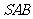 、△
、△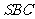 也是等边三角形.
也是等边三角形.
连结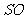 ,取
,取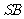 中点
中点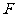 ,连结
,连结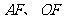 ,
,
∵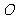 是正方形
是正方形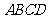 的中心,根据正棱锥的性质得,
的中心,根据正棱锥的性质得,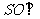 平面
平面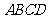 ,
,
∴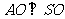 ,又
,又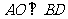 ,∴
,∴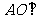 平面
平面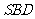 .
.
∵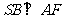 ,根据三垂线定理的逆定理,得
,根据三垂线定理的逆定理,得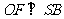 ,
,
∴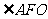 是二面角
是二面角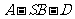 的平面角.
的平面角.
RtΔ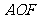 中,
中,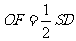 ,
,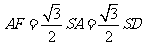 ,
,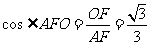 ,
,
∴二面角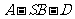 的余弦值是
的余弦值是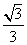 .
…………9分
.
…………9分
(3) 解:∵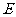 是侧棱
是侧棱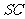 的中点,∴
的中点,∴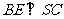 ,
,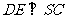 ,∴
,∴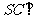 平面
平面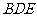 ,
,
∴平面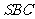 ⊥平面
⊥平面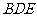 ,过
,过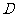 作平面
作平面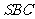 的垂线,垂足在交线
的垂线,垂足在交线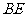 上,
上,
即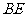 为
为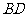 在平面
在平面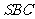 上的射影,∴
上的射影,∴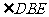 为直线
为直线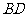 和平面
和平面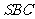 所成的角,
所成的角,
∵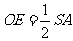 ,
,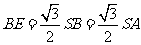 ,
,
∴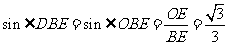 ,
,
∴线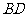 和平面
和平面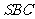 所成的角的正弦值为
所成的角的正弦值为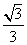 .
…………14分
.
…………14分
[链接高考] 本题综合考查空间中线线、线面的位置关系和空间中角的计算,涉及线线角、线面角和二面角的平面角,传统方法和坐标向量法均可,考查的知识面较广,难度中等,值得一做.
17. 解:(1)因为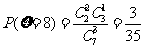 ,
…………1分
,
…………1分
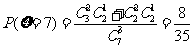 ,
…………3分
,
…………3分
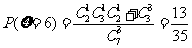 ,
…………5分
,
…………5分
所以线路信息通畅的概率为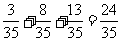 .
…………6分
.
…………6分
(2) 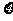 的所有可能取值为4,5,6,7,8.
…………7分
的所有可能取值为4,5,6,7,8.
…………7分
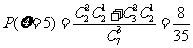 ,
…………9分
,
…………9分
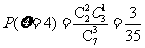 .
…………10分
.
…………10分
∴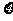 的分布列为
的分布列为
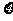 |
4 |
5 |
6 |
7 |
8 |
|
P |
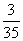 |
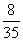 |
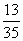 |
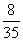 |
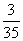 |
…………11分
∴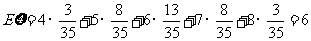 .
…………13分
.
…………13分
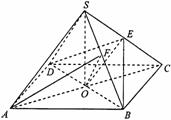 [链接高考]概率统计的综合题,难度不大,因此一直是广大考生力求拿分的重要项目. 概率、期望的
[链接高考]概率统计的综合题,难度不大,因此一直是广大考生力求拿分的重要项目. 概率、期望的
计算是经常考查的内容,排列、组合知识是基础,掌握准确的分类和分步是解决概率问题的奠基石.
16. 解:(1)依题意,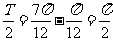 ,即
,即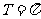 ,故
,故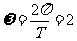 .
…………1分
.
…………1分
由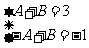 ,解得
,解得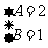 .
…………3分
.
…………3分
把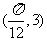 代入
代入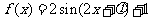 ,得
,得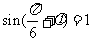 ,
,
又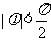 ,故
,故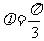 .
…………5分
.
…………5分
综上所述,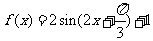 .
…………6分
.
…………6分
(2) 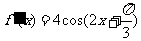 .
…………8分
.
…………8分
由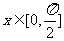 ,得
,得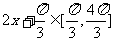 ,则
,则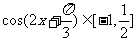 ,
…………10分
,
…………10分
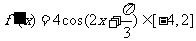 ,
…………11分
,
…………11分
故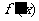 在区间
在区间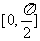 上的最大值为2,最小值为
上的最大值为2,最小值为 .
…………12分
.
…………12分
[链接高考]本题主要考查三角函数的图象和性质,融会了待定系数法求函数解析式和三角复合函数求导等知识,是一道比较基础的中档题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com