
2.4分段函数求值
必备知识:
2.求值域的常用方法:
(1)
换元法 形如: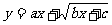 求值域
求值域
(2)
判别式法 形如: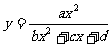 求值域,去分母转换为一元二次方程,由
求值域,去分母转换为一元二次方程,由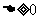 求出y的范围
求出y的范围
(3)
分离常数法 形如: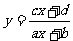 求值域
求值域
(4) 反函数法 利用互为反函数定义域和值域互换的特点,原函数值域就是反函数定义域。
(5) 数形结合法 如:三角函数、含绝对值的函数
(6)
均值不等式 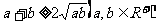
例题讲解:
例题1(09福建模拟)函数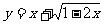 的值域是( )B
的值域是( )B
A. B.
B.
 C.R
D.
C.R
D. 
练习1:求函数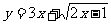 的值域.
的值域.
例题2(08重庆文)函数f(x)=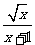 的最大值为( B )
的最大值为( B )
A.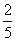 B.
B.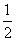 C.
C.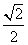 D.1
D.1
练习2:(09东北模拟)函数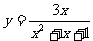 其中(x<0)的值域( )A
其中(x<0)的值域( )A
A. B.
B.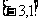 C.
C. D.
D.
例题3求函数(09湖北文)函数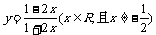 的值域是
的值域是 ( )B
( )B
A.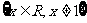 B.
B. 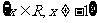 C.
C.  D.
D. 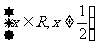
练习3:求函数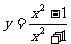 的值域.
的值域.
例题4(08四川模拟)函数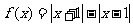 的值域是
.
的值域是
.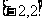
练习4求函数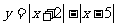 的值域是
.
的值域是
.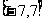
例题5函数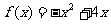 在
在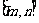 上的值域是
上的值域是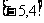 ,则
,则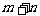 的取值范围是( )D
的取值范围是( )D
A. B.
B.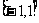 C.
C.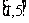 D.
D.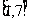
练习5:已知函数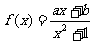 的值域为
的值域为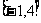 ,求实数
,求实数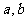 的值.
的值.
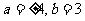
1.定义:函数值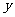 的取值范围叫做函数的值域.
的取值范围叫做函数的值域.
2.3求函数值域
课程引入:
初中一次函数图像引入,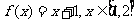 ,
,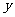 的取值范围?图像处理
的取值范围?图像处理
必备知识:
3. 求函数的定义域即转化为解不等式(组),可用“区间”或“集合”来表示.
例题讲解:
例题1(08全国1文)函数 的定义域为( )D
的定义域为( )D
A.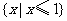 B.
B.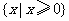 C.
C. D.
D.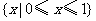
练习1:(09江西文)函数 的定义域为
的定义域为
 ( )D
( )D
A.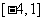 B.
B.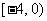 C.
C.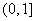 D.
D.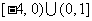


例题2(08江西文)若函数 的定义域是
的定义域是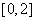 ,则函数
,则函数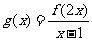 的定义域是( )B
的定义域是( )B
A.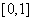 B.
B.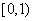 C.
C.
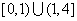 D.
D.
练习2:若函数 的定义域是
的定义域是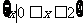 ,则函数
,则函数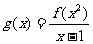 的定义域为( )A
的定义域为( )A
A.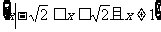 B.
B.
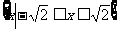
C.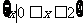 D.
D.
例题3函数 的定义域为R,则
的定义域为R,则 的取值范围是
.
的取值范围是
.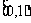
练习3:已知函数 的定义域为R,求
的定义域为R,求 的取值范围
.
的取值范围
.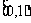
例题4若函数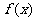 的定义域为
的定义域为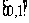 ,求
,求 的定义域.
的定义域.
练习4:若函数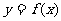 的定义域是
的定义域是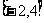 ,则函数
,则函数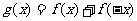 的定义域是( )B
的定义域是( )B
A.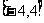 B.
B.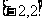 C.
C.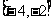 D.
D.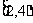
2. 常见函数定义域:(1)分母不为零(2)对数真数大于零(3)开偶次根式,被开方数大于或等于零
1. 定义:自变量x的取值范围(映射观点:原象的集合)
2.2求函数定义域
课程引入:
函数 ,求其定义域.
,求其定义域.
必备知识:
2.
函数定义:对于数集A中任何一个元素在数集B中都有唯一的元素与之对应,那么这样的对应叫做集合A到集合B的函数,记作: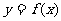 ,自变量
,自变量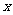 的取值范围叫做定义域,函数值
的取值范围叫做定义域,函数值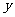 的取值范围叫做值域,
的取值范围叫做值域,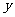 与
与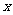 之间的关系叫做对应法则。
之间的关系叫做对应法则。
例题讲解:
例题1(06湖北模拟)设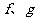 都是由A到A的映射,其对应法则如下表(从上到下):
都是由A到A的映射,其对应法则如下表(从上到下):
表1 映射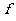 的对应法则
的对应法则
|
原象 |
1 |
2 |
3 |
4 |
|
象 |
3 |
4 |
2 |
1 |
表2 映射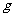 的对应法则
的对应法则
|
原象 |
1 |
2 |
3 |
4 |
|
象 |
4 |
3 |
1 |
2 |
则与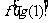 相同的是( )A
相同的是( )A
A.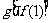 B.
B. 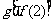 C.
C. D.
D. 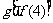
练习1(07北京模拟)设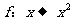 是集合A到集合B的映射,如果
是集合A到集合B的映射,如果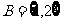 ,则
,则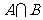 等于( )C
等于( )C
A.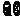 B.
B.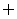 C.
C. 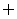 或
或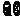 D.
D. 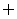 或
或
例题2已知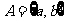 ,
,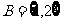 ,则映射
,则映射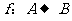 的个数为
。4
的个数为
。4
练习2: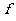 是从集合
是从集合 到集合
到集合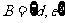 的映射,则满足映射条件的“
的映射,则满足映射条件的“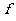 ”共有( )D
”共有( )D
A.5个 B.6个 C.7个 D.8个
例题3已知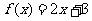 ,求
,求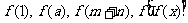 .
.
练习3已知 ,求
,求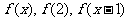
1.
映射的定义:对于集合A中任何一个元素在集合B中都有唯一的元素与之对应,那么这样的对应叫做集合A到集合B的映射,记作: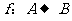 ,其中A中的元素叫做原象,B中的元素叫做象,
,其中A中的元素叫做原象,B中的元素叫做象,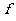 叫做对应关系(或对应法则)。
叫做对应关系(或对应法则)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com