
向量数量积的物理模型是力的做功,两个非零向量夹角的范围是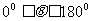 ,平面向量的数量积是一个实数。
,平面向量的数量积是一个实数。
平面向量的数量积是向量的一种新的运算,它的定义、法则和性质不同于以往的运算,它是从物理中的“求功运算”中抽象出来的,从数、式的运算到向量的运算,是运算的一次飞跃。
导学训练
教科书第81页习题2.4第1,2,3题
例1 判断下列说法是否正确:
① 向量的数量积可以是任意实数。
②
若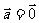 ,则对任意向量
,则对任意向量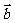 ,有
,有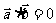 。
。
③
若 ,则对任意非零向量
,则对任意非零向量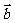 ,有
,有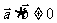 。
。
④
如果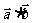 >0,那么
>0,那么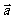 与
与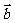 的夹角为锐角。
的夹角为锐角。
⑤
若 ,
,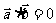 ,则
,则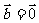 。
。
⑥
若 ,
,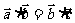 ,则
,则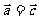 。
。
例2 已知向量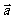 与
与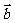 的夹角为
的夹角为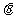 ,
,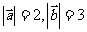 ,分别在下列条件下求
,分别在下列条件下求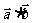 :
:
(1)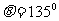 ;(2)
;(2)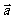 ∥
∥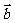 ;(3)
;(3)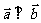
(直接应用)
例3 已知正△ABC的边长为2,设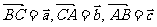 ,求
,求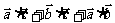
变式:在平行四边形ABCD中,已知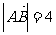 ,
,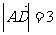 ,
,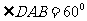 ,求:
,求:
(1)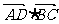 ;(2)
;(2)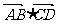 ;(3)
;(3)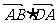
问题 从求功的运算中,可以抽象出什么样的数学运算?(学生讨论)
平面向量的数量积
(1)最初的认识
学生讨论:如把力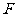 和位移
和位移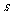 抽象地看成两个“向量”,把力
抽象地看成两个“向量”,把力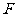 与位移
与位移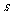 的夹角
的夹角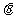 抽象地看成两个向量的夹角,就可以得到一种新的运算,它就是从向量
抽象地看成两个向量的夹角,就可以得到一种新的运算,它就是从向量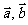 得到一个数量(即
得到一个数量(即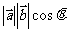 )的运算,这里
)的运算,这里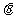 是向量
是向量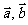 的夹角。
的夹角。
(2)进一步表述
引进“向量的数量积”等术语后,就可以把上面的结果进一步表述为:
已知两个向量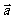 和
和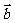 ,它们的夹角为
,它们的夹角为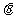 ,我们把数量
,我们把数量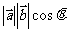 叫做
叫做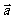 和
和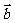 的数量积(或内积),记作
的数量积(或内积),记作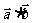 ,即
,即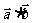 =
=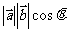 。
。
两个向量的夹角
问题 在上面的向量数量积的定义中,提到了“两个向量的夹角”的概念,它究竟代表什么意义呢?
从实际背景中的“力”和“位移”的夹角出发,展开讨论,得到下面的结论:
对于两个非零向量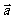 和
和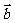 ,作
,作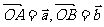 ,则
,则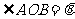 (
(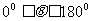 )叫做向量
)叫做向量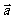 和
和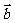 的夹角。
的夹角。
特别地,当向量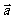 与
与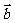 的夹角分别等于
的夹角分别等于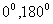 和
和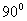 时,两个向量分别是同向、反向和垂直。向量
时,两个向量分别是同向、反向和垂直。向量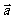 与
与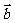 垂直,记作
垂直,记作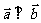 。
。
在讨论中应注意上述定义中对向量的“非零”限制。
平面向量的数量积
(3)表述的精确化
问题 在进一步弄清了“向量的夹角”的意义以后,应该怎样更精确地表述向量的数量积的概念?
问题 零向量有没有数量积?应该如何定义?
问题 在实际的“求功运算”中是怎样解决这个问题的?
通过讨论,得到“数量积”的定义:
已知两个向量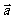 和
和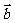 ,它们的夹角为
,它们的夹角为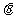 ,我们把数量
,我们把数量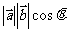 叫做
叫做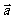 和
和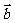 的数量积(或内积),记作
的数量积(或内积),记作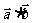 ,即
,即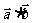 =
=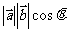 。同时规定:
。同时规定: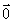 与任何向量的数量积为0,即
与任何向量的数量积为0,即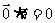 。
。
(4)对定义的理解
① 尽管向量数量积是从求功运算中抽象出来的,但是,它已经是一种抽象的数学运算了。一般地,它已经不具有“求功”的具体意义了。在引入向量的数量积以后,物理学中的功的概念就可以用数学语言表述为:功就是力与在其作用下物体产生的位移的数量积,即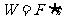
② 两个向量数量积的结果是一个实数,这与向量的加法、减法和数乘运算是不同的。
③ 注意: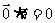 ,等式右边的零是一个实数,而不是零向量。
,等式右边的零是一个实数,而不是零向量。
数量积的运算性质
问题 向量的数量积有什么样的性质?
在实数乘法中,我们有: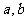 同号时,
同号时,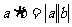 ,特别地
,特别地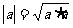 ,
,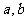 异号时,有
异号时,有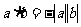 。在向量的数量积中,类似的结论成立吗?
。在向量的数量积中,类似的结论成立吗?
经过讨论得到下面的结论:
当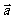 与
与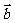 同向时,
同向时,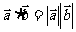 ,特别地,
,特别地,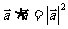 或
或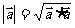 ;
;
当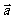 与
与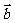 反向时,
反向时,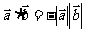 。
。
用类似的方法,可以得到下面的结论:
设向量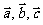 和实数
和实数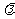 ,则向量的数量积满足下列运算律:
,则向量的数量积满足下列运算律:
①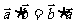 ;
;
②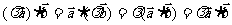 ;
;
③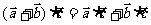
我们已经学习了向量的加法、减法和数乘,它们的运算结果都是向量,那么向量与向量之间有没有“乘法”运算呢?这种新的运算结果又是什么呢?
联想:物理中,功就是矢量与矢量“相乘”的结果。
问题 物理学中的“功”是通过什么方法计算出来的?
通过对物理公式
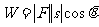
(其中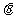 是F与
是F与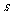 的夹角)的分析,得到如下结论:
的夹角)的分析,得到如下结论:
(1)功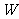 是两个向量
是两个向量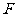 和
和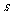 的某种运算的结果,而且这个结果是一个数量;
的某种运算的结果,而且这个结果是一个数量;
(2)功不仅与力和位移的大小有关,而且还与它们的方向有关,具体地,它和力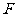 与位移
与位移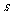 的夹角有关。
的夹角有关。
由此可见,“求功运算”作为一种新的向量运算,不同于我们以前学习过的其他数学运算。
21.(满分14分)
设 f (x) = px--2 ln x,且 f (e) = qe--2(e为自然对数的底数)
(I) 求 p 与 q 的关系;
(II) 若 f (x) 在其定义域内为单调函数,求 p 的取值范围;
(III) 设 g(x) = ,若在 [1,e] 上至少存在一点x0,使得 f (x0) > g(x0)
成立, 求实数 p 的取值范围.
湛江二中2010届高三第二次月考理科数学
20.(满分12分)
已知函数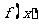 是定义在
是定义在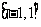 上的奇函数,在
上的奇函数,在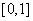 上
上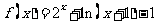

(Ⅰ)求函数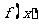 的解析式;并判断
的解析式;并判断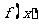 在
在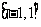 上的单调性(不要求证明)
上的单调性(不要求证明)
(Ⅱ)解不等式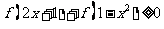 .
.



19.(满分14分)
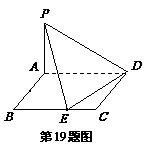 如图,四边形
如图,四边形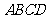 为矩形,且
为矩形,且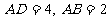 ,
,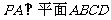 ,
,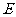 为
为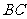 上的动点.
上的动点.
(1) 当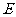 为
为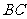 的中点时,求证:
的中点时,求证: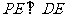 ;
;
(2) 设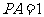 ,在线段
,在线段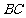 上存在这样的点E,使得二面角
上存在这样的点E,使得二面角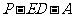 的大小为
的大小为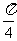 . 试确定点E的位置。
. 试确定点E的位置。


18.(满分14分)
某公司生产陶瓷,根据历年的情况可知,生产陶瓷每天的固定成本为14000元,每生产一件产品,成本增加210元.已知该产品的日销售量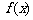 与产量
与产量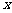 之间的关系式为
之间的关系式为
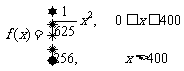 ,每件产品的售价
,每件产品的售价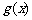 与产量
与产量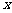 之间的关系式为
之间的关系式为
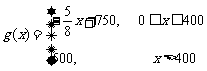 .
.
(Ⅰ)写出该陶瓷厂的日销售利润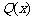 与产量
与产量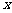 之间的关系式;
之间的关系式;
(Ⅱ)若要使得日销售利润最大,每天该生产多少件产品,并求出最大利润. 


17.(满分14分)
已知: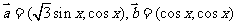 ,
,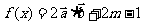 (
(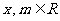 ).
).
(1) 求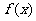 关于
关于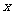 的表达式,并求
的表达式,并求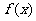 的最小正周期;
的最小正周期;
(2) 若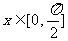 时
时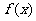 的最小值为5,求
的最小值为5,求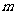 的值.
的值.

16.(满分12分)
已知非空集合 ,
,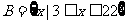 ,求使
,求使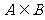 成立的
成立的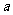 的取值。
的取值。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com