
12.已知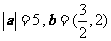 ,且
,且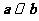 ,则
,则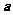 的坐标为
.
的坐标为
.
12答案: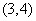 或
或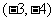
解析: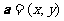 ,则
,则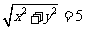 且
且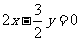 ,解得
,解得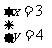 或
或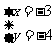 .
.
11.函数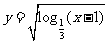 的定义域是 .
的定义域是 .
11答案: 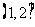
解析:由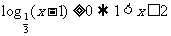 .
.
10.已知集合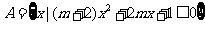 ,
,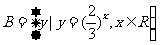 ,则使得
,则使得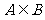 成立的所有实数
成立的所有实数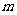 的取值范围是
的取值范围是
A.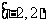 B.
B.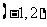 C.
C.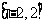 D.
D.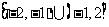
10答案:A
解析: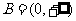 ,令
,令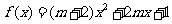 ,
,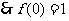 ,若
,若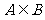 ,则有
,则有
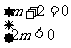 或
或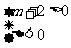 或
或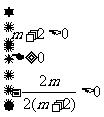 得,
得,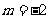 或
或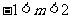 或
或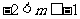
故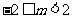 .
.
9.用砖砌墙,第一层(底层)用去了全部砖块的一半多一块,第二层用去了剩下的一半多一块,…,依次类推,每一层都用去了前一层剩下的一半多一块,如果到第9层恰好砖用光.
那么,共用去的砖块数为
A.1022 B.1024 C.1026 D.1028
9答案:A
解析:共用砖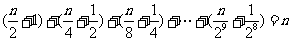 ,解得
,解得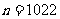
8.设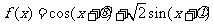 是偶函数,其中
是偶函数,其中 均为锐角,且
均为锐角,且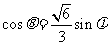 ,则
,则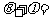
A.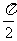 B.
B.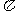 C.
C.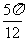 D.
D.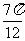
8答案:D
解析:将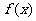 展开得,
展开得,
由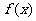 是偶函数,所以
是偶函数,所以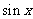 前的系数
前的系数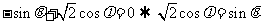 ,
,
联立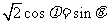 与
与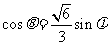 ,平方相加可得
,平方相加可得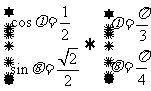 ,
,
故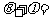
 .
.
7. 当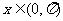 时,函数
时,函数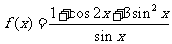 的最小值为
的最小值为
A.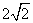 B.3
C.
B.3
C.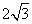 D.4
D.4
7答案:B
解析:由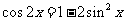 ,整理得
,整理得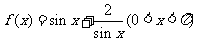 .
.
令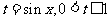 ,则函数
,则函数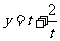 在
在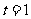 时有最小值3.
时有最小值3.
6.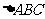 中,
中,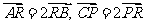 ,若
,若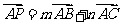 ,则
,则
A.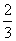 B.
B.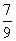 C.
C.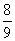 D.
D.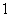
6答案:B
解析:由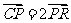 知,
知,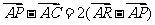 ,知
,知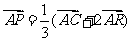
同时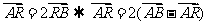 ,得
,得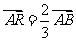
故有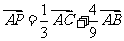 ,所以
,所以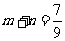 .
.
5.已知函数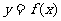 的图象与函数
的图象与函数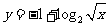 的图象关于直线
的图象关于直线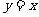 对称,则
对称,则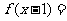
A.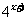 B.
B.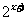 C.
C.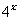 D.
D.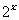
5答案:C
解析:由题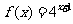 ,故
,故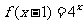 .
.
4.若等比数列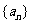 的公比为
的公比为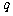 ,则“
,则“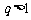 ”是“
”是“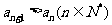 ”的
”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
4答案:D
解析:可以借助反例说明:①如数列: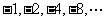 公比为
公比为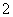 ,但不是增数列;
,但不是增数列;
②如数列: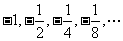 是增数列,但是公比为
是增数列,但是公比为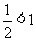 .
.
3.已知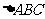 中,
中,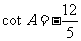 ,则
,则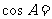
A.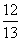 B.
B.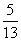 C.
C.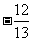 D.
D.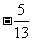
3答案:C
解析:由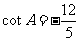 知
知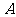 为钝角,再由
为钝角,再由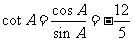 ,
,
求得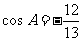 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com