
2. 函数单调性可以从三个方面理解
(1)图形刻画:对于给定区间上的函数f(x),函数图象如从左向右连续上升,则称函数在该区间上单调递增,函数图象如从左向右连续下降,则称函数在该区间上单调递减.
(2)定性刻画:对于给定区间上的函数f(x),如函数值随自变量的增大而增大,则称函数在该区间上单调递增,如函数值随自变量的增大而减小,则称函数在该区间上单调递减.
(3)定量刻画,即定义.
上述三方面是我们研究函数单调性的基本途径.
1. 增函数、减函数的定义
一般地,对于给定区间上的函数 ,如果对于属于这个区间的任意两个自变量的值
,如果对于属于这个区间的任意两个自变量的值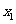 、
、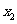 ,当
,当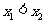 时,都有
时,都有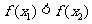 (或都有
(或都有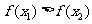 ),那么就说
),那么就说 在这个区间上是增函数(或减函数).
在这个区间上是增函数(或减函数).
如果函数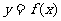 在某个区间上是增函数(或减函数),就说
在某个区间上是增函数(或减函数),就说 在这一区间上具有(严格的)单调性,这一区间叫做
在这一区间上具有(严格的)单调性,这一区间叫做 的单调区间.如函数是增函数则称区间为增区间,如函数为减函数则称区间为减区间.
的单调区间.如函数是增函数则称区间为增区间,如函数为减函数则称区间为减区间.
12.某市有小灵通与全球通两种手机,小灵通手机的月租费为25元,接听电话不收费,打出电话一次在3 min以内收费0.2元,超过3 min的部分为每分钟收费0.1元,不足1 min按1 min计算(以下同).全球通手机月租费为10元,接听与打出的费用都是每分钟0.2元.若某人打出与接听次数一样多,每次接听与打出的时间在1 min以内、1到2 min以内、2到3 min以内、3到4 min以内的次数之比为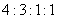 . 问:根据他的通话次数应该选择什么样的手机才能使费用最省?(注:m到m+1 min以内指含m min,而不含m+1
min)
. 问:根据他的通话次数应该选择什么样的手机才能使费用最省?(注:m到m+1 min以内指含m min,而不含m+1
min)
[解析]设小灵通每月的费用为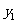 元,全球通的费用为
元,全球通的费用为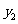 元,分别在1 min以内、2 min以内、3
min以内、4 min以内的通话次数为4x、3x、x、x,则
元,分别在1 min以内、2 min以内、3
min以内、4 min以内的通话次数为4x、3x、x、x,则
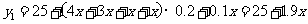 ,
,
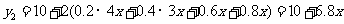 .
.
令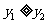 ,即
,即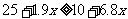 ,解得
,解得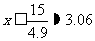 .
.
∴总次数为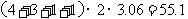 .
.
故当他每月的通话次数小于等于55次时,应选择全球通,大于55次时应选择小灵通.
第二节 函数的单调性
自主学习
11. ( 2006年重庆)已知定义域为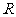 的函数
的函数 满足
满足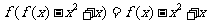 ,
,
(1)若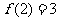 ,求f(1);又若
,求f(1);又若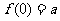 ,求
,求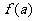 ;
;
(2)设有且仅有一个实数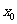 ,使得
,使得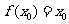 ,求函数
,求函数 的解析表达式.
的解析表达式.
[解析](1)因为对任意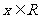 ,有
,有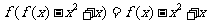 ,所以
,所以
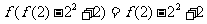 ,
,
又由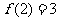 ,得
,得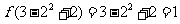 ,即
,即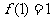 .
.
若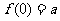 ,则
,则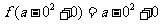 ,即
,即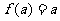 .
.
(2)因为对任意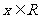 ,有
,有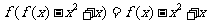 ,
,
又因为有且只有一个实数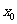 ,使得
,使得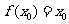 ,
,
所以对任意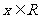 ,有
,有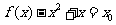
在上式中令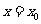 ,有
,有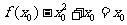
又因为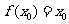 ,所以
,所以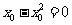 ,故
,故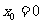 或
或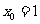 .
.
若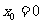 ,则
,则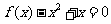 ,即
,即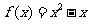 .
.
但方程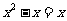 有两个不同实根,与题设条件矛质,故
有两个不同实根,与题设条件矛质,故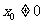 .
.
若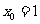 ,则有
,则有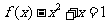 ,即
,即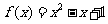 ,易验证该函数满足题设条件.
,易验证该函数满足题设条件.
综上,所求函数为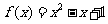
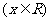 .
.
10.设函数f(x)=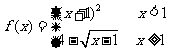 ,
,
则使得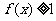 的x的取值范围是
的x的取值范围是 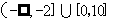 .
.
三 解答题
9.(2006年辽宁)设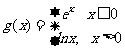 ,则
,则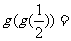
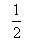 .
.
8.(2004浙江文)已知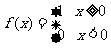 则不等式
则不等式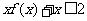 的解集是
的解集是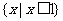 .
.
7.函数y=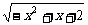 的定义域为
的定义域为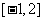 ,值域为
,值域为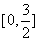 .
.
6.(2006年广东)函数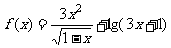 的定义域是 ( B
)
的定义域是 ( B
)
A.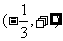 B.
B.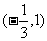 C.
C.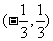 D.
D.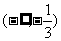
二 填空题
5.某种型号的手机自投放市场以来,经过两次降价,单价由原来的2000元降到1280元,则这种手机平均每次降价的百分率是 ( D )
A.10% B.15% C.18% D.20%
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com