
11.

10.

9. 

1.已知集合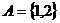 ,则满足
,则满足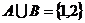 的集合
的集合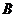 的个数共有( )个
的个数共有( )个
A.1
B. 2
C. 3
D. 4
2.函数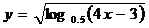 的定义域为 ( )
的定义域为 ( )
A.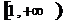 B.
B. 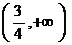
 C.
C. 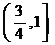 D.
D.
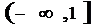

3.
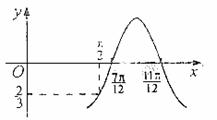
已知函数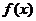 =Acos(
=Acos(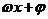 )的图象如图所示,
)的图象如图所示,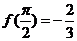 ,则
,则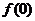 =( )
=( )
 A.
A.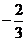 B.
B. 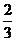



C.- 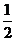 D.
D.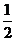

4.若将函数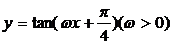 的图像向右平移
的图像向右平移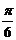 个单位长度后,与函数
个单位长度后,与函数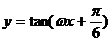 的图像重合,
的图像重合,
则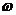 的最小值为( )
的最小值为( ) 
A. 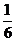 B.
B.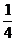 C.
C.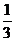 D.
D.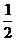



5.已知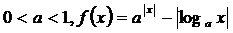 的实根个数是( )
的实根个数是( )
A.1个 B.2个 C.3个
D.1个或2个或3个
6.在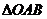 中,
中,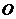 为坐标原点,
为坐标原点,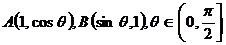 ,则当
,则当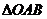 的面积达到最大值时,
的面积达到最大值时,
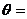 (
)
(
)
A.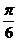 B.
B.
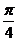 C.
C. 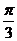 D.
D.
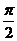

7. 设函数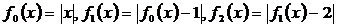 ,则函数
,则函数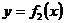 的图象与
的图象与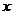 轴所围成的
轴所围成的
图形中的封闭部分的面积是( )
A. 4
B. 5
C. 6
D. 7
8.正实数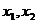 及函数
及函数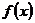 满足
满足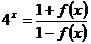 ,且
,且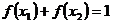 ,则
,则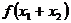 的最小值为( )
的最小值为( )
A.4
B. 2
C.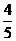 D.
D.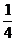

二、填空题(本大题共7小题,每小题5分,共35分)
9.已知命题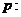
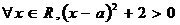 ,则
,则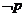 是
是

10.若不等式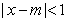 成立的充分不必要条件是
成立的充分不必要条件是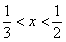 ,则实数
,则实数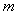 的取值范围是
的取值范围是 .
.

11.设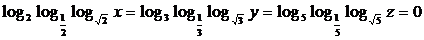 ,则
,则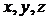 按从小到大的顺序
按从小到大的顺序
排列是

12.已知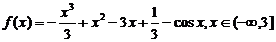 ,若
,若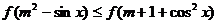 对
对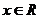 恒成立,
恒成立,
实数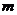 的取值范围是
的取值范围是

13.在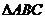 中,角A,B,C所对的边长分别为
中,角A,B,C所对的边长分别为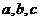 ,若
,若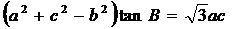 ,
,
则角B的值为

14.关于函数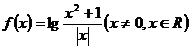 有下列命题:
有下列命题:
①函数y=f(x)的图象关于y轴对称。
②当x>0时,f(x)是增函数;当x<0时,f(x)是减函数。
③函数f(x)的最小值是lg2。
④当-1<x<0或x>1时,f(x)是增函数。
⑤f(x)无最大值,也无最小值。
其中正确的命题的序号是 。(注:把你认为正确的命题的序号都填上)
。(注:把你认为正确的命题的序号都填上)

15.在计算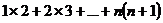 时,有如下一种算法:
时,有如下一种算法:
先将和式中第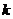 项变形为:
项变形为: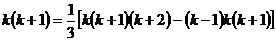 ,由此得
,由此得
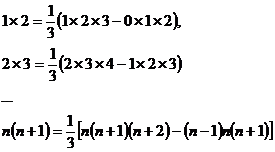

将以上各式相加,得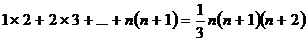 .
.
类比上述方法,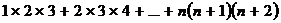 的化简结果是
的化简结果是

同升湖实验学校2010届高三第二次月考
数学试卷(理)
答题卷
21.解(1)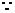
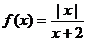 ,
,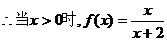
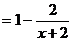
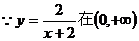 上是减函数
上是减函数
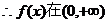 上是增函数.……………………4分
上是增函数.……………………4分
(2)原方程即: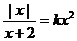
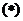
①
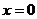 恒为方程
恒为方程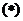 的一个解.……………………5分
的一个解.……………………5分
②当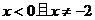 时方程
时方程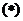 有解,则
有解,则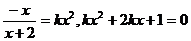
当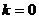 时,方程
时,方程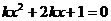 无解;
无解;
当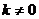 时,
时,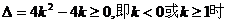 ,方程
,方程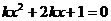 有解.
有解.
设方程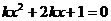 的两个根分别是
的两个根分别是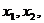 则
则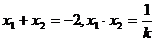 .
.
当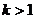 时,方程
时,方程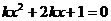 有两个不等的负根;
有两个不等的负根;
当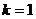 时,方程
时,方程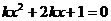 有两个相等的负根;
有两个相等的负根;
当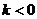 时,方程
时,方程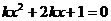 有一个负根………………………8分
有一个负根………………………8分
③当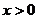 时,方程
时,方程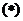 有解,则
有解,则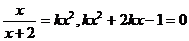
当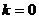 时,方程
时,方程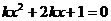 无解;
无解;
当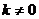 时,
时,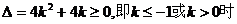 ,方程
,方程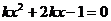 有解.
有解.
设方程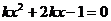 的两个根分别是
的两个根分别是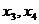
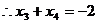 ,
,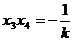
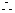 当
当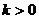 时,方程
时,方程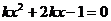 有一个正根,
有一个正根,
当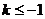 时,方程
时,方程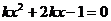 没有正根.……………………11分.
没有正根.……………………11分.
综上可得,当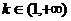 时,方程
时,方程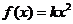 有四个不同的实数解.……13分.
有四个不同的实数解.……13分.
20.解:(1)由题意知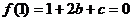 ,∴
,∴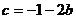
记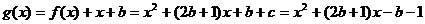
 则
则 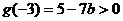
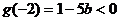
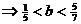
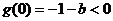
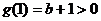
即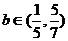 …………………..7分
…………………..7分
(2)令u=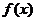 。∵
。∵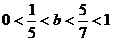 ∴
∴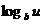 在(0,+∞)是减函数
在(0,+∞)是减函数
而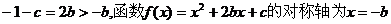
∴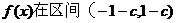 上为增函数,
上为增函数,
从而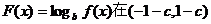 上为减函数
上为减函数
且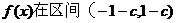 上恒有
上恒有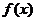 >0 ,只需
>0 ,只需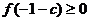 ,
,
且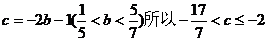 ………………….13分
………………….13分
19. 解:(1)由已知条件可知:降低征税率为(10-x)﹪,农产品收购量为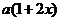 ﹪,农贸公司收购农产品总额为200
﹪,农贸公司收购农产品总额为200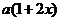 ﹪………6分
﹪………6分
∴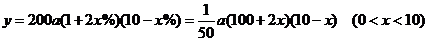 ………6分
………6分
(2)由题意知: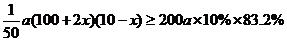 ………8分
………8分
即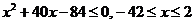
∵0<x<10,∴0<x≤2………12分
答:略 ………13分
………13分
18.解:(1)解:设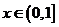 ,则
,则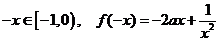
∵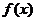 是奇函数,∴
是奇函数,∴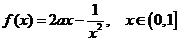 ………6分
………6分
(2)证明: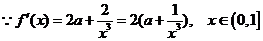
∴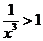 又知a>-1,∴
又知a>-1,∴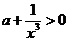
即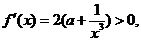 ∴
∴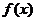 在
在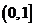 上单调递增………12分
上单调递增………12分
17.
|
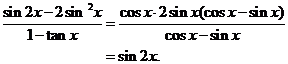
|
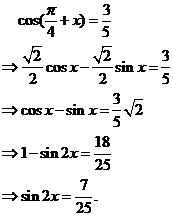
|
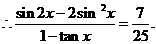
16.解: (Ⅰ)因为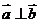 ,所以
,所以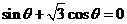 得
得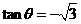 又
又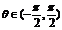 ,所以
,所以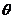 =
=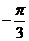
(Ⅱ)因为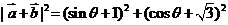 =
=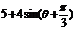
所以当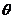 =
=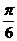 时,
时, 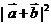 的最大值为5+4=9 故
的最大值为5+4=9 故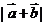 的最大值为3
的最大值为3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com