
13. 10 ,16 ;15. (0°,60°) ;
24.(本小题满分10分)选修4-5:不等式选讲
已知函数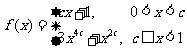 满足
满足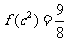 ;
;
(1)求常数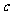 的值;
的值;
(2)解不等式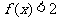 .
.
海南省洋浦中学2010届高三年级第9次月考测试答案
第Ⅱ卷(非选择题) (共90分)
23.(本小题满分10分)选修4-4:坐标系与参数方程
已知直线L过点P(-3,-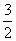 )与圆C:
)与圆C: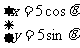 (
(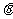 为参数)
为参数)
相交于A、B两点。
(1) 若∣AB∣=8,求直线L的方程;
(2)求弦AB的中点M的轨迹方程。
22.(本小题满分10分)选修4-1:几何证明选讲
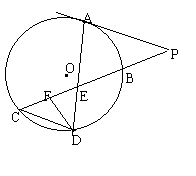
如图所示,已知PA与⊙O相切,A为切点,PBC为割线,
弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF·EC.
(1)求证:ÐP=ÐEDF;
(2)求证:CE·EB=EF·EP.
21. 如图,设F是椭圆
如图,设F是椭圆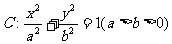 的左焦点,直线l为其左准线,直线l与x轴交于点P,线段MN为椭圆的长轴,已知
的左焦点,直线l为其左准线,直线l与x轴交于点P,线段MN为椭圆的长轴,已知
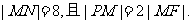
(1)求椭圆C的标准方程;
(2)若过点P的直线与椭圆相交于不同两点A、B求证:∠AFM=∠BFN;
(3)求三角形ABF面积的最大值。
 请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目对应的题号涂黑。
请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目对应的题号涂黑。
20.已知函数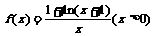 .
.
(1)试判断函数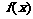 在
在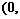
 上单调性并证明你的结论;
上单调性并证明你的结论;
(2)若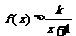 恒成立,求整数
恒成立,求整数 的最大值;
的最大值;
(3)求证: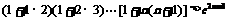 。
。
19.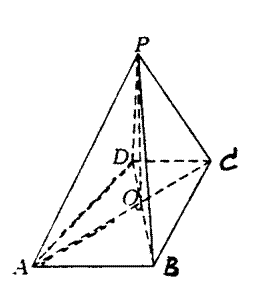 如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB//CD,AC⊥DB,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=
如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB//CD,AC⊥DB,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=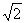 ,PB⊥PD.
,PB⊥PD.
(Ⅰ)求异面直线PD与BC所成角的余弦值;
(Ⅱ)求二面角P-AB-C的大小;
(Ⅲ)设点M在棱PC上,且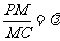 ,问
,问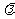 为何值时,PC⊥平面BMD.
为何值时,PC⊥平面BMD.
18.某果园要将一批水果用汽车从所在城市甲运至销售商所在城市乙,已知从城市甲到城市乙只有两条公路,且运费由果园承担.如果果园恰能在约定日期(×月×日)将水果送到,则销售商一次性支付给果园20万元,若在约定日期前送到,每提前一天销售商将多支付给果园1万元;若在约定日期后送到,每迟到一天,销售商将少支付给果园1万元.为保证水果新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中一条公路运送水果,已知下表内的信息
|
统计信息 汽车行驶路线 |
不堵车的情况下到达 城市乙所需时间(天) |
堵车的情况下到达 城市乙所需时间(天) |
堵车的 概率 |
运费 (万元) |
|
公路1 |
2 |
3 |
|
1.6 |
|
公路2 |
1 |
4 |
|
0.8 |
(1)记汽车走公路1是果园获得的毛利润为ξ(万元),求ξ的分布列和数学期望Eξ; (2)假设你是果园的决策者,你选择哪条公路运送水果有可能让果园获得的毛利润更多? (注:毛利润=销售商支付给果园的费用-运费).
17.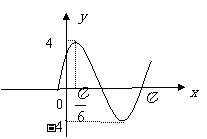 已知
已知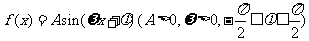 的图象如图
的图象如图
(Ⅰ)求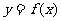 的解析式;
的解析式;
(Ⅱ)说明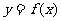 的图象是由
的图象是由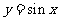 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
15. ;16.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com