
3.交流思想与体会。主要谈谈对微积分发明的感想及其对自己的启示。
(1)微积分的发明不是一蹴而就的,而是人类集体智慧的结晶,是无数科学家长期奋斗的结果。
(2)数学来源于实践,没有当时大量实际问题的涌现,没有科学家深入实际,将大量实际问题转化为数学问题的研究,是不可能产生微积分理论的。
(3)渊博的知识,谦虚的治学作风,是学术上取得成就的必要条件。牛顿说“如果我看得更远些,那是因为我站在巨人的肩膀上”,牛顿与莱布尼茨的高明之处之一就是善于总结他人的研究成果。提出自己的主张。
……
布置作业
恩格斯说:“在一切理论在就中,未必再有什么像17世纪下半叶微积分的发现那样被看作人类精神的最高胜利了。如果在某个地方我们看到人类精神的纯粹和唯一的功绩,那就正是在这里。”请你结合今天上课的内容,谈谈你对恩格斯这段话的理解。
2.介绍刘徽、笛卡尔、费马、牛顿与菜布尼茨的数学方法。
(1)刘徽的“割圆术”。
魏晋南北朝时期的数学家刘徽提出割圆术作为计算圆的周长、面积以及圆周率的基础。其方法是“割之弥细,所失弥少,割之又割,以至于不可割,则与圆台体而无所失矣。”也就是说:刘徽用圆内接正多边形去逐步逼近圆。
如图,设圆面积为S,半径为r,圆内接正n边形边长为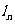 ,周长为
,周长为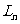 ,面积为
,面积为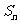 。将边数加倍后,得到圆内接正2n边形,其边长、周长、面积分别记为
。将边数加倍后,得到圆内接正2n边形,其边长、周长、面积分别记为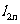 、
、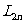 、
、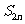 ,则
,则
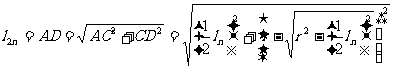 ,
,
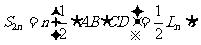 ,
,
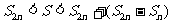 。
。
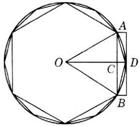
当n无限增大时,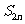 便趋于圆的面积,祖冲之按刘徽割圆术从正六边形连续算到正24576边形时,得到圆周率π的上下限:3.1415926<π<3.1415927。这是当时世界在这一领域的最高水平。
便趋于圆的面积,祖冲之按刘徽割圆术从正六边形连续算到正24576边形时,得到圆周率π的上下限:3.1415926<π<3.1415927。这是当时世界在这一领域的最高水平。
刘徽割圆的逼近思想是以后极限思想的萌芽,为定积分概念的形成积累了素材。
(2)笛卡儿求切线的“圆法”。
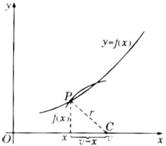
法国数学家笛卡儿用代数方法(即圆法)求出了曲线在其上某一点处的切线方程。
笛卡儿求曲线y=f(x)过点P(x,f(x))的切线斜率的“圆法”是:(如图)过C点(曲线在点P处的法线与x轴的交点)作半径为r=CP的圆C: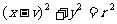 。因CP是曲线y=f(x)在P点的法线,则P应是曲线与圆C的“重交点”。若
。因CP是曲线y=f(x)在P点的法线,则P应是曲线与圆C的“重交点”。若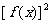 是多项式函数,有重交点就相当于方程
是多项式函数,有重交点就相当于方程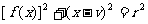 有重根x=e,从而
有重根x=e,从而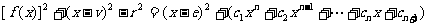 ,比较系数得v与e的关系,代入e=x,便得过P点的切线斜率
,比较系数得v与e的关系,代入e=x,便得过P点的切线斜率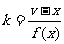 。
。
以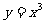 为例。点
为例。点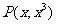 。设
。设
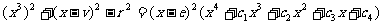 ,经特定系数法得知:
,经特定系数法得知:
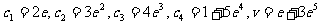 。
。
故切线斜率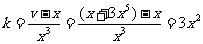 。
。
笛卡尔的代数方法正是后来求切线方法的雏形,牛顿就是以笛卡儿圆法为起跑点而踏上研究微积分道路的。
(3)费马求极值的代数方法。
法国数学家费马求函数y=f(x)在点a处极值(如果存在的话)的代数方法是:用a+e代替a,并使f(a+e)与f(a)“逼近”,即f(a+e)→f(a)。
消去公共项后,用e除两边,再令e消失,即
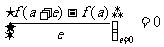 ,
,
由此方程求出的a就是f(x)的极值点。
以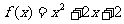 为例,
为例,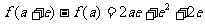 ,
,
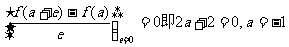 。
。
-1是f(x)的极值点。
费马的方法几乎相当于后来微分学中的方法,只是以符号e代替了增量△x。可以说费马已经走到了微积分的边缘了,再往前迈一步,微积分的发明人也许要改弦易辙了。
(4)牛顿的“流数术”
牛顿以他的运动学为背景,总结了笛卡尔、费马等人的方法,提出了具有一般意义的“流数”概念,他的《流数简论》的问世标志着微积分的诞生。
以函数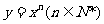 为例说明流数概念。
为例说明流数概念。
设x变为x+o,则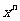 变为
变为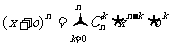 ,
,
 ,设增量o消失,它们的比就是
,设增量o消失,它们的比就是
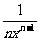 ,这就是x的流数与
,这就是x的流数与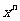 的流数之比。
的流数之比。
流数就是现在的微商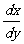 。
。
然后牛顿使用流数概念应用于求曲线切线、曲率、拐点,曲线求长、求积、求引力与引力中心等大量问题,展示了流数及其算法的极大普通性与系统性。
同时莱布尼茨从几何角度关于特征三角形的研究也得到了与牛顿类似的结论与算法。
2.前面我们学习了极限与导数,已经领咯到了在利用导数求曲线的切线方程、讨论函数的单调性与极值问题中所显示出的无比优越性。我们不禁会问;牛顿与菜布尼茨是怎样发明这样高明的数学方法的,是灵感在一夜之间的闪现还是前人长期努力的结晶?
1.用电脑展示微积分发明者--牛顿与莱布尼茨的像片。


微积分发明人
20、(1)

 …………2分
…………2分

令 得
得
 得
得
 的单调递增区间为
的单调递增区间为 ;单调递减区间为
;单调递减区间为 …………4分
…………4分
(2): 在区间
在区间 为增函数,
为增函数,
 在
在 上恒成立…………6分
上恒成立…………6分
 在
在 上恒成立
上恒成立
 ………………9分
………………9分
又 时,
时, 不为常函数
不为常函数
 所求m的取值范围为
所求m的取值范围为  ……………10分
……………10分
(3)令 ………11分
………11分
令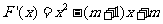 得
得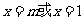 …………12分
…………12分
|
x |
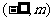 |
m |
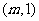 |
1 |
 |
|
F’(x) |
+ |
0 |
- |
0 |
+ |
|
F(x) |
↗ |
极大值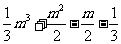 |
↘ |
极小值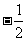 |
↗ |
由题得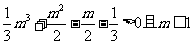 ……………16分
……………16分
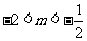 ……………18分
……………18分
19、(1)
……6分
(2) ……………8分
……………8分
令 ,得
,得 …………10分
…………10分
列表得当 ,
, ………15分
………15分
答:当 时,最大绿化面积为
时,最大绿化面积为 …………16分
…………16分
18、假设该函数图象上存在两点 的连线平行x轴,
的连线平行x轴,
…………4分
则
即 …………6分
…………6分
 即
即
 与
与 矛盾
…………10分
矛盾
…………10分
假设错误,即函数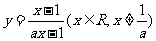 任意两点的连线不平行x轴……12分
任意两点的连线不平行x轴……12分
17、(1)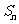 是
是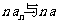 的等差中项,
的等差中项,
当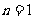 时,
时,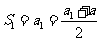
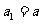 ……………2分
……………2分
当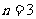 时,
时,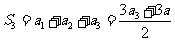
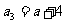 ………4分
………4分
(2)猜想: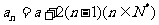 ………………6分
………………6分
证明:①当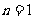 时,由(1)可知等式成立;……………7分
时,由(1)可知等式成立;……………7分
②假设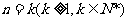 时等式成立,即:
时等式成立,即: ……8分
……8分
则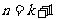 时,
时,
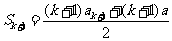
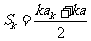
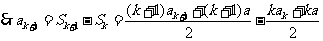
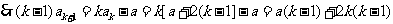
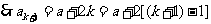
即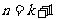 时等式也成立
……………14分
时等式也成立
……………14分
综合①②知: 对任意
对任意 均成立 ………16分
均成立 ………16分
16、设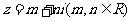
由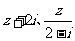 均为实数得
均为实数得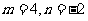 ,……………8分
,……………8分
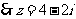
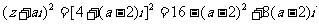 ………10分
………10分
由题得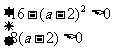
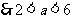 ……………14分
……………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com