
自学教材例3,完成下列练习(约10分钟)
(教师注意:理解例3,事实上是对我们这一节课的所有内容的一个诠释,老师们需要注意的是,有些老师往往认为这一部分内容很简单,而忽视教学,事实上,这一部分内容是很关键的,是为我们以后数形结合思想的渗透打基础的,所以不能忽视.而事实上,很多学生确实不会.因为函数的概念比较抽象,学生们刚刚学习完函数,对于函数的表示法,也是有所畏惧的,身为老师,我们应该更多的去引导.)
(自学引导:透彻的理解例3,练习一<2>要能熟练的得出结论,注意培养自己作图的基本功)
练习一:<1>例3是用三种方法来表示函数的,请你说一下这三种表示方法的各自的特点;
<2>完成教材第23页练习1、3;
自学教材例4,完成下列练习(约10分钟)
(教师注意::注意练习二的第<1>题,事实上告诉了我们三种表示方法在具体问题中所体现的不同地位,第<2>题是一个初中的知识,同学们需要画出图像来得到答案,也需要总结出一些结论,譬如关于二次函数,我们不画图像,仅仅凭借解析式的对称轴和定义域,能否得到值域?这是需要我们探究的.第<3>题是一个实际生活问题,我们所要学习的知识都是要运用于实际生活的,这样的问题,我们的学生能解答出来吗?所以第<3>题实际上是培养学生的具体问题具体分析、学以致用的能力的)
(自学引导:具体问题具体分析,注意培养自己的思维发散能力)
[教学效果]:关键是培养学生的作图能力.
练习二:<1>根据例4,你能得出一些什么感想?实际生活中你能想象得到运用我们所学的数学知识得到一些结论吗?
(学以致用,是我们学习的根本,只有让学生们认识到,我们的学习在实际生活中是有用的,才能激发学生学习的兴趣,才能把我们的教学推进下去,事实上,这也是我们教育的目标.培养有用的人才,是我们老师的责任.说到这一点,例4的讲解应该是很有必要的了.)
<2>函数y=2x2+4x-6,x∈[3,5)的值域是________
(引申:如果我们不画出函数的图像,你能求出这个二次函数的值域吗?)
[教学效果]:渗透学生数形结合的思想,发挥学生的主观能动性.
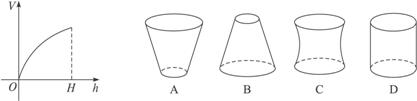
<3>向高为H的水瓶中注水,注满为止,如果注水量V与水深h的函数关系的图象如图所示,那么水瓶的形状是( )
结论:<1>、<2>略;<3>观察图象,根据图象的特点发现:取水深h=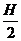 ,注水量V′>
,注水量V′>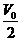 ,即水深为一半时,实际注水量大于水瓶总水量的一半;A中V′<
,即水深为一半时,实际注水量大于水瓶总水量的一半;A中V′<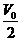 ,C、D中V′=
,C、D中V′=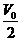 ,故排除A、C、D;
,故排除A、C、D;
(此题(练习二<3>)考查学生思维发散能力,可以当堂讲,可以留作思考)
[教学效果]:本节内容放到自习课上讲,培养学生发散思维的能力,数形结合的能力.
思考:已知2f(x)+f(-x)=3x+2,则f(x)=________.
[教学效果]:学生思考研究,根据反馈才能得到具体的信息.
2、注意训练学生的作图基本功,落实学生作图的基本功练习.
[教学效果]:教学目标和自学引导的出示其实已经把这节课的内容基本上点出来了,学生们基本上已经了解了函数的三种表示方法.
(自学引导:其实我们初中学习一次函数、二次函数、反比例函数的时候,我们已经接触到了函数的三种表示方法,譬如:用列表、描点、连线的方法画出函数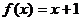 的图像,其中的列表,就可以类似的理解为列表法表示函数(当然,有序实数对比较多,我们只是找一些能表示函数基本规律的有序实数对列举出来),我们所画出的图像就是图像法表示函数,
的图像,其中的列表,就可以类似的理解为列表法表示函数(当然,有序实数对比较多,我们只是找一些能表示函数基本规律的有序实数对列举出来),我们所画出的图像就是图像法表示函数,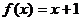 ,就是解析法来表示函数)
,就是解析法来表示函数)
(教师准备:教师应该事先把板书设计好)
1、理解函数的三种表示方法的区别与联系;会熟练的运用函数的三种表示方法来表示函数;
(五)归纳小结,布置作业。
从知识和方法两个方面让学生谈本节课的收获,并进行反思。
作业:层次一:教材第52页习题2-1A 6、7、8题 层次二:教材第53页习题2-1B2、3、4题
层次三:补充题:判断按下列函数的奇偶性:
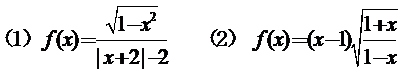
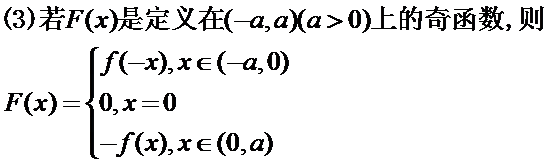
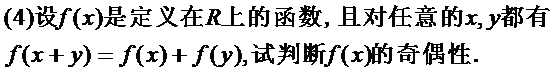
通过分层作业使学生进一步巩固本节课所学内容,并为学有余力和学习兴趣浓厚的学生提供进一步学习的机会
以上是对本节课的一些思考,不妥之处,敬请各位专家评委批评指正。
(四)、知识应用,巩固提高。
例1. 判断下列函数的奇偶性
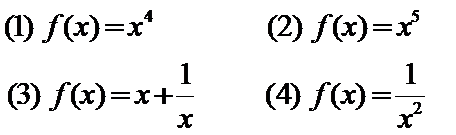
选例1的第(1)小题板书来示范解题步骤,其他例题让几个学生板演,其余学生在下面完成。
例1设计意图是归纳出判断奇偶性的步骤:
(1) 先求定义域,看是否关于原点对称;
(2) 再判断f(-x)=-f(x) 还是 f(-x)=f(x).
结合例1的答案,发动学生思考:一个函数奇偶性的可能情况有几种类型?(多媒体显示)
例1完成后,要求学生做练习,及时巩固,教师做好巡视指导
练习: 教材第53页,练习A第1题
下面来学习例2、例3
例2已知函数y=f(x)是偶函数,它在y轴右边的图象如下图,画出在y轴左边的图象. (多媒体显示)
例3
研究函数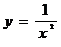 的性质并作出它的图像
的性质并作出它的图像
课件演示例2,板书例3.
例2 例3主要让学生体会学习了函数的单调性后为研究函数的性质带来的方便。根据奇、偶函数图像的对称性,只研究函数在y轴一侧的图像和性质就可以知道在另一侧的图像和性质。
(三) 学生探索、深化概念:
设计以下问题组织学生讨论思考回答
问题1:奇函数、偶函数的定义中有“任意”二字,说明函数的奇偶性是怎样的一个性质?与单调性有何区别?
问题2:-x与x在几何有何关系?具有奇偶性的函数的定义域有何特征?
问题3:如果一个函数是奇函数,且0在定义域内,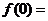 ?如果一个函数既是奇函数,又是偶函数,则
?如果一个函数既是奇函数,又是偶函数,则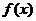 有何特性?
有何特性?
通过对三个问题的探讨,引导学生认识以下几点:(多媒体显示)
问题4:结合函数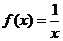 的图像回答以下问题:
的图像回答以下问题:
(1)对于任意一个奇函数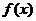 ,图像上的点P(x,
,图像上的点P(x, 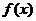 )关于原点的对称点P’的坐标是什么?点P’是否也在函数
)关于原点的对称点P’的坐标是什么?点P’是否也在函数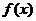 的图像上?由此可得到怎样的结论?
的图像上?由此可得到怎样的结论?
(2)如果一个函数的图像是以坐标原点为对称中心的中心对称图形,能否判断它的奇偶性?
学生通过交流探索问题4可以把奇函数的性质总结出来,然后教师发动学生自己研究一下偶函数图像的性质(教师板书)
(二)指导观察、形成概念。
数学中对称的形式也很多,这节课我们就同学们谈到的与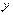 轴对称的函数展开研究。
轴对称的函数展开研究。
先思考一个问题:哪些函数的图象关于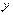 轴对称?试举例。
轴对称?试举例。
然后以函数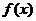 =x2和
=x2和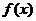 =︱x︱为例,学生动手作出图像,让学生回想,初中时怎样判断图象关于
=︱x︱为例,学生动手作出图像,让学生回想,初中时怎样判断图象关于
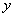 轴对称呢? 此时提出研究方向: 今天我们将从数值角度研究图象的这种特征,体现在自变量与函数值之间有何规律?
轴对称呢? 此时提出研究方向: 今天我们将从数值角度研究图象的这种特征,体现在自变量与函数值之间有何规律?
引导学生先把它们具体化,再用数学符号表示.借助课件演示(令 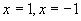 比较
比较
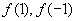 得出等式
得出等式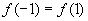 , 再令
, 再令 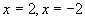 ,得到
,得到 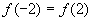 ) 让学生发现两个函数的对称性反应到函数值上具有的特性:
) 让学生发现两个函数的对称性反应到函数值上具有的特性: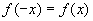 ,然后通过解析式给出严格证明,进一步说明这个特性对定义域内任意一个
,然后通过解析式给出严格证明,进一步说明这个特性对定义域内任意一个 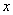 都成立.最后让学生用完整的语言给出偶函数定义,不准确的地方教师予以提示或调整.
都成立.最后让学生用完整的语言给出偶函数定义,不准确的地方教师予以提示或调整.
(1) 偶函数的定义:(板书)
设函数y=f(x)的定义域为D,如果对D内的任意一个x,都有-x∈D 且
f(-x)=f(x),那么f(x)就叫做偶函数.
接着提出新问题:
函数图象关于原点对称,它的自变量与函数值之间的数值规律是什么呢?然后多媒体展示两个学生非常熟悉的函数 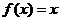 和
和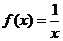 的图象让学生观察研究。
的图象让学生观察研究。
引导学生用类比的方法,得出结论,再鼓励学生给出奇函数的定义.
(2) 奇函数的定义(板书)
设函数y=f(x)的定义域为D,如果对D内的任意一个x,都有-x∈D 且
f(-x)= - f(x) ,那么f(x)就叫做奇函数.
(一)设疑导入、观图激趣。
1、用多媒体展示一组图片,让学生感受生活中的美:对称美,再让学生举例。
通过让学生观察图片导入新课,既激发了学生浓厚的学习兴趣,又为新知作好铺垫。
(五)归纳小结,布置作业。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com