
060]解:(1)根据题意,得
 ,解得
,解得
 抛物线的解析式为
抛物线的解析式为 ,顶点坐标是(2,4)
,顶点坐标是(2,4)
(2) ,设直线
,设直线 的解析式为
的解析式为
 直线经过点
直线经过点 点
点



(3)存在. ,
, ,
, ,
,
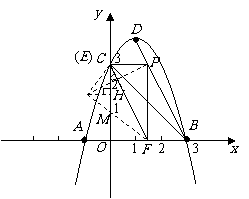
058]解:(1)令 ,得
,得 解得
解得 ,令
,令 ,得
,得
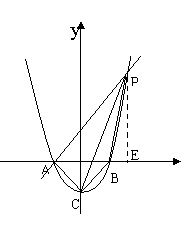 ∴ A
∴ A B
B C
C ··········· 3分
··········· 3分
(2)∵OA=OB=OC= ∴
∴ BAC=
BAC= ACO=
ACO= BCO=
BCO=
∵AP∥CB,∴ PAB=
PAB= ,过点P作PE
,过点P作PE
 轴于E,
轴于E,
则 APE为等腰直角三角形
APE为等腰直角三角形
令OE= ,则PE=
,则PE= ∴P
∴P
∵点P在抛物线 上 ∴
上 ∴
解得 ,
, (不合题意,舍去) ∴PE=
(不合题意,舍去) ∴PE= ················································· 4分
················································· 4分
∴四边形ACBP的面积 =
= AB•OC+
AB•OC+ AB•PE=
AB•PE= ························ 5分
························ 5分
(3). 假设存在∵ PAB=
PAB= BAC =
BAC = ∴PA
∴PA AC
AC
∵MG
 轴于点G, ∴
轴于点G, ∴ MGA=
MGA= PAC =
PAC =
在Rt△AOC中,OA=OC= ∴AC=
∴AC= ,在Rt△PAE中,AE=PE=
,在Rt△PAE中,AE=PE= ∴AP=
∴AP=  ·· 6分
·· 6分
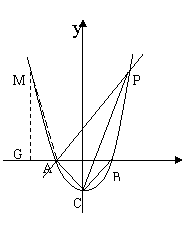 设M点的横坐标为
设M点的横坐标为 ,则M
,则M 
①点M在 轴左侧时,则
轴左侧时,则
(ⅰ) 当 AMG
AMG 
 PCA时,有
PCA时,有 =
= ∵AG=
∵AG= ,
,
MG= 即
即 解得
解得 (舍去)
(舍去)
 (舍去)………7分
(舍去)………7分
(ⅱ) 当 MAG
MAG 
 PCA时有
PCA时有 =
=
 即
即  ,解得:
,解得: (舍去)
(舍去)
 ∴M
∴M ·································································································· 8分
·································································································· 8分
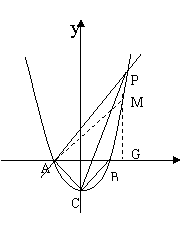
② 点M在 轴右侧时,则
轴右侧时,则
(ⅰ) 当 AMG
AMG 
 PCA时有
PCA时有 =
=
∵AG= ,MG=
,MG=
∴  解得
解得 (舍去)
(舍去)  ∴M
∴M
(ⅱ) 当 MAG
MAG
 PCA时有
PCA时有 =
= 即
即 
解得: (舍去)
(舍去)  ∴M
∴M ∴存在点M,使以A、M、G三点为顶点的三角形与
∴存在点M,使以A、M、G三点为顶点的三角形与 PCA相似,M点的坐标为
PCA相似,M点的坐标为 ,
, ,
,
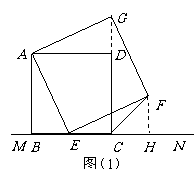 [059]解:(1)∵四边形ABCD和四边形AEFG是正方形
[059]解:(1)∵四边形ABCD和四边形AEFG是正方形
∴AB=AD,AE=AG,∠BAD=∠EAG=90º
∴∠BAE+∠EAD=∠DAG+∠EAD
∴∠BAE=∠DAG
∴△ BAE≌△DAG …………4分
(2)∠FCN=45º …………5分
理由是:作FH⊥MN于H
∵∠AEF=∠ABE=90º
∴∠BAE +∠AEB=90º,∠FEH+∠AEB=90º
∴∠FEH=∠BAE 又∵AE=EF,∠EHF=∠EBA=90º
∴△EFH≌△ABE …………7分
∴FH=BE,EH=AB=BC,∴CH=BE=FH
∵∠FHC=90º,∴∠FCH=45º …………8分
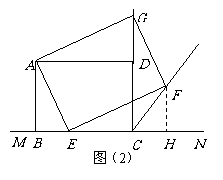 (3)当点E由B向C运动时,∠FCN的大小总保持不变,…………9分
(3)当点E由B向C运动时,∠FCN的大小总保持不变,…………9分
理由是:作FH⊥MN于H
由已知可得∠EAG=∠BAD=∠AEF=90º
结合(1)(2)得∠FEH=∠BAE=∠DAG
又∵G在射线CD上,∠GDA=∠EHF=∠EBA=90º
∴△EFH≌△GAD,△EFH∽△ABE ……11分
∴EH=AD=BC=b,∴CH=BE,∴==
∴在Rt△FEH中,tan∠FCN===
 ∴当点E由B向C运动时,∠FCN的大小总保持不变,tan∠FCN=
∴当点E由B向C运动时,∠FCN的大小总保持不变,tan∠FCN=
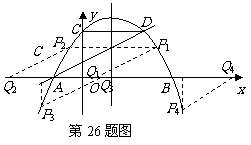
056]解:(1) C(3,0);
(2)①抛物线 ,令
,令 =0,则
=0,则 =
= , ∴A点坐标(0,c).
, ∴A点坐标(0,c).
∵ ,∴
,∴  ,∴点P的坐标为(
,∴点P的坐标为( ).
).
∵PD⊥ 轴于D,∴点D的坐标为(
轴于D,∴点D的坐标为( ). ……………………………………5分
). ……………………………………5分
根据题意,得a=a′,c= c′,∴抛物线F′的解析式为 .
.
又∵抛物线F′经过点D( ),∴
),∴ .……………6分
.……………6分
∴ .又∵
.又∵ ,∴
,∴ .∴b:b′=
.∴b:b′= .
.
②由①得,抛物线F′为 .
.
令y=0,则 . ∴
. ∴ .
.
∵点D的横坐标为 ∴点C的坐标为(
∴点C的坐标为( ).
).
设直线OP的解析式为 .∵点P的坐标为(
.∵点P的坐标为( ),
),
∴ ,∴
,∴ ,∴
,∴ .
.
∵点B是抛物线F与直线OP的交点,∴ .∴
.∴ .
.
∵点P的横坐标为 ,∴点B的横坐标为
,∴点B的横坐标为 .
.
把 代入
代入 ,得
,得 .
.
∴点B的坐标为 .∴BC∥OA,AB∥OC.(或BC∥OA,BC =OA),
.∴BC∥OA,AB∥OC.(或BC∥OA,BC =OA),
∴四边形OABC是平行四边形.
又∵∠AOC=90°,∴四边形OABC是矩形.
 [057](1)
[057](1) 
(2)∵ ,
, ,∴
,∴
当点 在
在 上运动时,
上运动时, ,
,
 ;
;
当点 在
在 上运动时,作
上运动时,作 于点
于点 ,
,
有 ∵
∵ ,∴
,∴
∴
(3)当 时,
时, ,
, ,
,
此时,过 各顶点作对边的平行线,与坐标轴无第二个交点,所以点
各顶点作对边的平行线,与坐标轴无第二个交点,所以点 不存在;
不存在;
当 时,
时, ,
, ,此时,
,此时, 、
、
055](1)过点 作
作 轴,垂足为
轴,垂足为 ,
,

 ;
;
又 ,
,
 ,
,
 点
点 的坐标为
的坐标为 ;············································ 4分
;············································ 4分
(2)抛物线 经过点
经过点 ,则得到
,则得到 ,························ 5分
,························ 5分
解得 ,所以抛物线的解析式为
,所以抛物线的解析式为 ;············································· 7分
;············································· 7分
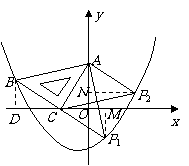
(3)假设存在点 ,使得
,使得 仍然是以
仍然是以 为直角边的等腰直角三角形:
为直角边的等腰直角三角形:
 若以点
若以点 为直角顶点;
为直角顶点;
则延长 至点
至点 ,使得
,使得 ,得到等腰直角三角形
,得到等腰直角三角形 ,··························· 8分
,··························· 8分
过点 作
作 轴,
轴, ;
;

 ,可求得点
,可求得点 ;········· 11分
;········· 11分
 若以点
若以点 为直角顶点;
为直角顶点;
则过点 作
作 ,且使得
,且使得 ,得到等腰直角三角形
,得到等腰直角三角形 ,·············· 12分
,·············· 12分
过点 作
作 轴,同理可证
轴,同理可证 ;··············································· 13分
;··············································· 13分
 ,可求得点
,可求得点 ;················································ 14分
;················································ 14分
经检验,点 与点
与点 都在抛物线
都在抛物线 上.···························· 16分
上.···························· 16分
054](1)由抛物线经过点A(0,1),C(2,4),
得 解得
解得
∴抛物线对应的函数关系式为: .······························· (2分)
.······························· (2分)
(2)当 时,P点坐标为(1,1),∴Q点坐标为(2,0).
时,P点坐标为(1,1),∴Q点坐标为(2,0).
当 时,P点坐标为(2,3),∴Q点坐标为(5,0).···························· (5分)
时,P点坐标为(2,3),∴Q点坐标为(5,0).···························· (5分)
(3)当 ≤2时,
≤2时, .S
.S .
.
当 ≤5时,
≤5时, .S
.S . (8分)
. (8分)
 当
当 时,S的最大值为2.································································ (10分)
时,S的最大值为2.································································ (10分)
053]解:(1)设 ,把
,把 代入,得
代入,得 ,··························· 2分
,··························· 2分
∴抛物线的解析式为: .顶点
.顶点 的坐标为
的坐标为 .······························· 5分
.······························· 5分
(2)设直线 解析式为:
解析式为: (
( ),把
),把 两点坐标代入,
两点坐标代入,
得 解得
解得 .∴直线
.∴直线 解析式为
解析式为 .······················ 7分
.······················ 7分
 ,∴
,∴ ················ 9分
················ 9分
 .···························································· 10分
.···························································· 10分
∴当 时,
时, 取得最大值,最大值为
取得最大值,最大值为 .······························································ 11分
.······························································ 11分
 (3)当
(3)当 取得最大值,
取得最大值, ,
, ,∴
,∴ .∴四边形
.∴四边形 是矩形.
是矩形.
作点 关于直线
关于直线 的对称点
的对称点 ,连接
,连接 .
.
法一:过 作
作 轴于
轴于 ,
, 交
交 轴于点
轴于点 .
.
设 ,则
,则 .
.
在 中,由勾股定理,
中,由勾股定理, .
.
解得 .∵
.∵ ,∴
,∴ .
.
由 ,可得
,可得 ,
, .∴
.∴ .
.
∴ 坐标
坐标 .································································································ 13分
.································································································ 13分
法二:连接 ,交
,交 于点
于点 ,分别过点
,分别过点 作
作 的垂线,垂足为
的垂线,垂足为 .
.
易证 .
. ∴
∴ .
.
设 ,则
,则 .∴
.∴ ,
, .
.
由三角形中位线定理, .
.
∴ ,即
,即 .
.
 ∴
∴ 坐标
坐标 .······················································· 13分
.······················································· 13分
把 坐标
坐标 代入抛物线解析式,不成立,所以
代入抛物线解析式,不成立,所以 不在抛物线上.·················· 14分
不在抛物线上.·················· 14分
051]解:(1) ,(-1,0),B(3,0).···················· 3分
,(-1,0),B(3,0).···················· 3分
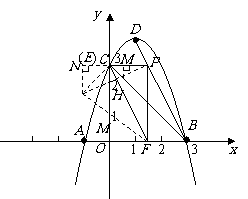
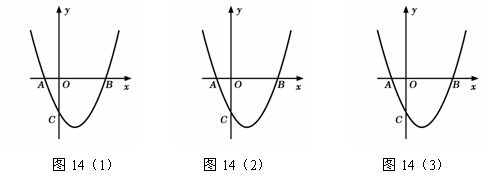
(2)如图14(1),抛物线的顶点为M(1,-4),连结OM.
则 △AOC的面积= ,△MOC的面积=
,△MOC的面积= ,△MOB的面积=6,∴ 四边形 ABMC的面积=△AOC的面积+△MOC的面积+△MOB的面积=9.························································ 6分
,△MOB的面积=6,∴ 四边形 ABMC的面积=△AOC的面积+△MOC的面积+△MOB的面积=9.························································ 6分
 说明:也可过点M作抛物线的对称轴,将四边形ABMC的面
说明:也可过点M作抛物线的对称轴,将四边形ABMC的面
积转化为求1个梯形与2个直角三角形面积的和.
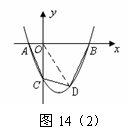
(3)如图14(2),设D(m, ),连结OD.
),连结OD.
则 0<m<3, <0. 且 △AOC的面积=
<0. 且 △AOC的面积= ,△DOC的面积=
,△DOC的面积= ,
,
△DOB的面积=- (
( ),
),
∴ 四边形 ABDC的面积=△AOC的面积+△DOC的面积+△DOB的面积
= =
= .
.
 ∴ 存在点D
∴ 存在点D ,使四边形ABDC的面积最大为
,使四边形ABDC的面积最大为 .
.
(4)有两种情况:
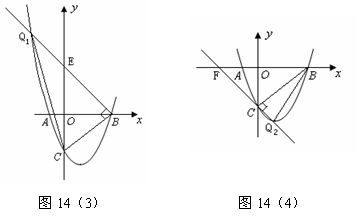
如图14(3),过点B作BQ1⊥BC,交抛物线于点Q1、交y轴于点E,连接Q1C.
∵ ∠CBO=45°,∴∠EBO=45°,BO=OE=3.
∴ 点E的坐标为(0,3). ∴ 直线BE的解析式为 .························· 12分
.························· 12分
由 解得
解得
 ∴ 点Q1的坐标为(-2,5).········ 13分
∴ 点Q1的坐标为(-2,5).········ 13分
如图14(4),过点C作CF⊥CB,交抛物线于点Q2、交x轴于点F,连接BQ2.
∵ ∠CBO=45°,∴∠CFB=45°,OF=OC=3.
∴ 点F的坐标为(-3,0).∴ 直线CF的解析式为 .························ 14分
.························ 14分
由 解得
解得

∴点Q2的坐标为(1,-4).综上,在抛物线上存在点Q1(-2,5)、Q2(1,-4),
使△BCQ1、△BCQ2是以BC为直角边的直角三角形.
 [052]解:(1)根据题意,得
[052]解:(1)根据题意,得
解得 .
. .(2分)
.(2分)
(2)当 时,得
时,得 或
或 ,
,
∵ ,当
,当 时,得
时,得 ,
,
∴ ,∵点
,∵点 在第四象限,∴
在第四象限,∴ .····································· (4分)
.····································· (4分)
当 时,得
时,得 ,∴
,∴ ,
,
∵点 在第四象限,∴
在第四象限,∴ .································································ (6分)
.································································ (6分)
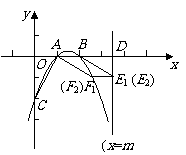
(3)假设抛物线上存在一点 ,使得四边形
,使得四边形 为平行四边形,则
为平行四边形,则
 ,点
,点 的横坐标为
的横坐标为 ,
,
当点 的坐标为
的坐标为 时,点
时,点 的坐标为
的坐标为 ,
,
∵点 在抛物线的图象上,∴
在抛物线的图象上,∴ ,∴
,∴ ,
,
∴ ,∴
,∴ (舍去),∴
(舍去),∴ ,
,
∴ .························································································· (9分)
.························································································· (9分)
当点 的坐标为
的坐标为 时,点
时,点 的坐标为
的坐标为 ,
,
∵点 在抛物线的图象上,∴
在抛物线的图象上,∴ ,∴
,∴ ,
,
∴ ,∴
,∴ (舍去),
(舍去), ,∴
,∴ ,∴
,∴ .
.
051]如图14(1),抛物线 与x轴交于A、B两点,与y轴交于点C(0,
与x轴交于A、B两点,与y轴交于点C(0, ).[图14(2)、图14(3)为解答备用图]
).[图14(2)、图14(3)为解答备用图]
(1) ,点A的坐标为 ,点B的坐标为 ;
,点A的坐标为 ,点B的坐标为 ;
(2)设抛物线 的顶点为M,求四边形ABMC的面积;
的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由;
(4)在抛物线 上求点Q,使△BCQ是以BC为直角边的直角三角形.
上求点Q,使△BCQ是以BC为直角边的直角三角形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com