
2.已知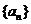 是等差数列,
是等差数列,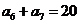 ,
,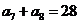 ,则该数列前13项和
,则该数列前13项和 等于
等于
A.156 B.132 C.110 D.100
1.已知全集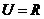 ,则正确表示集合
,则正确表示集合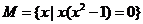 和
和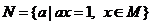 的关系的韦恩(Venn)图是
的关系的韦恩(Venn)图是

A. B. C. D.
050]解:(1)∵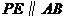
 ∴
∴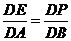 .而
.而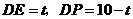 ,
,
∴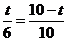 ,∴
,∴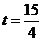 .∴当
.∴当 .
.
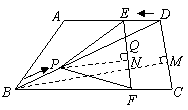
(2)∵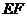 平行且等于
平行且等于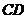 ,
,
∴四边形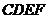 是平行四边形.
是平行四边形.
∴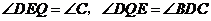 .
.
∵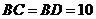 ,∴
,∴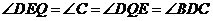 .∴
.∴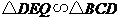 .
.
∴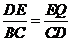 .
.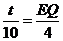 .∴
.∴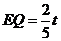 .
.
过B作 ,交
,交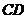 于
于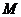 ,过
,过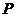 作
作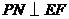 ,交
,交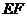 于
于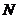 .
.
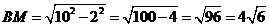 .∵
.∵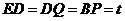 ,
,
∴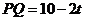 .又
.又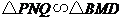 ,
,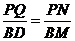 ,
,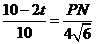 ,
,
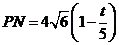 ,
,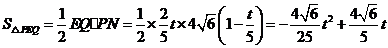 .
.
(3)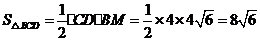 .
.
若 ,则有
,则有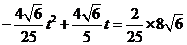 ,解得
,解得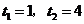 .
.
(4)在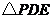 和
和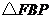 中,
中,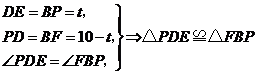
∴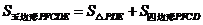

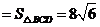 .
.
∴在运动过程中,五边形 的面积不变.
的面积不变.
049]解:(1)由题意得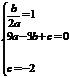 解得
解得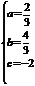
∴此抛物线的解析式为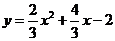 ························································· 3分
························································· 3分
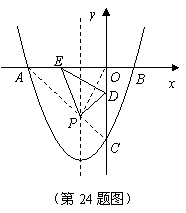
(2)连结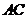 、
、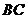 .因为
.因为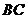 的长度一定,所以
的长度一定,所以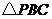 周长最小,就是使
周长最小,就是使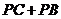 最小
最小 .
.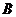 点关于对称轴的对称点是
点关于对称轴的对称点是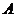 点,
点,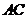 与对称轴
与对称轴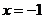 的交点即为所求的点
的交点即为所求的点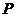 .
.
 设直线
设直线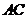 的表达式为
的表达式为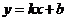 则
则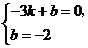 解得
解得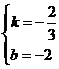
∴此直线的表达式为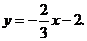
把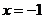 代入得
代入得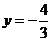 ∴
∴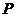 点的坐标为
点的坐标为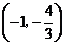
(3)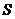 存在最大值,理由:∵
存在最大值,理由:∵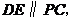 即
即
∴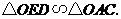 ∴
∴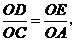 即
即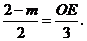
∴
方法一:连结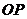 ,
,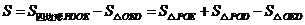
=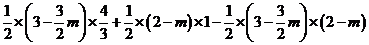 [来源:Z。xx。]
[来源:Z。xx。]
=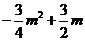 ,∵
,∵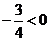 ∴当
∴当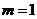 时,
时,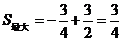 ····················· 9分
····················· 9分
方法二: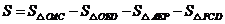
=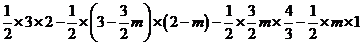
=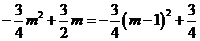 ,∵
,∵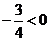 ∴当
∴当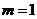 时,
时,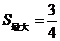 ························· 9分
························· 9分
048]解:(1)由题意得 6=a(-2+3)(-2-1),∴a=-2,
∴抛物线的函数解析式为y=-2(x+3)(x-1)与x轴交于B(-3,0)、A(1,0)
设直线AC为y=kx+b,则有0=k+b,6=-2k+b,解得 k=-2,b=2,
∴直线AC为y=-2x+2
(2)①设P的横坐标为a(-2≤a≤1),则P(a,-2a+2),M(a,-2a2-4a+6)
∴PM=-2a2-4a+6-(-2a+2)=-2a2-2a+4=-2a2+a+14+92
=-2a+122+92,∴当a=-12时,PM的最大值为926分
②M1(0,6)M2-14,678
047]解:方法一:如图(1-1),连接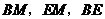 .
.
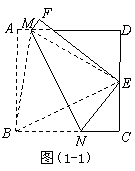
由题设,得四边形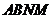 和四边形
和四边形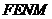 关于直线
关于直线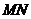 对称.
对称.
∴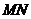 垂直平分
垂直平分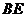 .∴
.∴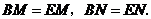 ····················································· 1分
····················································· 1分
∵四边形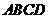 是正方形,∴
是正方形,∴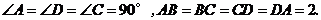
∵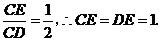 设
设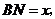 则
则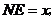
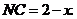
在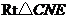 中,
中,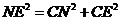 .∴
.∴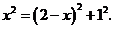 解得
解得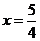 ,即
,即 3分
3分
在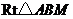 和在
和在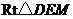 中,
中,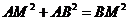 ,
,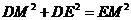 ,
,
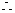
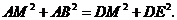 ··················································································· 5分
··················································································· 5分
设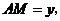 则
则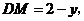 ∴
∴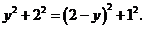
解得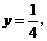 即
即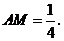 ∴
∴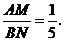 ················································· 7分
················································· 7分
方法二:同方法一, ·················································································· 3分
·················································································· 3分
如图(1-2),过点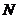 做
做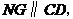 交
交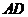 于点
于点 ,连接
,连接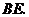
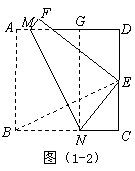
∵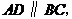 ∴四边形
∴四边形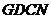 是平行四边形.
是平行四边形.
∴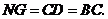
同理,四边形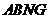 也是平行四边形.∴
也是平行四边形.∴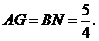
∵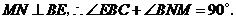
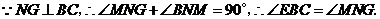
在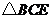 与
与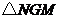 中
中
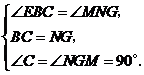 ∴
∴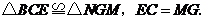 ····························· 5分
····························· 5分
∵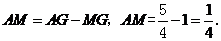 ∴
∴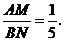 ·········································· 7分
·········································· 7分
类比归纳
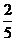 (或
(或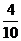 );
);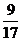 ;
; 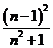
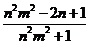 ·················································· 12分
·················································· 12分
046]网](1)解:由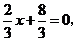 得
得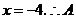 点坐标为
点坐标为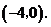
由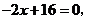 得
得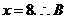 点坐标为
点坐标为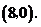 ∴
∴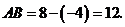 ··································· (2分)
··································· (2分)
由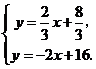 解得
解得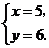 ∴
∴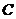 点的坐标为
点的坐标为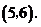 ························································· (3分)
························································· (3分)
∴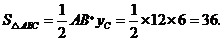 ················································································ (4分)
················································································ (4分)
(2)解:∵点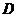 在
在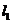 上且
上且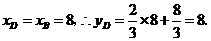
∴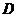 点坐标为
点坐标为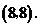 (5分)又∵点
(5分)又∵点 在
在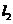 上且
上且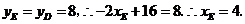
∴ 点坐标为
点坐标为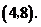 (6分)∴
(6分)∴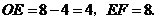 (7分)
(7分)
(3)解法一: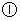 当
当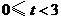 时,如图1,矩形
时,如图1,矩形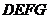 与
与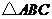 重叠部分为五边形
重叠部分为五边形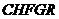 (
(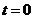 时,为四边形
时,为四边形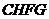 ).过
).过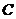 作
作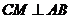 于
于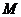 ,则
,则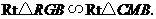
∴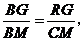 即
即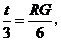 ∴
∴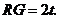
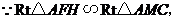
∴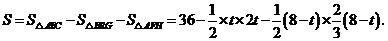
即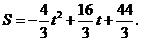
044](1) 配方,得y=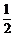 (x–2)2
–1,∴抛物线的对称轴为直线x=2,顶点为P(2,–1) .
(x–2)2
–1,∴抛物线的对称轴为直线x=2,顶点为P(2,–1) .
取x=0代入y=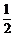 x2 –2x+1,得y=1,∴点A的坐标是(0,1).由抛物线的对称性知,点A(0,1)与点B关于直线x=2对称,∴点B的坐标是(4,1). 2分
x2 –2x+1,得y=1,∴点A的坐标是(0,1).由抛物线的对称性知,点A(0,1)与点B关于直线x=2对称,∴点B的坐标是(4,1). 2分
设直线l的解析式为y=kx+b(k≠0),将B、P的坐标代入,有
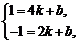 解得
解得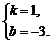 ∴直线l的解析式为y=x–3.3分
∴直线l的解析式为y=x–3.3分
(2) 连结AD交O′C于点E,∵ 点D由点A沿O′C翻折后得到,∴ O′C垂直平分AD.
由(1)知,点C的坐标为(0,–3),∴
在Rt△AO′C中,O ′A=2,AC=4,∴ O′C=2
′A=2,AC=4,∴ O′C=2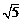 .
.
据面积关系,有 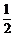 ×O′C×AE=
×O′C×AE=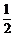 ×O′A×CA,∴ AE=
×O′A×CA,∴ AE=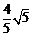 ,AD=2AE=
,AD=2AE=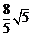 .
.
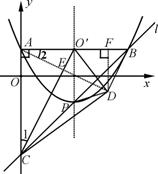
作DF⊥AB于F,易证Rt△ADF∽Rt△CO′A,∴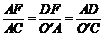 ,
,
 ∴ AF=
∴ AF=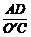 ·AC=
·AC=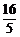 ,DF=
,DF=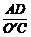 ·O′A=
·O′A= ,5分
,5分
又 ∵OA=1,∴点D的纵坐标为1– = –
= –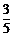 ,
,
∴ 点D的坐标为(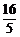 ,–
,–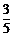 ).
).
(3) 显然,O′P∥AC,且O′为AB的中点,
∴ 点P是线段BC的中点,∴ S△DPC= S△DPB .
故要使S△DQC= S△DPB,只需S△DQC=S△DPC .
过P作直线m与CD平行,则直线m上的任意一点与CD构成的三角形的面积都等于S△DPC ,故m与抛物线的交点即符合条件的Q点.
容易求得过点C(0,–3)、D(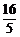 ,–
,–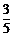 )的直线的解析式为y=
)的直线的解析式为y=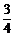 x–3,
x–3,
据直线m的作法,可以求得直线m的解析式为y=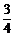 x–
x–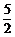 .
.
令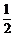 x2–2x+1=
x2–2x+1=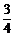 x–
x–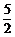 ,解得 x1=2,x2=
,解得 x1=2,x2=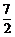 ,代入y=
,代入y=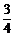 x–
x–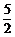 ,得y1= –1,y2=
,得y1= –1,y2= ,
,
因此,抛物线上存在两点Q1(2,–1)(即点P)和Q2(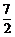 ,
, ),使得S△DQC= S△DPB.
),使得S△DQC= S△DPB.
 [045](1)将A(0,1)、B(1,0)坐标代入
[045](1)将A(0,1)、B(1,0)坐标代入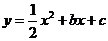 得
得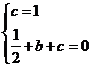 解得
解得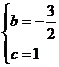
∴抛物线的解折式为 …(2分)
…(2分)
(2)设点E的横坐标为m,则 它的纵坐标为
它的纵坐标为
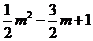
即 E点的坐标(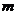 ,
,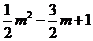 )又∵点E在直线
)又∵点E在直线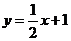 上
上
∴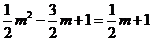 解得
解得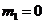 (舍去),
(舍去),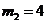
∴E的坐标为(4,3)……(4分)
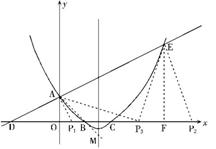
(Ⅰ)当A为直角顶点时
过A作AP1 ⊥DE交x轴于P1点,设P1(a,0) 易知D点坐标为(-2,0) 由Rt△AOD∽Rt△POA得
⊥DE交x轴于P1点,设P1(a,0) 易知D点坐标为(-2,0) 由Rt△AOD∽Rt△POA得
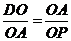 即
即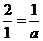 ,∴a=
,∴a=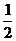 ∴P1(
∴P1(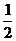 ,0)……(5分)
,0)……(5分)
(Ⅱ)同理,当E为直角顶点时,P2点坐标为(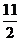 ,0)……(6分)
,0)……(6分)
(Ⅲ)当P为直角顶点时,过E作EF⊥x轴于F,设P3(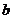 、
、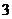 )由∠OPA+∠FPE=90°,得∠OPA=∠FEP Rt△AOP∽Rt△PFE
)由∠OPA+∠FPE=90°,得∠OPA=∠FEP Rt△AOP∽Rt△PFE
由 得
得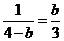 解得
解得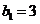 ,
,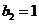
∴此时的点P3的坐标为(1,0)或(3,0)……(8分)
综上所述,满足条件的点P的坐标为(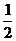 ,0)或(1,0)或(3,0)或(
,0)或(1,0)或(3,0)或(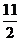 ,0)(Ⅲ)抛物线的对称轴为
,0)(Ⅲ)抛物线的对称轴为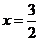 …(9分)∵B、C关于x=
…(9分)∵B、C关于x=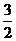 对称 ∴MC=MB
对称 ∴MC=MB
要使 最大,即是使
最大,即是使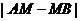 最大
最大
由三角形两边之差小于第三边得,当A、B、M在同一直线上时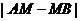 的值最大.易知直线AB的解折式为
的值最大.易知直线AB的解折式为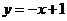 ∴由
∴由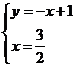 得
得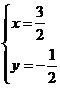
∴M(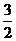 ,-
,-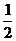 )……(11分)
)……(11分)
043]解(Ⅰ)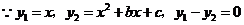 ,
,
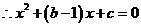 .··························································································· 1分
.··························································································· 1分
将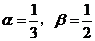 分别代入
分别代入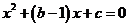 ,得
,得
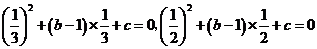 ,
,
解得 .
.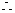 函数
函数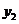 的解析式为
的解析式为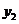
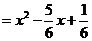 .································· 3分
.································· 3分
(Ⅱ)由已知,得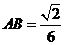 ,设
,设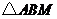 的高为
的高为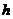 ,
,
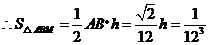 ,即
,即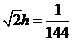 .
.
根据题意,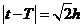 ,由
,由 ,得
,得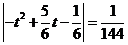 .
.
当 时,解得
时,解得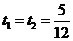 ;
;
当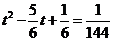 时,解得
时,解得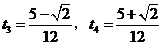 .
.
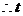 的值为
的值为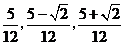 .··············································································· 6分
.··············································································· 6分
(Ⅲ)由已知,得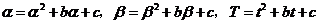 .
.
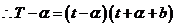 ,
,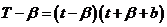 ,
,
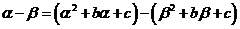 ,化简得
,化简得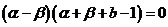 .
.
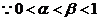 ,得
,得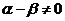 ,
,  .
.
有
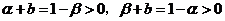 .
.
又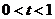 ,
, ,
,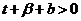 ,
,
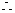 当
当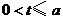 时,
时, ;当
;当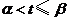 时,
时,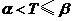 ;
;
当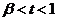 时,
时, .························································································· 10分
.························································································· 10分
042]解:(1)∵点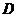 是
是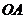 的中点,∴
的中点,∴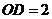 ,∴
,∴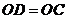 .
.
又∵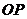 是
是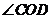 的角平分线,∴
的角平分线,∴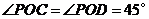 ,
,
∴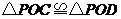 ,∴
,∴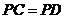 .········································································· 3分
.········································································· 3分
(2)过点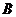 作
作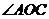 的平分线的垂线,垂足为
的平分线的垂线,垂足为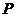 ,点
,点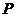 即为所求.
即为所求.
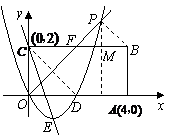 易知点
易知点 的坐标为(2,2),故
的坐标为(2,2),故 ,作
,作 ,
,
∵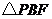 是等腰直角三角形,∴
是等腰直角三角形,∴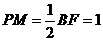 ,
,
∴点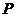 的坐标为(3,3).
的坐标为(3,3).
∵抛物线经过原点,∴设抛物线的解析式为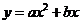 .
.
又∵抛物线经过点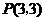 和点
和点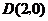 ,∴有
,∴有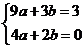 解得
解得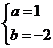
∴抛物线的解析式为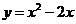 .··············································································· 7分
.··············································································· 7分
(3)由等腰直角三角形的对称性知D点关于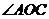 的平分线的对称点即为
的平分线的对称点即为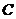 点.
点.
连接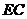 ,它与
,它与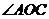 的平分线的交点即为所求的
的平分线的交点即为所求的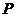 点(因为
点(因为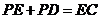 ,而两点之间线段最短),此时
,而两点之间线段最短),此时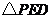 的周长最小.
的周长最小.
∵抛物线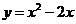 的顶点
的顶点 的坐标
的坐标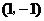 ,
,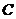 点的坐标
点的坐标 ,
,
设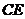 所在直线的解析式为
所在直线的解析式为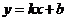 ,则有
,则有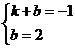 ,解得
,解得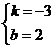 .
.
∴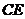 所在直线的解析式为
所在直线的解析式为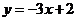 .
.
点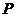 满足
满足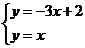 ,解得
,解得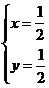 ,故点
,故点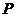 的坐标为
的坐标为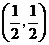 .
.
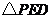 的周长即是
的周长即是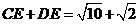 .
.
(4)存在点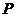 ,使
,使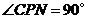 .其坐标是
.其坐标是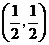 或
或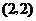 .································· 14分
.································· 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com