
1.在抽查某产品的尺寸过程中,将其尺寸分成若干组,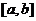 是其中一组,抽查出的个体数在该组上的频率为
是其中一组,抽查出的个体数在该组上的频率为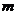 ,该组上的直方图的高为
,该组上的直方图的高为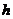 ,则
,则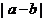 等于
( )
等于
( )
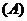
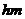
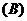
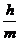
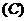
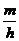
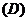 与
与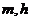 无关
无关
2. 试这些数据分析该居民区居民的消费状况,并作出居民区消费能力的总体评价。
|
居民月消费支出额分组上限 |
|
|||
|
频数 |
累计频数 |
频率(%) |
累计频率(%) |
|
|
[800,900) |
5 |
|
|
|
|
[900,1000) |
1 |
|
|
|
|
[1000,1100) |
8 |
|
|
|
|
[1100,1200) |
11 |
|
|
|
|
[1200,1300) |
11 |
|
|
|
|
[1300,1400) |
7 |
|
|
|
|
[1400,1500) |
4 |
|
|
|
|
[1500,1600) |
2 |
|
|
|
|
[1600,1700) |
1 |
|
|
|
|
合 计 |
50 |
~ |
100 |
~ |
|
居民月消费支出额分组上限 |
|
|||
|
频数 |
累计频数 |
频率(%) |
累计频率(%) |
|
|
[800,900) |
5 |
5 |
10 |
10 |
|
[900,1000) |
1 |
6 |
2 |
12 |
|
[1000,1100) |
8 |
14 |
16 |
28 |
|
[1100,1200) |
11 |
25 |
22 |
50 |
|
[1200,1300) |
11 |
36 |
22 |
72 |
|
[1300,1400) |
7 |
43 |
14 |
86 |
|
[1400,1500) |
4 |
47 |
8 |
94 |
|
[1500,1600) |
2 |
49 |
4 |
98 |
|
[1600,1700) |
1 |
50 |
2 |
100 |
|
合 计 |
50 |
~ |
100 |
~ |
解:
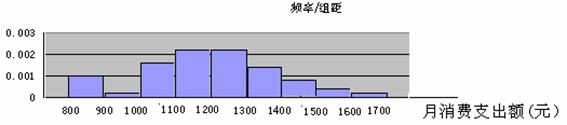
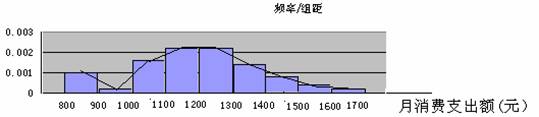
例2:下面一组数据是某生产车间30名工人某日加工零件的个数,请设计适当的茎叶图表示这组数据,并由图出发说明一下这个车间此日的生产情况。
|
134 |
112 |
117 |
126 |
128 |
124 |
122 |
116 |
113 |
107 |
|
116 |
132 |
127 |
128 |
126 |
121 |
120 |
118 |
108 |
110 |
|
133 |
130 |
124 |
116 |
117 |
123 |
122 |
120 |
112 |
112 |
分析:以零件个数的前两位数作茎,后一位数作叶。
 解:
解:
从图可以看出这个车间此日的零件生产数目平均每人120左右。
点评:用茎叶图表示有两个突出的优点,其一,从统计图上没有信息的损失,所有的信息都可以从这个茎叶图中得到;其二,茎叶图可以在比赛时随时记录,方便记录与表示。但茎叶图只能表示两位的整数,虽然可以表示两个人以上的比赛结果(或两个以上的记录),但没有表示两个记录那么直观、清晰。
[同步训练]
1. 完成下面的分布表并根据下表画出频率分布直方图、折线图。
2.经典回放:
例1:为调查某居民区居民的购买消费品的支出情况,特从中抽出了50户并对其实际消费进行了如下的统计:
某市50户居民某月购买消费品支出情况表 单位:元
|
按户月消费品支出额分组 |
频数 |
频率 |
|
800-900 900-1000 1000-1100 1100-1200 1200-1300 1300-1400 1400-1500 1500以上 |
5 1 8 11 11 7 4 3 |
0.10 0.02 0.16 0.22 0.22 0.14 0.08 0.06 |
|
合 计 |
50 |
1.00 |
1.解析视屏:
(1)频率折线图:将频率分布直方图中各相邻矩形的上底边中点顺次连接起来就得到一条折线,这条折线成为本组数据的频率折线图。
(2)总体密度曲线:样本容量越大,所分组数越多,各组的频率就接近于总体在相应各组的取值概率,设想样本容量无限大,分组的组距无限缩小,频率分布的直方图就会接近于一条曲线--总体密度曲线,它反映了总体在各个范围内取值的概率。根据这条曲线,可求出总体在区间(a,b)内取值的概率等于总体密度曲线,直线x=a,x=b及x轴所围图形的面积.
(3)茎叶图:它的思路是将数组的数按位数进行比较,将数大小基本不变或变化不大的位作为一个主杆(茎),将变化大的位的数作为分枝(叶),列在主杆的后面,这样就可以清楚地看到每个主杆后面的几个数,每个数具体是多少。
茎叶图有三列数:左边的一列数统计数,它是上(或下)向中心累积的值,中心的数(带括号)表示最多数组的个数;中间的一列表示茎,也就是变化不大的位数;右边的是数组中的变化位,它是按照一定的间隔将数组中的每个变化的数一一列出来,象一条枝上抽出的叶子一样,所以人们形象地叫它茎叶图。
茎叶图在质量管理上用途与直方图差不多,但它通常是作为更细致的分析阶段使用。它是用数字组成直方图。
2.学法指导:
频率分布表、频率分布直方图、总体密度曲线三者的关系,就好比在函数学习中函数表示法中的列表、描点、连线三个层次,是不断进步的一种表示方法。频率折线图能反映发展变化的趋势,茎叶图能直观地反映出数据的水平状况、稳定程度。
[教师在线]
1.学习目标:
掌握折线图表示样本的分布情况,掌握茎叶图的制作方法明白茎叶图的具体含义,会作茎叶图来分析数据的分布状况。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com