
15.已知函数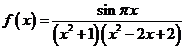 .
.
(Ⅰ)方程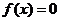 在区间
在区间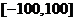 上实数解的个数是__________;
上实数解的个数是__________;
(Ⅱ)对于下列命题:① 函数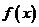 是周期函数;
是周期函数;
② 函数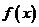 既有最大值又有最小值;
既有最大值又有最小值;
③ 函数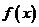 的定义域是R,且其图象有对称轴;
的定义域是R,且其图象有对称轴;
④对于任意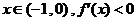 (
(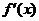 是函数
是函数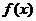 的导函数).
的导函数).
其中真命题的序号是 .(填写出所有真命题的序号)
15答案: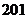 ;②③
;②③
解析:(Ⅰ)由于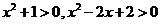 ,故
,故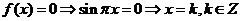
在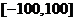 中的整数个数
中的整数个数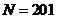
故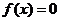 在区间
在区间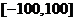 上实数解的个数为
上实数解的个数为 .
.
(Ⅱ)命题①:由分母为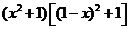 ,易知
,易知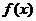 不是周期函数,故为假命题;
不是周期函数,故为假命题;
命题②:由于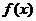 是
是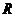 上的连续函数,且
上的连续函数,且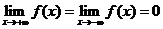 ,可知
,可知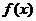 既有最大值又有最小值,故为真命题;
既有最大值又有最小值,故为真命题;
命题③:由于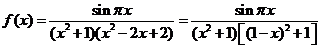 ,故
,故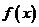 的定义域是R
的定义域是R
看到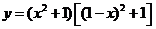 的对称轴为
的对称轴为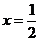 ,且
,且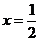 为
为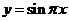 的一条对称轴
的一条对称轴
故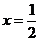 为
为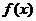 图象的对称轴,故为真命题;
图象的对称轴,故为真命题;
命题④:由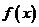 在定义域R上连续,且
在定义域R上连续,且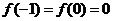 ,可知
,可知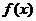 不可能在
不可能在 上为减函数,故为假命题.
上为减函数,故为假命题.
14.已知数列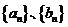 都是公差为
都是公差为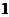 的等差数列,其首项分别为
的等差数列,其首项分别为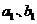 ,且
,且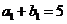 ,
,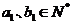 .设
.设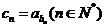 ,则数列
,则数列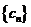 的前
的前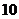 项和为
.
项和为
.
14答案: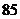
解析:设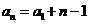 ,
,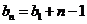 ,则
,则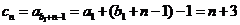 .
.
所以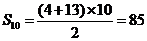 .
.
13.已知函数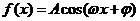 的图象如
的图象如
图所示,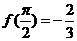 ,则
,则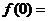 .
.
13答案: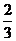
解析:由图象可得最小正周期为 .
.
所以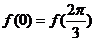 ,注意到
,注意到 与
与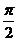 关于
关于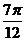 对称,故
对称,故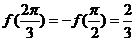 .
.
12.已知向量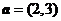 ,
,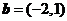 ,则
,则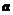 在
在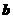 方向上的投影等于 .
方向上的投影等于 .
12答案: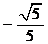
 解析:
解析: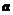 在
在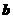 方向上的投影为
方向上的投影为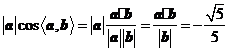 .
.
11.已知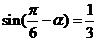 ,则
,则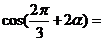 .
.
11答案: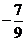 .
.
解析: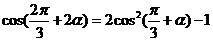 ,且
,且
所以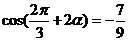 .
.
10.数列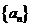 满足
满足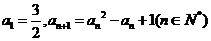 ,则
,则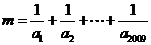 的整数部分是
的整数部分是
A.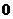 B.
B.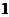 C.
C.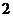 D.
D.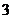
10答案:B
解析:由题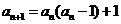 ,则
,则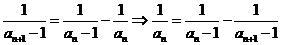 ,故有
,故有
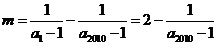 ,由于
,由于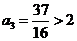 且
且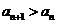 ,故
,故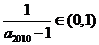 ,所以
,所以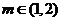 ,其整数部分是
,其整数部分是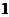 .
.
9.设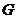 是
是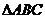 的重心,且
的重心,且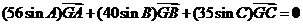 ,则
,则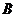 的大小为
的大小为
A.45° B.60° C.30° D.15°
9答案:B
解析:由重心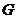 满足
满足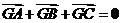 知,
知,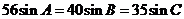
同时由正弦定理,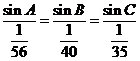 ,故可令三边长
,故可令三边长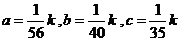
取 ,则
,则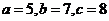 ,借助余弦定理求得
,借助余弦定理求得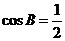 .
.
8.已知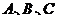 是锐角
是锐角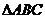 的三个内角,向量
的三个内角,向量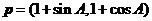 ,
,
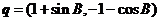 ,则
,则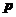 与
与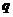 的夹角是
的夹角是
A.锐角 B.钝角 C.直角 D.不确定
8答案:A
解析:锐角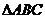 中,
中,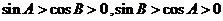 ,
,
故有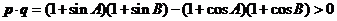 ,同时易知
,同时易知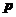 与
与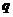 方向不相同,故
方向不相同,故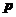 与
与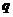 的夹角是锐角.
的夹角是锐角.
7.已知函数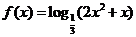 ,则
,则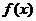 的单调增区间为
的单调增区间为
A. B.
B.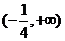 C.
C. D.
D.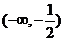
7答案:D
解析:令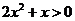 且
且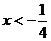 ,即得
,即得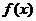 的单调增区间为
的单调增区间为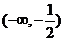 .
.
6.同时具有性质:“①最小正周期为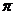 ;②图象关于直线
;②图象关于直线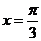 对称;③在
对称;③在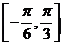 上是增函数”的一个函数是
上是增函数”的一个函数是
A.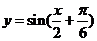 B.
B.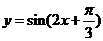
C.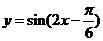 D.
D.
6答案:C
解析:逐一排除即可.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com