
4.下列带电粒子经过电压为U的电压加速后,如果它们的初速度均为0,则获得速度最大的粒子是 ( )
A.质子 B.氚核 C.氦核 D.钠离子Na+
3.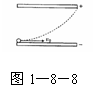 电子从负极板的边缘垂直进入匀强电场,恰好从正极板边缘飞出,如图1-8-8所示,现在保持两极板间的电压不变,使两极板间的距离变为原来的2倍,电子的入射方向及位臀不变,且要电子仍从正极板边缘飞出,则电子入射的初速度大小应为原来的( )
电子从负极板的边缘垂直进入匀强电场,恰好从正极板边缘飞出,如图1-8-8所示,现在保持两极板间的电压不变,使两极板间的距离变为原来的2倍,电子的入射方向及位臀不变,且要电子仍从正极板边缘飞出,则电子入射的初速度大小应为原来的( )
A.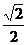 B.
B.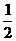 C.
C.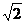 D.2
D.2
2.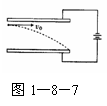 如图1-8-7所示,两极板与电源相连接,电子从负极板边缘垂直电场方向射入匀强电场,且恰好从正极板边缘飞出,现在使电子入射速度变为原来的两倍,而电子仍从原位置射入,且仍从正极板边缘飞出,则两极板的间距应变为原来的
( )
如图1-8-7所示,两极板与电源相连接,电子从负极板边缘垂直电场方向射入匀强电场,且恰好从正极板边缘飞出,现在使电子入射速度变为原来的两倍,而电子仍从原位置射入,且仍从正极板边缘飞出,则两极板的间距应变为原来的
( )
A.2倍 B.4倍
C.0.5倍 D.0.25倍
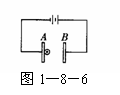
1.如图l-8-6所示,电子由静止开始从A板向B板运动,当到达B板时速度为v,保持两板间电压不变.则 ( )
A.当增大两板间距离时,v也增大
B.当减小两板间距离时,v增大
C.当改变两板间距离时,v不变
D.当增大两板间距离时,电子在两板间运动的时间延长
6.带电粒子在电场中的运动
(1)带电粒子在电场中的运动由粒子的初始状态和受力情况决定.在非匀强电场中,带电粒子受到的电场力是变力,解决这类问题可以用动能定理求解.在匀强电场中,带电粒子受到的是恒力,若带电粒子初速度为零或初速度方向平行于电场方向,带电粒子将做匀变速直线运动;若带电粒子初速度方向垂直于电场方向,带电粒子做类平抛运动,根据运动规律求解,
(2)带电小球、带电微粒(重力不能忽略)在匀强电场中运动,由于带电小球、带电微粒可视为质点,同时受到重力和电场力的作用,其运动情况由重力和电场力共同决定.又因为重力和电场力都是恒力,其做功特点一样,常将带电质点的运动环境想象成一等效场,等效场的大小和方向由重力场和电场共同决定.
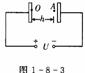 例2两平行金属板相距为d,电势差为U,一电子质量为m,电荷量为e,从O点沿垂直于极板的方向射出,最远到达A点,然后返回,如图1-8-3所示,OA=h,此电子具有的初动能是
( )
例2两平行金属板相距为d,电势差为U,一电子质量为m,电荷量为e,从O点沿垂直于极板的方向射出,最远到达A点,然后返回,如图1-8-3所示,OA=h,此电子具有的初动能是
( )
A.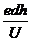 B.edUh
B.edUh
C.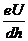 D.
D.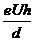
解析:电子从O点到A点,因受电场力作用,速度逐渐减小,根据题意和图示可知,电子仅受电场力,由能量关系: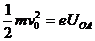 ,又E=U/d,
,又E=U/d,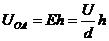 ,所以
,所以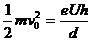 . 故D正确.
. 故D正确.
点评:应用电场力做功与电势差的关系,结合动能定理即可解答本题.
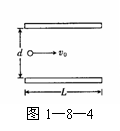
例3一束质量为m、电荷量为q的带电粒子以平行于两极板的速度v0进入匀强电场,如图1-8-4所示.如果两极板间电压为U,两极板间的距离为d、板长为L.设粒子束不会击中极板,则粒子从进入电场到飞出极板时电势能的变化量为 .(粒子的重力忽略不计)
分析:带电粒子在水平方向做匀速直线运动,在竖直方向做匀加速运动.电场力做功导致电势能的改变.
 解析:水平方向匀速,则运动时间t =L/ v0
①
解析:水平方向匀速,则运动时间t =L/ v0
①
竖直方向加速,则侧移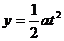 ②
②
且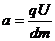 ③
③
由①②③得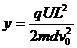
则电场力做功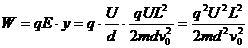
由功能原理得电势能减少了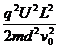
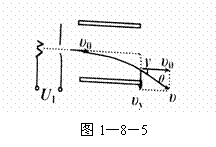
例4如图1-8-5所示,离子发生器发射出一束质量为m,电荷量为q的离子,从静止经加速电压U1加速后,获得速度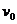 ,并沿垂直于电场线方向射入两平行板中央,受偏转电压U2作用后,以速度
,并沿垂直于电场线方向射入两平行板中央,受偏转电压U2作用后,以速度 离开电场,已知平行板长为
离开电场,已知平行板长为 ,两板间距离为d,求:
,两板间距离为d,求:
 ①
①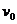 的大小;
的大小;
②离子在偏转电场中运动时间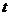 ;
;
③离子在偏转电场中受到的电场力的大小F;
④离子在偏转电场中的加速度;
⑤离子在离开偏转电场时的横向速度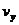 ;
;
⑥离子在离开偏转电场时的速度 的大小;
的大小;
⑦离子在离开偏转电场时的横向偏移量y;
⑧离子离开偏转电场时的偏转角θ的正切值tgθ
解析:①不管加速电场是不是匀强电场,W=qU都适用,所以由动能定理得:
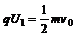
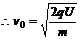
②由于偏转电场是匀强电场,所以离子的运动类似平抛运动.
即:水平方向为速度为v0的匀速直线运动,竖直方向为初速度为零的匀加速直线运动.
∴在水平方向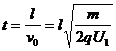
③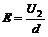 F=qE=
F=qE=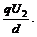
④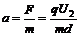
⑤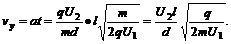
⑥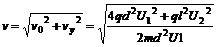
⑦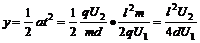 (和带电粒子q、m无关,只取决于加速电场和偏转电场)
(和带电粒子q、m无关,只取决于加速电场和偏转电场)
解题的一般步骤是:
(1)根据题目描述的物理现象和物理过程以及要回答问题,确定出研究对象和过程.并选择出“某个状态”和反映该状态的某些“参量”,写出这些参量间的关系式.
(2)依据题目所给的条件,选用有关的物理规律,列出方程或方程组,运用数学工具,对参量间的函数关系进行逻辑推理,得出有关的计算表达式.
(3)对表达式中的已知量、未知量进行演绎、讨论,得出正确的结果.
 [同步检测]
[同步检测]
5.易错易混点
带电粒子在电场中发生偏转,-定要区分开位移的方向与速度的方向,它们各自偏角的正切分别为:
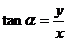 ,
,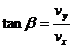 ,切不可混淆
,切不可混淆
4.在带电粒子的加速或偏转的问题中,何时考虑粒子的重力?何时不计重力?
一般来说:(1)基本粒子:如电子、质子、α粒子、离子等除有特别说明或有明确暗示以外,一般都不考虑重力(但不忽略质量).
(2)带电颗粒:如液滴、油滴、尘埃、小球等,除有特别说明或有明显暗示以外,一般都不能忽略重力.
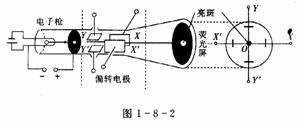
3.示波管的原理
(1)构造及功能如图l-8-2所示
①电子枪:发射并加速电子.
②偏转电极YY,:使电子束竖直偏转(加信号电压) XX,:使电子束水平偏转(加扫描电压).
③荧光屏.
(2)工作原理(如图1-8-2所示)
偏转电极XX,和YY,不加电压,电子打到屏幕中心;若电压只加XX,,只有X方向偏;若电压只加YY,,只有y方向偏;若XX,加扫描电压,YY,加信号电压,屏上会出现随信号而变化的图象.
2.带电粒子的偏转
(1)动力学分析:带电粒子以速度v0垂直于电场线方向飞入两带电平行板产生的匀强电场中,受到恒定的与初速度方向成900角的电场力作用而做匀变速曲线运动 (类平抛运动).
(2)运动的分析方法(看成类平抛运动):
①沿初速度方向做速度为v0的匀速直线运动.
②沿电场力方向做初速度为零的匀加速直线运动.
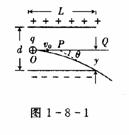
例1如图1-8-1所示,两板间电势差为U,相距为d,板长为L.-正离子q以平行于极板的速度v0射入电场中,在电场中受到电场力而发生偏转,则电荷的偏转距离y和偏转角θ为多少?
 解析:电荷在竖直方向做匀加速直线运动,受到的力F=Eq=Uq/d
解析:电荷在竖直方向做匀加速直线运动,受到的力F=Eq=Uq/d
由牛顿第二定律,加速度a = F/m = Uq/md
水平方向做匀速运动,由L = v0t得t = L/ v0
由运动学公式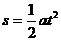 可得:
可得: 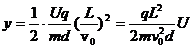
带电离子在离开电场时,竖直方向的分速度:v⊥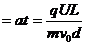
离子离开偏转电场时的偏转角度θ可由下式确定: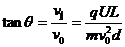
电荷射出电场时的速度的反向延长线交两板中心水平线上的位置确定:如图所示,设交点P到右端Q的距离为x,则由几何关系得: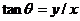
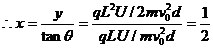
点评:电荷好像是从水平线OQ中点沿直线射出一样,
注意此结论在处理问题时应用很方便.
1.带电粒子的加速
(1)动力学分析:带电粒子沿与电场线平行方向进入电场,受到的电场力与运动方向在同一直线上,做加(减)速直线运动,如果是匀强电场,则做匀加(减)速运动.
(2)功能关系分析:粒子只受电场力作用,动能变化量等于电势能的变化量.
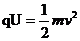 (初速度为零);
(初速度为零);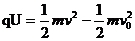 此式适用于一切电场.
此式适用于一切电场.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com