
4.下图表示细胞中的五类有机化合物的关系,每个椭圆形代表一种有机物,下面列出这五种化合物名称中最合理的一组是
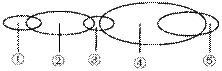 A.①-⑤:维生素、脂质、酶、蛋白质、激素
A.①-⑤:维生素、脂质、酶、蛋白质、激素
B.①-⑤:酶、蛋白质、激素、脂质、维生素
C.①-⑤:维生素、脂质、激素、蛋白质、酶
D.①-⑤:激素、脂质、维生素、蛋白质、酶
3.下列各组物质的基本组成单位相同的是
A.细菌的质粒和基因 B.动物的糖原和抗原
C.人的胰岛素和性激素 D.植物的纤维素和生长素
2.若“淀粉一麦芽糖一葡萄糖一糖元”表示某生物体内糖类的某些转化过程,则下列说法正确的是
①此生物是动物,因为能将淀粉转化为糖元 ②上述关于糖的转化不可能发生在同一生物体内,因为淀粉和麦芽糖是植物特有的糖,而糖元是动物特有的糖 ③此生物一定是植物,因为它能利用淀粉和麦芽糖④淀粉和糖元都是储存能量的多糖,麦芽糖为二糖,葡萄糖为单糖
A.②③ B.①④ C.①③④ D.①②④
1.下列化合物均含N元素的一组是
A.血红蛋白和核酸 B.纤维素和核苷酸 C.葡萄糖和脂肪酸 D.乳糖和淀粉酶
21.(本小题14分)
已知函数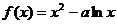 在(1,2]上是增函数。
在(1,2]上是增函数。
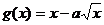 在(0,1)上减函数。
在(0,1)上减函数。
(1)求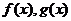 的表达式。
的表达式。
(2)当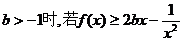 在
在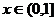 内恒成立,求实数
内恒成立,求实数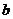 的取值范围。
的取值范围。
(3)求证:当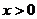 时,方程
时,方程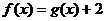 有唯一解。
有唯一解。

 安徽省无为中学(2009-2010-1)第二次检测试卷
安徽省无为中学(2009-2010-1)第二次检测试卷
20.(本小题13分)
对于三次函数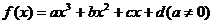

 定义:
定义:
(1)设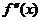 是函数
是函数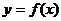 的导函数
的导函数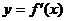 的导数。若方程
的导数。若方程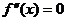 有实数解
有实数解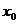 ,则称点
,则称点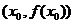 为函数
为函数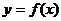 的“拐点”。
的“拐点”。
(2)设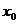 为常数,若定义在R上的函数
为常数,若定义在R上的函数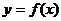 对于定义域内的一切实数
对于定义域内的一切实数 ,都有
,都有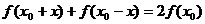 成立。则函数
成立。则函数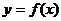 的图象关于点
的图象关于点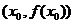 对称
对称
已知:
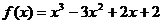
(1)求函数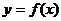 的“拐点”A的坐标。
的“拐点”A的坐标。
(2)检验函数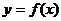 的图象是否关于“拐点”A对称。并对任意一个三次函数,写出一个有关“拐点”的结论(不必证明)
的图象是否关于“拐点”A对称。并对任意一个三次函数,写出一个有关“拐点”的结论(不必证明)
(3)写出一个三次函数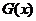 ,使它的“拐点”为(-1,3),(不写过程)
,使它的“拐点”为(-1,3),(不写过程)
19.(本小题12分)已知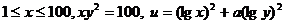
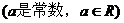 ①写出
①写出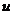 关于
关于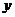 的函数解析式。
的函数解析式。
② 求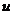 的最大值与最小值。
的最大值与最小值。
18.(本小题12分),在△ABC中,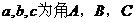 的对边,已知
的对边,已知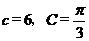
①△ABC的面积为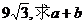
②若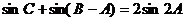 ,求△ABC的面积
,求△ABC的面积
17.(本小题12分)设二次函数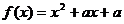 方程
方程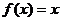 的两根为
的两根为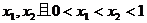
(1)求实数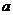 的范围
的范围
(2)试比较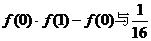 的大小,并说明理由。
的大小,并说明理由。
16.(本小题12分),已知函数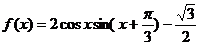
(1)求函数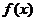 的最小正周期
的最小正周期
(2)在给定的坐标系中,作出函数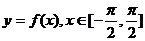 的图象。
的图象。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com