
18.(本题满分16分,第1小题10分,第2小题6分)
在直角坐标系 中,椭圆
中,椭圆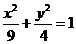 的左、右焦点分别为
的左、右焦点分别为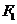 、
、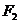 ,点
,点 为椭圆的左顶点,椭圆上的点
为椭圆的左顶点,椭圆上的点 在第一象限,
在第一象限, ,
,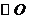 的方程为
的方程为
(1) 求点 坐标,并判断直线
坐标,并判断直线 与
与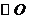 的位置关系;
的位置关系;
(2) 是否存在不同于点 的定点
的定点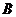 ,对于
,对于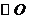 上任意一点
上任意一点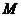 ,都有
,都有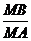 为常数,若存在,求所以满足条件的点
为常数,若存在,求所以满足条件的点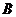 的坐标;若不存在,说明理由。
的坐标;若不存在,说明理由。
17.(本题满分14分,第1小题8分,第2小题6分)
某品牌茶壶的原售价为80元/个,今有甲、乙两家茶具店销售这种茶壶,甲店用如下方法促销:如果只购买一个茶壶,其价格为78元/个;如果一次购买两个茶壶,其价格为76元/个;… …,一次购买的茶壶数每增加一个,那么茶壶的价格减少2元/个,但茶壶的售价不得低于44元/个;乙店一律按原价的75℅销售。现某茶社要购买这种茶壶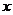 个,如果全部在甲店购买,则所需金额为
个,如果全部在甲店购买,则所需金额为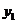 元;如果全部在乙店购买,则所需金额为
元;如果全部在乙店购买,则所需金额为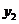 元。
元。
(1) 分别求出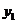 、
、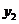 与
与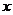 之间的函数关系式;
之间的函数关系式;
(2) 该茶社去哪家茶具店购买茶壶花费较少?
16.(本题满分14分,第1小题7分,第2小题7分)
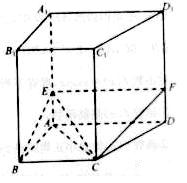
如图,直四棱柱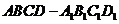 中,四边形
中,四边形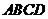 是梯形,
是梯形,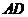 //
//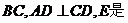
 上的一点。
上的一点。
(1) 求证: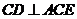 ;
;
(2) 若平面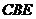 交
交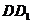 于点
于点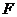 ,求证:
,求证:
15.(本题满分14分)
已知 为锐角,
为锐角, ,求
,求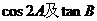 的值。
的值。
14.正整数按下列方法分组: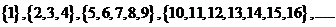 记第
记第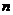 组中各数之和为
组中各数之和为 ;由自然数的立方构成下列数组:
;由自然数的立方构成下列数组: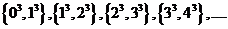 记第
记第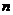 组中后一个数与前一个数的差为
组中后一个数与前一个数的差为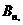 则
则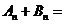 __________
__________
13.对函数 ,现有下列命题:
,现有下列命题:
①函数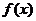 是偶函数
是偶函数
②函数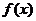 的最小正周期是
的最小正周期是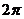
③点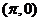 是函数
是函数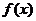 的图象的一个对称中学;
的图象的一个对称中学;
④函数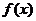 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减。
上单调递减。
其中是真命题的是__________ (写出所有真命题的序号)。
12.如图,平面四边形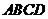 中,
中,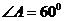 ,
, ,
,

11.设直线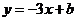 是曲线
是曲线 的一条切线,则实数
的一条切线,则实数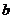 的值是__________
的值是__________
10.在直角坐标系 中,双曲线
中,双曲线 的左准线为
的左准线为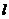 ,则以
,则以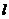 为准线的抛物线的标准方程是__________ 。
为准线的抛物线的标准方程是__________ 。
9.已知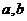 都是单位向量,
都是单位向量,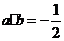 ,则
,则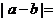 __________
__________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com