2．二元二次方程是圆方程的充要条件

　“A=C≠0且B=0”是一个一般的二元二次方程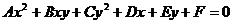表示圆的必要条件．

　二元二次方程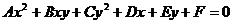表示圆的充要条件为“A=C≠0、B=0且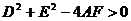”，它可根据圆的一般方程推导而得．

2. 圆

　(1)圆方程的三种形式

　标准式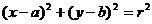：，其中点(a，b)为圆心，r>0，r为半径，圆的标准方程中有三个待定系数，使用该方程的最大优点是可以方便地看出圆的圆心坐标与半径的大小．

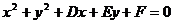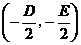　一般式：，其中为圆心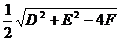为半径，，圆的一般方程中也有三个待定系数，即D、E、F．若已知条件中没有直接给出圆心的坐标(如题目为：已知一个圆经过三个点，求圆的方程)，则往往使用圆的一般方程求圆方程．

　参数式：以原点为圆心、r为半径的圆的参数方程是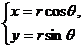(其中θ为参数)．

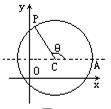　以(a，b)为圆心、r为半径的圆的参数方程为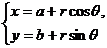(θ为参数)，θ的几何意义是：以垂直于y轴的直线与圆的右交点A与圆心C的连线为始边、以C与动点P的连线为终边的旋转角，如图所示．

　三种形式的方程可以相互转化，其流程图为：

1．直线

(1).直线的倾斜角和斜率

直线的的斜率为k，倾斜角为α，它们的关系为：k＝tanα；

若A(x₁,y₁)，B(x₂,y₂)，则。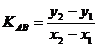

(2) .直线的方程

a.点斜式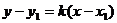：；　 b.斜截式：；

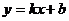c.两点式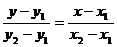：；　 d.截距式：；

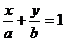e.一般式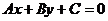：，其中A、B不同时为0.

　(3).两直线的位置关系

两条直线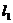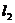，有三种位置关系：平行(没有公共点)；相交(有且只有一个公共点)；重合(有无数个公共点).在这三种位置关系中，我们重点研究平行与相交。

若直线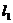、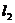的斜率分别为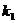、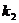，则

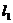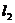
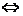
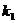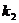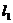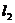
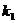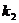∥＝，⊥·＝－1。

(4)点、直线之间的距离

点A(x₀，y₀)到直线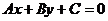的距离为：d=。

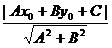两点之间的距离：|AB|=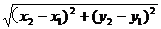

6．强化“分类思想”应用。指数函数与对数函数的性质均与其底数是否大于1有关；对于根式的意义及其性质的讨论要分清n是奇数还是偶数等。

5．实施“定义域优先”原则。函数的定义域是函数最基本的组成部分，任何对函数性质的研究都离不开函数的定义域。例如，求函数的单调区间，必须在定义域范围内；通过求出反函数的定义域，可得到原函数的值域；定义域关于原点对称，是函数为奇函数或偶函数的必要条件。为此，应熟练掌握求函数定义域的原则与方法，并贯彻到解题中去。

4．重视“数形结合”渗透。“数缺形时少直观，形缺数时难入微”。当你所研究的问题较为抽象时，当你的思维陷入困境时，当你对杂乱无章的条件感到头绪混乱时，一个很好的建议便是：画个图!利用图形的直观性，可迅速地破解问题，乃至最终解决问题。

3．活用“定义法”解题。定义是一切法则与性质的基础，是解题的基本出发点。利用定义，可直接判断所给的对应是否满足映射或函数的条件，证明或判断函数的单调性与奇偶性并写出函数的单调区间等。

2．涉及本单元知识点的高考题，综合性大题不多．所以在复习中不宜做过多过高的要求，只要灵活掌握小型综合题型(如集合与映射，集合与自然数集，集合与不等式，集合与方程等，充分条件与必要条件与三角、立几、解几中的知识点的结合等) 映射的概念以选择题型出现，难度不大。就可以了

1．在复习中首先把握基础性知识，深刻理解本单元的基本知识点、基本数学思想和基本数学方法．重点掌握集合、充分条件与必要条件的概念和运算方法．要真正掌握数形结合思想--用文氏图解题．

(二)2010年高考预测

1．集合是每年高考必考的知识点之一。题型一般是选择和填空的形式，主要考查集合的运算和求有限集合的子集及其个数．

2．简易逻辑是一个新增内容，据其内容的特点，在高考中应一般在选择题、填空题中出现，如果在解答题中出现，则只会是中低档题．

3．集合、简易逻辑知识，作为一种数学工具，在函数、方程、不等式、排列组合及曲线与方程等方面都有广泛的运用，高考题中常以上面内容为载体，以集合的语言为表现形式，结合简易逻辑知识考查学生的数学思想、数学方法和数学能力，题型常以解答题的形式出现．