1. B．　 2.A　　 3.D　 4.B　 5.A　 6.A　　 7.C　　 8. A　　 9.D　 10.D

22．数列的各项均为正数，为其前项和，对于任意，总有成等差数列．

(1)求数列的通项公式；　

(2)设数列的前项和为，且，求证：对任意实数是常数，和任意正整数，总有

(3)正数数列中，求数列中的最大项．

天津一中2010届高三第五次月考

数学试卷(理)

第I卷

班级　　　　 　　　　姓名　　　　　　 　成绩　　　　　　

_

21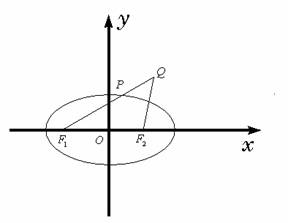．已知椭圆的两个焦点是与，点是椭圆外的动点，满足 。点是线段与该椭圆的交点，点在线段上，并且满足。

(1)设为点的横坐标，证明；

(2)求点的轨迹的方程；

(3)试问：在点的轨迹上，是否存在点，

使的面积为？若存在，求

的正切值；若不存在，请说明理由．

20．已知函数在上为增函数，且，

(1)求的值；

(2)若在上为单调函数，求的取值范围；

(3)设，若在上至少存在一个，使得成立，求的取值范围。

19.　 如图1，在直角梯形中, ,

　 把△沿对角线折起后如图2所示(点记为点), 点在平面上的正投影 落在线段上,　 连接.

　 (1) 求直线与平面所成的角的大小;

(2)　　 求二面角的大小的余弦值.

　　　　　　 图1　　　　　　　　　　　　　　　　　　　　　　 图2

18． 某单位为绿化环境，移栽了甲、乙两种大树各2株．设甲、乙两种大树移栽的成活率分别为和，且各株大树是否成活互不影响．求移栽的4株大树中：

(1)两种大树各成活1株的概率；

(2)成活的株数的分布列与期望．　　

17.已知向量，设函数。

　 (1)求的最小正周期与单调递减区间

　 (2)在中，、、分别是角、、的对边，若的面积为，求的值。

16.已知曲线：，给出以下结论：

①垂直于轴的直线与曲线只有一个交点

②直线()与曲线最多有三个交点

③曲线关于直线对称

④若，为曲线上任意两点，则有

写出正确结论的序号　　　　　　　　 ．

15.编号为的五个小球放在如图所示的五个盒子里,要求每个盒子只能放一个小球,且不能放1,2号,必须放在与相邻的盒子中,则不同的放法有___________种．

14．如果关于x的不等式的解集不是空集，则实数　　　　 的取值范围是　　　　 ．