16、下列说法中不正确的是(B)

A、 共价化合物中也可能含离子键

B、 非金属之间形成的化合物一定是共价化合物

C、 含共价键的化合物不一定是化合物

D、含离子键的化合物一定是离子化合物

15、离子键与共价键的比较

[练习]

[讨论]1、组成原子的粒子有哪些？它们怎样构成原子？

[板书]

2、讨论完成下表：

[板书]1.构成原子及原子核各粒子的概念及相互之间的关系：

(1)原子序数=核电荷数=质子数=核外电子数(中性原子或分子)

(2)核电荷数=质子数=核外电子总数+所带电荷数(原子、分子或离子)

(3)质量数(A)=质子数(Z)+ 中子数(N)。

(4)质量数(A)=该原子相对原子质量的近似整数值。

[归纳]在短周期元素中，许多元素的相对原子质量大约是原子序数的2倍。

[练习]3、某三价阳离子，具有28个电子，质量数为70，核内中子数是

A、28　　　　　 B、31　　　　　 C、39　　　　　 D、42

[例题]4、已知元素X、Y的核电荷数分别是a和b，它们的离子X^m+和Y^n-的核外电子排布相同，则　　　　　　 .

[例题]5、核内中子数为N的R²⁺，质量数为A，则它的ng氧化物中所含质子的物质的量是 　　　　　　　　

[板书]2.核素与同位素，元素的原子量等概念的理解及有关的判断

[例题]6、¹₁H、²₁H、³₁H、H⁺、H₂是(　 )

A.氢的五种同位素　　　 B.五种氢元素　　　 C.氢元素的五种不同粒子　　 D.五种核素

[例题]7、H、D、T分别可以得到　 种不同的氢分子，其化学式和相对分子质量为　　　　　　　　　　　　　　　　　　　　　　　　　 。

[例题]8、有关3517Cl^-粒子，回答下列问题：

(1)　　　 含质子数 　17 ；中子数 18　 ；电子数　 18 　；质量数 35　 。

(2)　　　 该粒子的结构示意图　 (略)　　 ：电子式　 (略) 。

(3)　　　 它与3517Cl、3717Cl之间的关系是 它与是3517Cl同种原子；与3717Cl互为同位素。；

(4)　　　 它与3517Cl的半径大小的关系是 前者大于后者　 .

(5)　　　 已知Cl元素的相对原子质量为35.5，可知原子在自然界的原子质量分数之比为　 3：1 。

[例题]9、设某元素某原子核内的质子数为m，中子数为n，则下述论断正确的是(　 )

A．不能由此确定该元素的相对原子质量

B．这种元素的相对原于质量为m+n

C．若碳原于质量为Wg，此原子的质量为(m+n)Wg；

D．核内中子的总质量小于质子的总质量.

[例题]10、已知，某元素的一种核素的n个原子的质量为Wg，其摩尔质量为M g/mol；则氯元素的一种核素³⁵Cl的一个原子的质量是　　　　 。

[过渡]元素的性质与元素原子的核外电子排布密切相关。因此，了解元素原子核外电子排布的规律是学习化学必须的。

[归纳]原子核外电子排布的一般规律有那些？

[板书]3.核外电子排布规律及结构示意图：

[练习]11、分层排布规律：“一低四不超”的内容是　　　　 ，　　　　　 ，

　　　　　　　　　　　　　　　　　　　　　　　　　　　 。

[例题]12、下列说法或符号中，正确的是：①原子的电子云图中，小黑点的疏密表示电子数的多少；②N的原子结构示意图为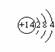；③任何元素的原子都由质子、中子和核外电子构成的；④金属元素的电子数一般少于4个；⑤具有相质子数的粒子属于同一种元素；⑥氘原子结构示意图为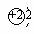；⑦某A原子核内质子数与中子数相等，则元素的相对原子质量是质子数的2倍。(　　 )

A.只有①②④⑦　　 B.只有④⑦　　　　　 C.全部正确　　　　　 D.全部错误

[练习]13、某元素原子的核外电子数是电子层数的5倍，其质子数是最外层电子数的3倍，该元素的原子结构示意图是。

[讲解]由于元素原子的最外层上的电子数与元素的化学性质密切相关，所以为了简便起见，我们引入了电子式的概念。原子、离子的都可以用结构简图和电子式来表示。电子式还可以用于表示化合物的形成过程。

[过渡]原子在参加化学反应时，都有使自己的最外层电子形成稳定结构的倾向，原子和原子相遇发生反应时，必形成化学键。

[板书]二、化学键

[讨论]14、原子和原子通常通过什么方式使自己趋向于稳定结构呢？形成怎样的化学键？

22． 解：(1)由已知，对于任意，总有　 ①成立

　　　　　　　　　　　　　　　　 所以　 ②…………(1分)

①-②得，

均为正数，

数列是公差为1的等差数列…………(3分)

又时，，解得

…………(5分)

(2)证明：对任意实数是常数，和任意正整数，总有

，…………(6分)

　　　　　　　　　　 …………(9分)

(3)由已知

易得

猜想时，是递减数列…………(10分)

令

则，当时，则，

在内，为单调递减函数，…………(12分)

由知

时，是递减数列，即是递减数列， …………(13分)

又数列中的最大项为．…………(14分)

21．解：(1)设，由点在椭圆上，得

　…………(2分)

由，知，

所以…………(4分)

(2)设点

当时，点在轨迹上；

当且时，由得

又

所以为线段的中点。…………(6分)

在中，…………(7分)

所以

综上所述，点的轨迹的方程是…………(8分)

(3)曲线上存在点，使的充要条件是…………(10分)

由①得由②得，

所以，当时，存在点，使

当时，不存在点，使…………(12分)

当时，，

由

又

得。…………(14分)

20．解：(1)由题意：在上恒成立，即，

在上恒成立，只需sin…………(4分)

(2) 由(1),得f(x)-g(x)=mx-,,由于f(x)-g(x)在其定义域内为单调函数，则在上恒成立，即在上恒成立，故，综上，m的取值范围是　　　　　　　　　　　　　　　　 …………(8分)

(3)构造函数F(x)=f(x)-g(x)-h(x),,

当由得，，所以在上不存在一个，使得；　　　　　　　　　　　　　 …………(10分)

当m>0时，，因为，所以在上恒成立，故F(x)在上单调递增，，故m的取值范围是…………(12分)

19. (1) 解:在图4中,

　　　 ∵

　　 　∴,　 , .

　　 ∵,

∴△为等边三角形.　　　　　　　　　　　　　　

∴.　　　　　　 …2分

　　 在图5中,

　　 ∵点为点在平面上的正投影,

∴平面.

∵平面,

∴.

∵,　　　　　　　　　　　 　　　　　　　　　　　　　

∴.

∵平面, 平面,

∴平面.

∴为直线与平面所成的角.　　 …4分

在Rt△中, ,

∴.　　

∵,

∴.

∴直线与平面所成的角为.　　　　 …6分　　　　　　

(2) 解:取的中点, 连接,.

∵ ,

∴ .

∵平面,平面,

∴.

∵平面, 平面,

∴平面.

∵平面,

∴.

∴为二面角的平面角.　　　　　 　　　　　　　　　　　　…8分

在Rt△中,,

∴,.

在Rt△中,.

在Rt△中，.

∴二面角的大小的余弦值为.　　　　　　　　　　　　　　　 …12分

方法二:

　解:在图4中,

　　　 ∵

　　 　∴,　 , .

　　 ∵,

∴△为等边三角形.　　　　　　　　　　　　　　

∴.　　　　　　 …2分

在图5中,

　∵点为点在平面上的射影,　　　　　　　　　　　　　　 图4

∴平面.

∵平面,

∴.

∵,　　　　　　　　　　　　　　　　　　　　　　　

∴.

∵平面, 平面,

∴平面.　　　　　　　　　　　　　 …4分

连接,

在Rt△和Rt△中,,

∴Rt△Rt△.

∴.

∴.

∴.

在Rt△中，.

∴.

在Rt△中，.　　　　　　　　　　　　　　 　…6分

以点为原点,所在直线为轴,与平行的直线为轴,所在直线为轴,建立空　

间直角坐标系,则,,,,

.

∴,,,.　　

(1)∵,

　 ∴.

　 ∴ 直线与平面所成的角为.　　　　　　　　　　　　　　　　　　 …9分　　　　　　

(2) 设平面的法向量为n,

　 由　 得

　 令, 得,.

　 ∴n为平面的一个法向量.　　　　　　　　　　　　　　

　 ∵为平面的一个法向量,

　∴.

　 ∵二面角的平面角为锐角,

　 ∴二面角的平面角的余弦值为.　　　　　　 …12分　

18.解 设表示甲种大树成活k株，k＝0，1，2

表示乙种大树成活l株，l＝0，1，2

则，独立. 由独立重复试验中事件发生的概率公式有

　　, 　.

　据此算得

　,　 　, …………(2分)

　.　　　

　　,　 　, …………(4分)

　.

　(Ⅰ) 所求概率为

　…………(5分)

.

　(Ⅱ) 解法一：

的所有可能值为0，1，2，3，4，且　　

　　,

　　,

　= ,

　　.

　　.

综上知有分布列

	0	1	2	3	4
P	1/36	1/6	13/36	1/3	1/9

　　　　　　　　　　　　…………(10分)

从而，的期望为

(株)…………(12分)

解法二：

分布列的求法同上

令分别表示甲乙两种树成活的株数，则

故有　　　

从而知

17.解：(Ⅰ)，

　　　　　．．．．．．．．．．．．．．．．．．．．3分

　…………………………4分

令　

的单调区间为,k∈Z　　．．．．．．．．．．．．．．．6分

(Ⅱ)由得　　　　

　　　　．．．．．．．．．．．．．．．．．．．7分

又为的内角　　　　　

　　　　．．．．．．．．．．．．．．．．．．9分

　　　　．．．．．．．．．．．．．10分

　　　．．．．．．．．．．．12分

11. 39．　　 12.．　　 13．4　　 14．　　 15．30　　 16．③