
2.计算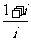 的结果是( )
的结果是( )
A.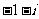 B.
B.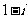 C.
C. D.
D.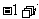
1. 已知函数f(x)=ax2+c,且 =2,则a的值( )
=2,则a的值( )
A.1
B.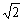 C.-1
D. 0
C.-1
D. 0
17.(本题满分12分)
证明:假设三个方程中都没有两个相异实根,…………2分
则Δ1=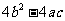 ≤0,Δ2=
≤0,Δ2= ≤0,Δ3=
≤0,Δ3=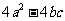 ≤0. ………6分
≤0. ………6分
相加有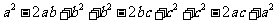 ≤0,……9分
≤0,……9分
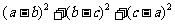 ≤0. ①…………10分
≤0. ①…………10分
由题意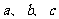 互不相等,∴①式不能成立.
互不相等,∴①式不能成立.
∴假设不成立,即三个方程中至少有一个方程有两个相异实根. ………12分
18解:(Ⅰ)解:当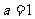 时,
时,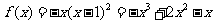 ,得
,得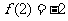 ,且
,且
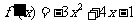 ,
,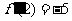
所以,曲线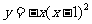 在点
在点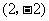 处的切线方程是
处的切线方程是 ,整理得
,整理得
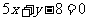 .……4分
.……4分
(Ⅱ)解: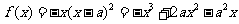
 .令
.令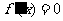 ,解得
,解得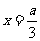 或
或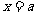 .
.
由于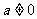 ,以下分两种情况讨论.
,以下分两种情况讨论.
(1)若 ,当
,当 变化时,
变化时,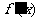 的正负如下表:
的正负如下表:

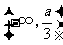
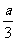
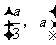
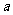
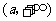
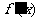
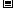
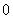

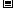
因此,函数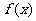 在
在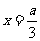 处取得极小值
处取得极小值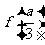 ,且
,且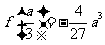 ;函数
;函数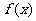 在
在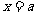 处取得极大值
处取得极大值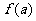 ,且
,且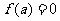 .
.
(2)若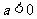 ,当
,当 变化时,
变化时,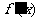 的正负如下表:
的正负如下表:



因此,函数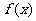 在
在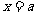 处取得极小值
处取得极小值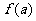 ,且
,且
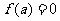 ;函数
;函数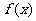 在
在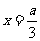 处取得极大值
处取得极大值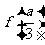 ,且
,且
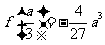 .……10分
.……10分
(Ⅲ)证明:由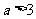 ,得
,得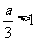 ,当
,当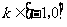 时,
时,
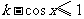 ,
,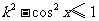 .
.
由(Ⅱ)知,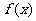 在
在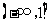 上是减函数,要使
上是减函数,要使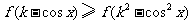 ,
,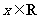
只要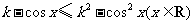
即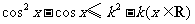 ①
①
设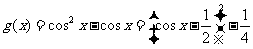 ,则函数
,则函数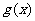 在
在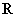 上的最大值为
上的最大值为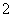 .
.
要使①式恒成立,必须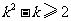 ,即
,即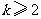 或
或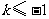 .
.
所以,在区间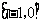 上存在
上存在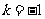 ,使得
,使得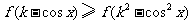 对任意的
对任意的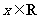 恒成立.…14分
恒成立.…14分
19解:(Ⅰ)设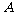 、
、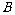 两项技术指标达标的概率分别为
两项技术指标达标的概率分别为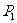 、
、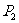 .
.
由题意得: ,解得:
,解得: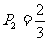 .……3分
.……3分
∴ 一个零件经过检测为合格品的概率 .…5分
.…5分
(Ⅱ)任意抽出5个零件进行检查,其中至多3个零件是合格品的概率为:
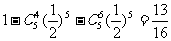 . ……9分
. ……9分
(Ⅲ)依题意知  -
-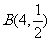 ,…10分
,…10分
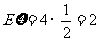 ,
,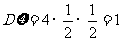 .………14分
.………14分


17.解:(1)随机变量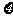 可取的值为
可取的值为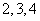 .………1分
.………1分
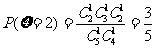 ………3分
………3分
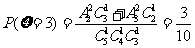 ;…6分
;…6分
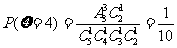 ………9分
………9分
 |
2 |
3 |
4 |
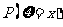 |
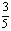 |
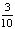 |
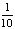 |
得随机变量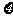 的概率分布律为:
的概率分布律为:
………10分
(2)随机变量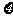 的数学期望为:
的数学期望为: ; ……12分
; ……12分
随机变量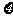 的方差为:
的方差为: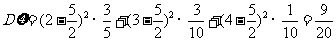 ……14分
……14分
15.解:由于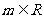 ,复数
,复数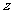 可表示为
可表示为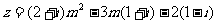
=
(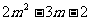 )+ (
)+ (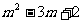 )i
3分
)i
3分
(1)
当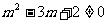 即
即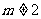 且
且 时,
时,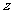 为虚数。 6分
为虚数。 6分
(2)
当 即
即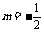 时,
时,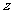 为纯虚数。 9分
为纯虚数。 9分
(3) 当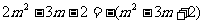 即
即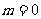 或
或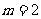 时,
时,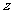 为复平面内第二、四象限角平分线上的点对应的复数。 。12分
为复平面内第二、四象限角平分线上的点对应的复数。 。12分
14.3
13.答案: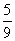 。解析:设“第一次摸到红球”为事件A,“第二次摸到红球”为事件B,则
。解析:设“第一次摸到红球”为事件A,“第二次摸到红球”为事件B,则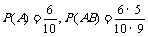 ,∴
,∴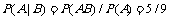 。
。
11。答案: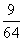 .解析:
.解析: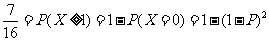 ,解得
,解得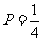 ,故
,故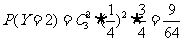 。12。1/12
。12。1/12
9.1或8 10. 1或-1
19.(14分)某工厂在试验阶段大量生产一种零件.这种零件有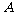 、
、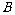 两项技术指标需要检测,设各项技术指标达标与否互不影响.若
两项技术指标需要检测,设各项技术指标达标与否互不影响.若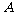 项技术指标达标的概率为
项技术指标达标的概率为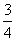 ,有且仅有一项技术指标达标的概率为
,有且仅有一项技术指标达标的概率为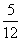 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品.
(Ⅰ)求一个零件经过检测为合格品的概率;
(Ⅱ)任意依次抽出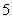 个零件进行检测,求其中至多
个零件进行检测,求其中至多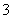 个零件是合格品的概率;
个零件是合格品的概率;
(Ⅲ)任意依次抽取该种零件 个,设
个,设 表示其中合格品的个数,求
表示其中合格品的个数,求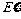 与
与 .
.
CCDA BCCD
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com