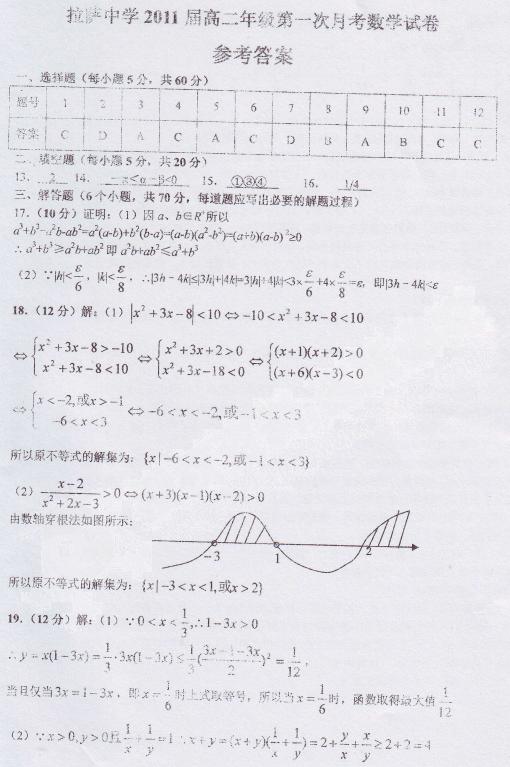
3．如图9－3－18所示，电阻为R，其他电阻均可忽略，ef是一电阻可不计的水平放置的导体棒，质量为m，棒的两端分别与ab、cd保持良好接触，又能沿框架无摩擦下滑，整个装置放在与框架垂直的匀强磁场中，当导体棒ef从静止下滑经一段时间后闭合开关S，则S闭合后(　)

A．导体棒ef的加速度可能大于g

B．导体棒ef的加速度一定小于g

C．导体棒ef最终速度随S闭合时刻的不同而不同

D．导体棒ef的机械能与回路内产生的电能之和一定守恒

解析：开关闭合前，导体棒只受重力而加速下滑．闭合开关时有一定的初速度v₀，若此时F_安>mg，则F_安－mg＝ma.若F_安<mg，则mg－F_安＝ma，F_安不确定，A正确，B错误；无论闭合开关时初速度多大，导体棒最终的安培力和重力平衡，故C错误．再根据能量守恒定律，D正确．

答案：AD

2．如图9－3－17所示，一个小矩形线圈从高处自由落下，进入较小的有界匀强磁场，线圈平面和磁场保持垂直．设线圈下边刚进入磁场到上边刚进入磁场为A过程；线圈全部进入磁场内运动为B过程；线圈下边刚出磁场到上边刚出磁场为C过程，则(　)

A．在A过程中，线圈一定做加速运动

B．在B过程中，线圈机械能不变，并做匀加速运动

C．在A和C过程中，线圈内电流方向相同

D．在A和C过程中，通过线圈某截面的电量相同

解析：由于线圈从高处落下的高度未知，所以进入磁场时的初速度也不知，故进入磁场时，线圈在安培力和重力的作用下可能加速，也可能匀速或减速．B过程中，线圈内不产生感应电流，只受重力作用，所以做匀加速运动，且机械能守恒．由楞次定律知，A、C过程中电流方向相反，A过程为逆时针，C过程为顺时针．由公式q＝t＝·Δt＝，A和C过程线圈磁通量的变化量相同，故通过线圈某截面的电量相同．故正确选项为B、D.

答案：BD

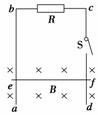
图9－3－18

1．如图9－3－16所示，两个相邻的匀强磁场，宽度均为L，方向垂直纸面向外，磁感应强度大小分别为B、2B.边长为L的正方形线框从位置甲匀速穿过两个磁场到位置乙，规定感应电流逆时针方向为正，则感应电流i随时间t变化的图象是(　)

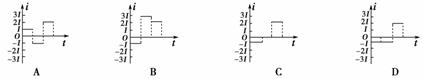
答案：D

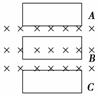
图9－3－17

4．如图9－3－15所示，在距离水平地面h＝0.8 m的虚线的上方，有一个方向垂直于纸面水平向内的匀强磁场，正方形线框abcd的边长l＝0.2 m，质量m＝0.1 kg，电阻R＝0.08 Ω.一条不可伸长的轻绳绕过轻滑轮，一端连线框，另一端连一质量M＝0.2 kg的物体A.开始时线框的cd在地面上，各段绳都处于伸直状态，从如图所示的位置由静止释放物体A，一段时间后线框进入磁场运动，已知线框的ab边刚进入磁场时线框恰好做匀速运动．当线框的cd边进入磁场时物体A恰好落地，同时将轻绳剪断，线框继续上升一段时间后开始下落，最后落至地面．整个过程线框没有转动，线框平面始终处于纸面内，g取10 m/s².求：

(1)匀强磁场的磁感应强度B?

(2)线框从开始运动到最高点，用了多长时间？

(3)线框落地时的速度多大？

解析：(1)设线框到达磁场边界时速度大小为v，由机械能守恒定律可得：

Mg(h－l)＝mg(h－l)+(M+m)v²①

代入数据解得：v＝2 m/s②

线框的ab边刚进入磁场时，感应电流：I＝③

线框恰好做匀速运动，有：Mg＝mg+IBl④

代入数据解得：B＝1 T．⑤

(2)设线框进入磁场之前运动时间为t₁，有：h－l＝vt₁⑥

代入数据解得：t₁＝0.6 s⑦

线框进入磁场过程做匀速运动，所用时间：t₂＝＝0.1 s⑧

此后轻绳拉力消失，线框做竖直上抛运动，到最高点时所用时间：t₃＝＝0.2 s⑨

线框从开始运动到最高点，所用时间：t＝t₁+t₂+t₃＝0.9 s．⑩

(3)线框从最高点下落至磁场边界时速度大小不变，线框所受安培力大小也不变，即

IBl＝(M－m)g＝mg⑪

因此，线框穿出磁场过程还是做匀速运动，离开磁场后做竖直下抛运动．

由机械能守恒定律可得：mv＝mv²+mg(h－l)⑫

代入数据解得线框落地时的速度：v_t＝4 m/s.⑬

答案：(1)1 T　(2)0.9 s　(3)4 m/s

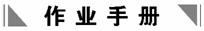
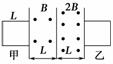
图9－3－16

3．如图9－3－14所示，半径为a的圆环电阻不计，放置在垂直于纸面向里，磁感应强度为B的匀强磁场中，环内有一导体棒电阻为r，可以绕环匀速转动．将电阻R，开关S连接在环和棒的O端，将电容器极板水平放置，并联在R和开关S两端，如图9－3－14所示．

(1)开关S断开，极板间有一带正电q，质量为m的粒子恰好静止，试判断OM的转动方向和角速度的大小．

(2)当S闭合时，该带电粒子以g的加速度向下运动，则R是r的几倍？

解析：(1)由于粒子带正电，故电容器上极板为负极，根据右手定则，OM应绕O点逆时针方向转动．

粒子受力平衡：mg＝q，E＝Ba²ω.当S断开时，U＝E，解得ω＝.

(2)当S闭合时，根据牛顿第二定律mg－q＝m·g，U′＝·R，解得＝3.

答案：(1)OM应绕O点逆时针转动　(2)3

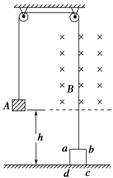
图9－3－15

2．如图9－3－13所示，在水平桌面上放置两条相距l的平行粗糙且无限长的金属导轨ab与cd，阻值为R的电阻与导轨的a、c端相连．金属滑杆MN垂直于导轨并可在导轨上滑动，且与导轨始终接触良好．整个装置放于匀强磁场中，磁场的方向竖直向上，磁感应强度的大小为B.滑杆与导轨电阻不计，滑杆的中点系一不可伸长的轻绳，绳绕过固定在桌边的光滑轻滑轮后，与一质量为m的物块相连，拉滑杆的绳处于水平拉直状态．现若从静止开始释放物块，用I表示稳定后回路中的感应电流，g表示重力加速度，设滑杆在运动中所受的摩擦阻力恒为F_f，则在物块下落过程中(　)

A．物体的最终速度为　 　　B．物体的最终速度为

C．稳定后物体重力的功率为I²R　 　　D．物体重力的最大功率可能大于

解析：由题意分析可知，从静止释放物块，它将带动金属滑杆MN一起运动，当它们稳定时最终将以某一速度做匀速运动而处于平衡状态，设MN的最终速度为v，对MN列平衡方程：+F_f＝mg，∴v＝，所以A项正确；又从能量守恒定律角度进行分析，物块的重力的功率转化为因克服安培力做功而产生的电热功率和克服摩擦力做功产生热功率，所以有：I²R+F_fv＝mgv，所以，v＝，所以B项正确，C项错误；物块重力的最大功率为P_m＝mgv＝mg，所以D错误．

答案：AB

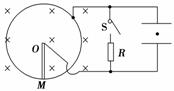
图9－3－14

1.(2010·扬州模拟)如图9-3-12甲所示，光滑导轨水平放置在与水平方向夹角60?°?斜向下的匀强磁场中，匀强磁场的磁感应强度B随时间的变化规律如图乙所示(规定斜向下为正方向)，导体棒ab垂直导轨放置，除电阻R的阻值外，其余电阻不计，导体棒ab在水平外力作用下始终处于静止状态.规定a→b的方向为电流的正方向，水平向右的方向为外力的正方向，则在0~t时间内，能正确反映流过导体棒ab的电流i和导体棒ab所受水平外力F随时间t变化的图象是

解析：由楞次定律可判定回路中的电流始终为b→a方向，由法拉第电磁感应定律可判定回路电流大小恒定，故A、B两项错；由F_安=BIL可得F安随B的变化而变化，在0~t₀时间内，F_安方向向右，故外力F与F_安等值反向，方向向左为负值；在t?₀~t时间内，F安方向改变，故外力F方向也改变为正值，综上所述，?D项正确.　

答案：D

图9－3－13

22．(本小题满分12分)

已知>>，且()=(－)+(－)+(－)

(1)求证：方程()= 0总有两个正实根；

(2)求不等式()≤0的解集；

(3)求使()>(－)(－1)对于3≤2+恒成立的的取值范围。

21．(本小题满分12分)

某单位建造一间地面面积为12米²的背面靠墙的长方体小房子。由于地理位置的限制，房子的侧面长度x不得超过5米，房屋正面造价为400元/米²，房屋侧面造价为150元/米²，屋顶和地面造价费用合计5800元，如果墙高3米，且不计房屋背面的费用，

(1)把房屋总造价y表示成x的函数，并写出该函数的定义域；

(2)当侧面的长度x为多少时，总造价最低？最低总造价是多少？

20．(本小题满分12分)如果关于x的不等式ax²+bx+c<0的解集是{x|x<1，或x>2}，求关于x的不等式c x²-bx+a <0的解集。