
8.若向量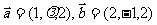 ,且
,且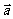 与
与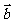 的夹角余弦为
的夹角余弦为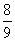 ,则
,则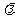 等于_________________.
等于_________________.
7.在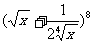 的展开式中有理项的项数共有 项。
的展开式中有理项的项数共有 项。
6.已知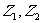 是复平面上两个定点,点
是复平面上两个定点,点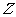 在线段
在线段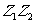 的垂直平分线上,根据复数的几何意义,则点
的垂直平分线上,根据复数的几何意义,则点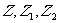 所对应的复数
所对应的复数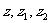 满足的关系式为
。
满足的关系式为
。
5.若复数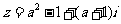 (
(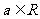 )是纯虚数,则
)是纯虚数,则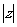 = ___.
= ___.
4.若 ,w*w^w.k&s#5@则
,w*w^w.k&s#5@则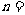 ____________
____________
3.已知点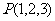 ,
,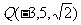 ,它们在面
,它们在面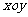 内的射影分别是
内的射影分别是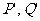 ,则
,则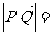 。
。
2. 复数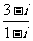 等于 。
等于 。
1. “因为四边形ABCD是菱形,所以四边形ABCD的对角线互相垂直”,补充以上推理的大前提是 。
21.本题主要考察函数、导数、不等式的证明等基础知识,同事考察综合运用数学知识进行推理论证的能力和分类讨论的思想。(满分14分)
解:(Ⅰ)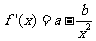 ,则有
,则有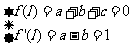 ,解得
,解得 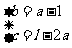
(Ⅱ)由(Ⅰ)知,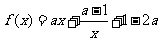 ,
,
令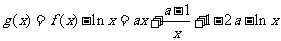 ,
,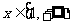
则 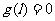 ,
,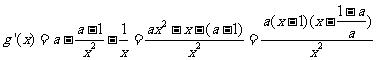
(i)当
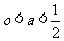 ,
,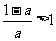
若 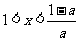 ,则
,则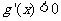 ,
,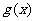 是减函数,所以
是减函数,所以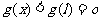
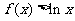 ,故
,故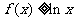 在
在 上恒不成立。
上恒不成立。
(ii)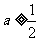 时,
时,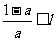
若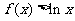 ,故当
,故当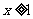 时,
时,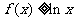
综上所述,所求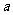 的取值范围为
的取值范围为
20.本小题主要考察等差数列、等比数列等基础知识以及反证法,同时考查推理论证能力。
(满分13分)
解:(Ⅰ)由题意可知,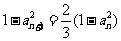
令 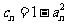 ,则
,则 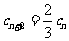
又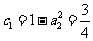 ,则数列
,则数列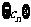 是首项为
是首项为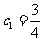 ,公比为
,公比为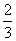 的等比数列,即
的等比数列,即
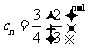 ,故
,故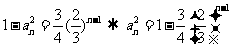 ,
,
又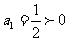 ,
,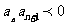
故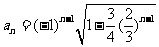
(Ⅲ)解法一:由(Ⅱ)知:当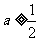 时,有
时,有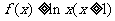 。
。
令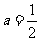 ,有
,有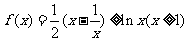
当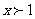 时,
时,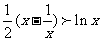 。
。
令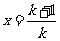 ,有
,有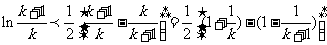
即 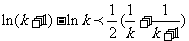 ,
,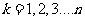
将上述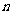 个不等式一次相加得
个不等式一次相加得
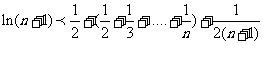
整理得
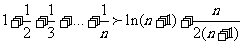
解法二:用数学归纳法证明
(1)
当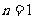 时,左边
时,左边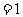 ,右边
,右边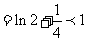 ,不等式成立
,不等式成立
(2)
假设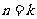 时, 不等式成立, 就是
时, 不等式成立, 就是
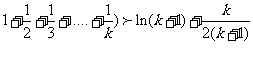
那么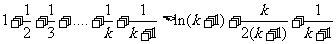
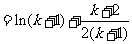
由(Ⅱ)知:当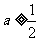 时,有
时,有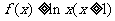
令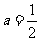 ,有
,有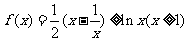
令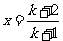 ,得:
,得: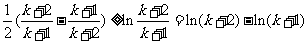
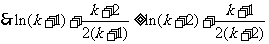
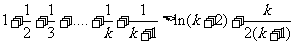
就是说, 当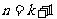 时,不等式也成立。
时,不等式也成立。
根据(1)和(2),可知不等式对任何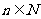 都成立。
都成立。

(Ⅱ)用反证法证明
假设数列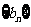 存在三项
存在三项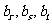
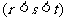 按某种顺序成等差数列,由于数列
按某种顺序成等差数列,由于数列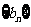 是首项为
是首项为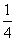 ,公比为
,公比为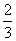 的等比数列,于是有
的等比数列,于是有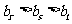 ,则只有可能有
,则只有可能有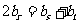 成立
成立
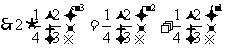
两边同乘3t t2t-r,化简得3t-r+22t-r=2*2t-r3t-s
由于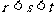 ,所以上式左边为奇数,右边为偶数,故上上式不可能成立,导致矛盾。故数列
,所以上式左边为奇数,右边为偶数,故上上式不可能成立,导致矛盾。故数列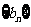 中任意三项不可能成等差数列。
中任意三项不可能成等差数列。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com