
4. 胚胎发育的早期有一段时间是在透明带中进行的,这一时期称为卵裂期。其特点是
A.细胞进行有丝分裂,所有细胞均具有全能性
B.每个细胞体积有所减小,胚胎的总体积增加
C.胚胎有机物总量增加,细胞DNA总量不断减少
D.所有细胞的相对表面积减小,核物质(质量)与质物质比值增大
3.有关PCR技术的说法,不正确的是
A.PCR是一项在生物体外复制特定的DNA片段的核酸合成技术
B.PCR技术的原理是DNA双链复制
C.利用PCR技术获取目的基因的前提是要有一段已知目的基因的核苷酸序列
D.PCR扩增中必须有解旋酶才能解开双链DNA
2.一般来说,动物细胞体外培养需要满足以下条件:
①无毒的环境 ②无菌的环境 ③合成培养基需加血清、血浆 ④温度与动物体温相近
⑤需要O2,不需要CO2 ⑥需要CO2调节培养液pH
A.①②③④⑤⑥ B.①②③④ C.①③④⑤⑥ D.①②③④⑥
1.将目的基因导入微生物细胞的最常用方法是
A.感受态细胞法 B.显微注射法 C.基因枪法 D.农杆菌转化法
21.(2010湖南文数)(本小题满分13分)
已知函数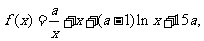 其中a<0,且a≠-1.
其中a<0,且a≠-1.
(Ⅰ)讨论函数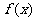 的单调性;
的单调性;
(Ⅱ)设函数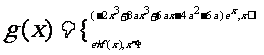 (e是自然数的底数)。是否存在a,使
(e是自然数的底数)。是否存在a,使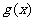 在[a,-a]上为减函数?若存在,求a的取值范围;若不存在,请说明理由。
在[a,-a]上为减函数?若存在,求a的取值范围;若不存在,请说明理由。



(2010浙江理数) (22)(本题满分14分)已知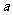 是给定的实常数,设函数
是给定的实常数,设函数 ,
,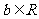 ,
,
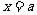 是
是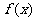 的一个极大值点.
的一个极大值点.
(Ⅰ)求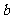 的取值范围;
的取值范围;
(Ⅱ)设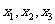 是
是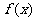 的3个极值点,问是否存在实数
的3个极值点,问是否存在实数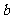 ,可找到
,可找到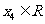 ,使得
,使得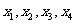 的某种排列
的某种排列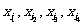 (其中
(其中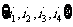 =
=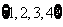 )依次成等差数列?若存在,求所有的
)依次成等差数列?若存在,求所有的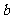 及相应的
及相应的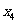 ;若不存在,说明理由.
;若不存在,说明理由.
解析:本题主要考查函数极值的概念、导数运算法则、导数应用及等差数列等基础知识,同时考查推理论证能力、分类讨论等综合解题能力和创新意识。
(Ⅰ)解:f’(x)=ex(x-a)
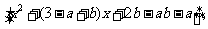
令
于是,假设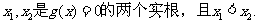
(1) 当x1=a 或x2=a时,则x=a不是f(x)的极值点,此时不合题意。
(2) 当x1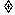 a且x2
a且x2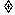 a时,由于x=a是f(x)的极大值点,故x1<a<x2.
a时,由于x=a是f(x)的极大值点,故x1<a<x2.
即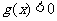
即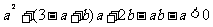
所以b<-a
所以b的取值范围是(-∞,-a)
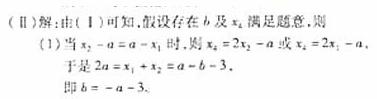
此时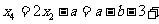

或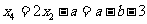

(2)当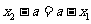 时,则
时,则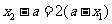 或
或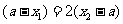

于是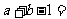
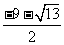

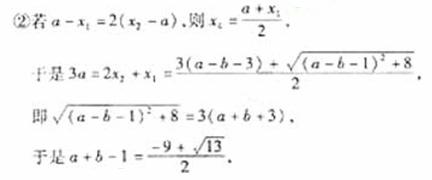
此时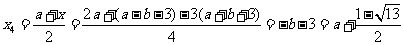
综上所述,存在b满足题意,
当b=-a-3时,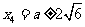
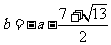 时,
时,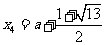
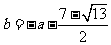 时,
时,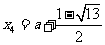
(2010全国卷2理数)(22)(本小题满分12分)
设函数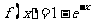 .
.
(Ⅰ)证明:当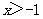 时,
时,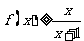 ;
;
(Ⅱ)设当 时,
时,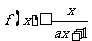 ,求a的取值范围.
,求a的取值范围.
[命题意图]本题主要考查导数的应用和利用导数证明不等式,考查考生综合运用知识的能力及分类讨论的思想,考查考生的计算能力及分析问题、解决问题的能力.
22.(2010上海文数)(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分5分,第3小题满分8分。
若实数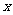 、
、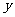 、
、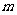 满足
满足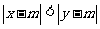 ,则称
,则称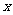 比
比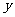 接近
接近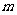 .
.
(1)若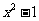 比3接近0,求
比3接近0,求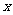 的取值范围;
的取值范围;
(2)对任意两个不相等的正数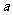 、
、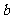 ,证明:
,证明: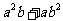 比
比 接近
接近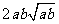 ;
;
(3)已知函数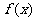 的定义域
的定义域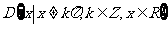 .任取
.任取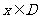 ,
,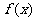 等于
等于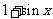 和
和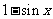 中接近0的那个值.写出函数
中接近0的那个值.写出函数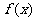 的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明).
的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明).
解析:(1) xÎ(-2,2);
(2) 对任意两个不相等的正数a、b,有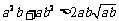 ,
,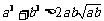 ,
因为
,
因为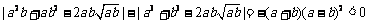 ,
所以
,
所以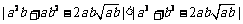 ,即a2b+ab2比a3+b3接近
,即a2b+ab2比a3+b3接近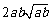 ;
(3)
;
(3) 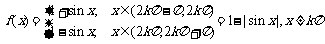 ,kÎZ,
f(x)是偶函数,f(x)是周期函数,最小正周期T=p,函数f(x)的最小值为0,
函数f(x)在区间
,kÎZ,
f(x)是偶函数,f(x)是周期函数,最小正周期T=p,函数f(x)的最小值为0,
函数f(x)在区间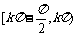 单调递增,在区间
单调递增,在区间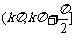 单调递减,kÎZ.
单调递减,kÎZ.
6. (2010江苏卷)14、将边长为1m正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记 ,则S的最小值是____▲____。
,则S的最小值是____▲____。
[解析] 考查函数中的建模应用,等价转化思想。一题多解。
设剪成的小 正三角形的边长为
正三角形的边长为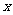 ,
, 则:
则: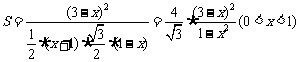
(方法一)利用导数求函数最小值。
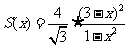 ,
,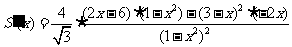

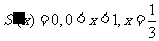 ,
,
当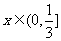 时,
时,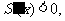 递减;当
递减;当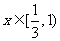 时,
时,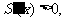 递增;
递增;
故当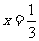 时,S的最小值是
时,S的最小值是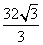 。
。
(方法二)利用函数的方法求最小值。
令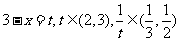 ,则:
,则: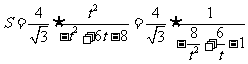
故当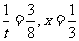 时,S的最小值是
时,S的最小值是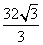 。
。
2010年高考数学试题分类汇编--函数
5. (2010江苏卷)11、已知函数 ,则满足不等式
,则满足不等式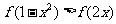 的x的
的x的 范围是__▲___。
范围是__▲___。
[解析] 考查分段函数的单调性。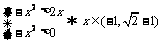
4. (2010江苏卷)5、设函数f(x)=x(ex+ ae-x)(x
ae-x)(x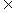 R)是偶函数,则实数
R)是偶函数,则实数 a=_______▲_________
a=_______▲_________
[解析]考查函数的奇偶性的知识。g(x)=ex+ae-x为奇函数,由g(0)=0,得a=-1。
3. (2010福建理数)15.已知定义域为 的函数
的函数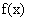 满足:①对任意
满足:①对任意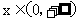 ,恒有
,恒有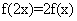 成立;当
成立;当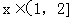 时,
时,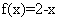 。给出如下结论:
。给出如下结论:
①对任意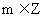 ,有
,有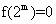 ;②函数
;②函数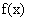 的值域为
的值域为 ;③存在
;③存在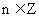 ,使
,使 得
得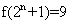 ;④“函数
;④“函数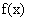 在区间
在区间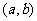 上单调递减”的充要条件是
“存在
上单调递减”的充要条件是
“存在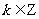 ,使得
,使得
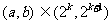 ”。
”。
其 中所有正确结论的序号是
。
中所有正确结论的序号是
。
[答案]①②④
[解析]对①,因为 ,所以
,所以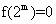 ,故①正确;经分析,容易得出②④也正确。
,故①正确;经分析,容易得出②④也正确。
[命题意图]本题考查函数的性质与充要条件,熟练基础知识是解答好本题的关键。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com