
17.(1)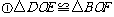 ; 证明:∵四边形
; 证明:∵四边形 是平行四边形
∴
是平行四边形
∴ ∴
∴ 又∵
又∵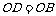 ∴
∴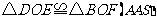
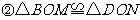 证明:∵四边形
证明:∵四边形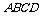 是平行四边形∴
是平行四边形∴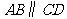
∴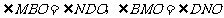 又∵
又∵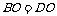 ∴
∴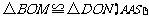
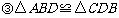 ;证明:∵四边形
;证明:∵四边形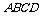 是平行四边形
∴
是平行四边形
∴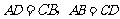
又∵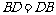 ∴
∴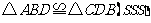
(2)绕点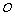 旋转
旋转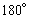 后得到或以点
后得到或以点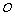 为中心作对称变换得到.
为中心作对称变换得到.
16.解:原式=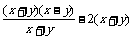 =
=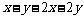 =
=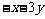 当
当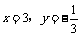 时
时
原式=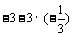
15. 解:(1)由图象可知,函数
解:(1)由图象可知,函数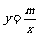 (
(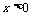 )的图象经过点
)的图象经过点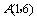 ,可得
,可得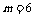 .
.
设直线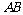 的解析式为
的解析式为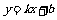 .
.
∵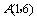 ,
,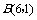 两点在函数
两点在函数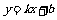 的图象上,
的图象上,
∴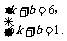 解得
解得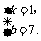
∴直线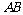 的解析式为
的解析式为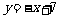 .
.
(2)3.
14.解: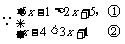 由①得
由①得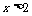 ,由②得,
,由②得,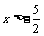
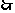 原不等式组的解集为
原不等式组的解集为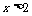
13.解:(1)文文的作法较好 (或彬彬的较好)
(2)在△ABC中,AB=AC,AD⊥BC,∴AD是△ABC的中线, 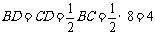 .
.
在Rt△ABD中,AB=10,BD=4,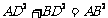 ,
,
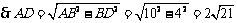 .
.
12.解:(1)20;(2)3600;(3)1250.(注:每小题答对给2分)
11.解: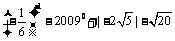
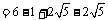
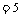 .
.
(三)
20.为了整治环境卫生,某地区需要一种消毒药水3250瓶,药业公司接到通知后马上采购两种专用包装箱,将药水包装后送往该地区.已知一个大包装箱价格为5元,可装药水10瓶;一个小包装箱价格为3元,可以装药水5瓶.该公司采购的大小包装箱共用了1700元,刚好能装完所需药水.
(1)求该药业公司采购的大小包装箱各是多少个?
(2)药业公司准备派A、B两种型号的车共10辆运送该批药水,已知A型车每辆最多可同时装运30大箱和10小箱药水;B型车每辆最多可同时装运20大箱和40小箱消毒药水,要求每辆车都必须同时装运大小包装箱的药水,求出一次性运完这批药水的所有车型安排方案.
(3)如果A型车比B型车省油,采用哪个方案最好?
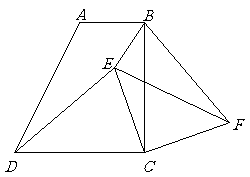
21.如图,在梯形 中,
中, ,
,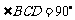 ,
,
且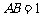 ,
,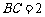 ,
,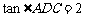 .
.
(1)求证: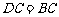 ;
;
(2)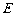 是梯形内一点,
是梯形内一点,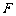 是梯形外一点,且
是梯形外一点,且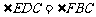 ,
,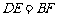 ,试判断
,试判断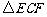 的形状,并证明你的结论;
的形状,并证明你的结论;
(3)在(2)的条件下,当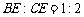 ,
,
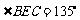 时,求
时,求 的值.
的值.
22.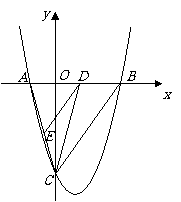 已知:抛物线
已知:抛物线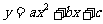 与x轴交于A、B两点,与y轴交于点C. 其中点A在x轴的负半轴上,点C在y轴的负半轴上,线段OA、OC的长(OA<OC)是方程
与x轴交于A、B两点,与y轴交于点C. 其中点A在x轴的负半轴上,点C在y轴的负半轴上,线段OA、OC的长(OA<OC)是方程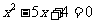 的两个根,且抛物线的对称轴是直线
的两个根,且抛物线的对称轴是直线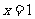 .
.
(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)若点D是线段AB上的一个动点(与点A、B不重合),过点D作DE∥BC交AC于点E,连结CD,设BD的长为m,△CDE的面积为S,求S与m的函数关系式,并写出自变量m的取值范围.S是否存在最大值?若存在,求出最大值并求此时D点坐标;若不存在,请说明理由.
19. 如图,在梯形ABCD中,AB∥CD,BD⊥AD,BC=CD,∠A=60°,CD=2cm.
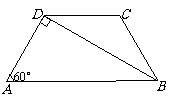 (1)求∠CBD的度数;
(1)求∠CBD的度数;
(2)求下底AB的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com