
(16)△ABC的面积是30,内角A,B,C,所对边长分别为a,b,c,cosA=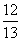 .
.
(1)求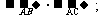
(2)若c-b= 1,求a的值.
1,求a的值.
(17)椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率 .
.
(1)求椭圆E的方程;
(2)求∠F1AF2的角平分线所在直线的方程.

18、(本小题满分13分)
某市20104月1日-4月30日对空气 污染指数的检测数据如下(主要污染物为可吸入颗粒物):
污染指数的检测数据如下(主要污染物为可吸入颗粒物):
61,76,70,56,81,91,92,91,75 ,81,88,67,101,103,95,91,
,81,88,67,101,103,95,91,
77,86,81,83,82,82,64,79,86,85,75,71,49,45,
(Ⅰ) 完成频率分布表;
(Ⅱ)作出频率分布直方图;
(Ⅲ)根据国家标准,污 染指数在0~50之间时
染指数在0~50之间时 ,空气质量为优:在51~100之间时,为良;在101~150之间时,为轻微污染;在151~200之间时,为轻度污染。
,空气质量为优:在51~100之间时,为良;在101~150之间时,为轻微污染;在151~200之间时,为轻度污染。
请你依据所给数据和上述标准,对 该市的空气质量给出一个简短评价.
该市的空气质量给出一个简短评价.
(19) (本小题满分13分)
如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,E F∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,
F∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,
(Ⅰ)求证:FH∥平面EDB;
(Ⅱ)求证:AC⊥平面EDB;

(Ⅲ)求四面体B-DEF的体积;
(20)(本小题满分12分)
设函数f(x)= sinx-cosx+x+1, 0﹤x﹤2∏,求函数f(x)的单调区间与极值.
sinx-cosx+x+1, 0﹤x﹤2∏,求函数f(x)的单调区间与极值.
(21)(本小题满分13分)
设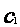 ,
, ...,
..., ,…是坐标平面上的一列圆,它们的圆心都在x轴的正半轴上,且都与直线y=
,…是坐标平面上的一列圆,它们的圆心都在x轴的正半轴上,且都与直线y= x相切,对每一个正整数n,圆
x相切,对每一个正整数n,圆 都与圆
都与圆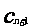 相互外切,以
相互外切,以 表示
表示 的半径,已知
的半径,已知 为递增数列.
为递增数列.
(Ⅰ)证明: 为等比数列;
为等比数列;
(Ⅱ)设 =1,求数列
=1,求数列 的前n项和.
的前n项和. 
(11)命题“存在x∈R,使得x2+2x+5=0”的否定是
(12)抛物线y2=8x的焦点坐标是
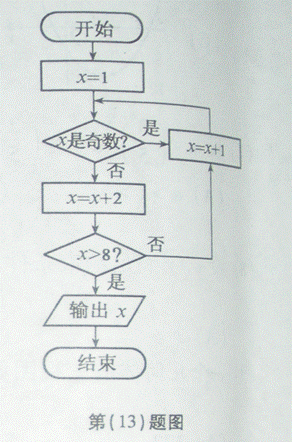
(13)如图所示,程序框图(算法流程图)的输出值x=
(14)某地有居民100000户,其中普通家庭99 000户,高收入家庭1 000户.从普通家庭中以简单随机抽样方式抽取990户,从高收入家庭中以简单随机抽样方式抽取l00户进行调查,发现共有120户家庭拥有3套或3套以上住房,其中普通家庭50户,高收人家庭70户.依据这些数据并结合所掌握的统计知识,你认为该地拥有3套或3套以上住房的家庭所占比例的合理估计是 .
(15)若a>0 ,b>0,a+b=2,则下列不等式对一切满足条件的a.
,b>0,a+b=2,则下列不等式对一切满足条件的a.
b恒成立的是 (写出所有正确命题的编号).
①ab≤1; ②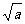 +
+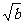 ≤
≤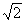 ; ③a2+b2≥2;
; ③a2+b2≥2;
④a3+b3≥3; 
(1)若A=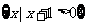 ,B=
,B= ,则
,则 =
=
(A)(-1,+∞) (B)(-∞,3) (C)(-1,3) (D)(1,3)
(2)已知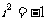 ,则i(
,则i( )=
)=
(A)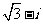 (B)
(B)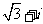 (C)
(C)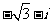 (D)
(D)
(3)设向量 ,
, ,则下列结论中正确的是
,则下列结论中正确的是
(A)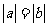 (B)
(B)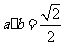
(C)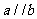
 (D)
(D) 与
与 垂直
垂直
(4)过 点(1,0)且与直线x-2y-2=0平行的直线方程是
点(1,0)且与直线x-2y-2=0平行的直线方程是
(A)x-2y-1=0 (B)x-2y+1=0
(C)2x+y-2=0 (D)x+2y-1=0
(5)设数列{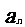 }的前n项和
}的前n项和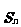 =
=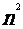 ,则
,则 的值为
的值为
(A) 15 (B) 16 (C) 49 (D)64
(6)设abc>0,二次函数f(x)=a +bx+c的图像可能是
+bx+c的图像可能是

(7)设a= ,b=
,b= ,c=
,c=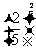 ,则a,b,c的大小关系是
,则a,b,c的大小关系是
(A)a>c>b (B)a>b>c (C)c>a>b (D)b>c>a
(8)设x,y满足约束条件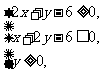 则目标
则目标 函数z=x+y的最大值是
函数z=x+y的最大值是
(A)3 (B) 4 (C) 6 (D)8
(9)一个几何体的三视图如图,该几何体的表面积是
(A)372 (C)292
(B)360 (D)280


(10)甲从正方形四个顶点中任意选择两个顶点连成直线,一页从该正方形四个顶点中任意选择连个顶点连成直线,则所得的两条直线相互垂直的概率是
(A)
 (A)
(A) (A)
(A)
 (A)
(A)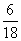
数 学(文科)(安徽卷)
第Ⅱ卷(非选择题共100分)
请用0 5毫米黑色墨水签字笔在答题卡上作答,在试题卷上大体无效。
25.解:(1)依题意,得
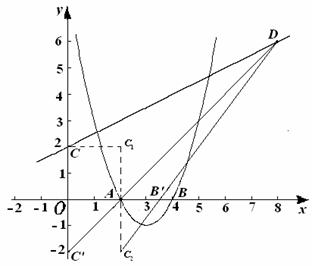

解得 
∴抛物线的解析式是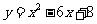 .
.
…………………… 2分
(2)依题意,得 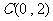 ,
, .
.
………………………… 3分
作点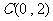 关于x轴的对称点
关于x轴的对称点 ,求直线
,求直线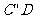 的解析式为
的解析式为 ,直线
,直线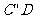 与x轴的交点即为P点.因此,P点坐标为
与x轴的交点即为P点.因此,P点坐标为 .
.
………………………………………………………………………… 4分
(3)左右平移抛物线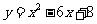 ,因为线段A′B′=2和CD=
,因为线段A′B′=2和CD=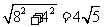 均是定值,所以要使四边形A′B′DC的周长最小,只要使A′C+B′D的值最小; …………………………………………………………………… 5分
均是定值,所以要使四边形A′B′DC的周长最小,只要使A′C+B′D的值最小; …………………………………………………………………… 5分
因为A′B′=2,因此将点C向右平移2个单位得C1(2,2),
作点C1关于x轴的对称点C2,C2点的坐标为 (2,-2),
设直线C2D的解析式为 ,
,
将点C2 (2,-2)、D(8,6)代入解析式,得

解得 
∴直线C2D的解析式为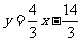 .
.
∴直线C2D与x轴的交点即为B′点,可求B′( ,0),因此A′(
,0),因此A′(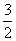 ,0).
,0).
所以当四边形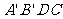 的周长最小时,
的周长最小时,
抛物线的解析式为 ,即
,即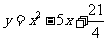 . …… 6分
. …… 6分
∵A′C+B′D=C2D= . ………………………………… 7分
. ………………………………… 7分
∴四边形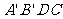 的周长最小值为
的周长最小值为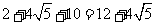 . …… 8分
. …… 8分
24.(1)解:等腰梯形(或矩形,或正方形). ……………………………… 1分
(2)证法一:取AC的中点H,连接HE、HF.
∵点E为BC的中点,
∴EH为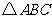 的中位线.
的中位线.
∴ ∥
∥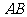 ,且
,且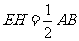 . ………………………… 2分
. ………………………… 2分
 同理
同理 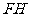 ∥
∥ ,且
,且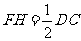 . …………………… 3分
. …………………… 3分
∵AB=AC,DC=AC,
∴AB=DC.
∴EH=FH.
∴ . ………………… 4分
. ………………… 4分
∵ ∥
∥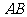 ,
,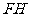 ∥
∥ ,
,
∴ ,
, .
.
∴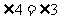 .
.
∵ ,
, ,
,
∴ . ………………………………………… 5分
. ………………………………………… 5分
∴四边形AGEC是等邻角四边形. …………………………… 6分
证法二:连接AE.
设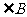 的度数为x,
的度数为x,
∵AB=AC,CD=CA,
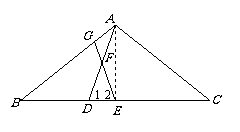 ∴
∴ ,
, .………………… 2分
.………………… 2分
∵F是AD的中点,
∴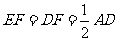 .…… 3分
.…… 3分
∴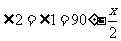 .
.
∴ .
.
 . …………………… 4分
. …………………… 4分
∴ . ………………………………………… 5分
. ………………………………………… 5分
∴四边形AGEC是等邻角四边形. …………………………… 6分
(3)存在等邻角四边形,为四边形AGHC. ……………………… 7分
23.解:(1)旋转后的图象解析式为
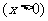 . ……………………… 1分
. ……………………… 1分
(2)由旋转可得 (4,-1)、
(4,-1)、 (1,-4). ………………………… 3分
(1,-4). ………………………… 3分
(3)依题意,可知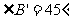 .若
.若 为直角三角形,则
为直角三角形,则 同时也是等腰三角形,因此,只需求使
同时也是等腰三角形,因此,只需求使 为直角三角形的
为直角三角形的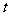 值.
值.
分两种情况讨论:
①当 是直角,
是直角,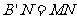 时,如图1,
时,如图1,
∵AB′=8,B′A′==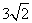 ,AM=B′N=MN=t,
,AM=B′N=MN=t,
 ∴B′M=8-t,
∴B′M=8-t,
∵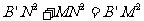 ,
,
∴ . ………… 4分
. ………… 4分
解得 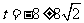 (舍去负值),
(舍去负值),
∴ . ……………… 5分
. ……………… 5分
②当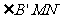 是直角,
是直角, 时,
时,
如图2,
∵AB′=8,B′A′==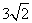 ,AM=B′N=t,
,AM=B′N=t,
 ∴B′M=MN=8-t,
∴B′M=MN=8-t,
∵ ,
,
∴ ,
,
解得  .
.
∵ ,
,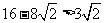 ,
,
∴此时t值不存在. …………… 6分
(此类情况不计算,通过画图说明t值不存在也可以)
综上所述,当 时,
时, 为等腰直角三角形. ……………… 7分
为等腰直角三角形. ……………… 7分
22. 解:(1)
解:(1) 的面积
的面积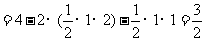 . …………… 1分
. …………… 1分
(2)如图,平移后的三角形为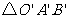 .
.
(画图正确给1分,累计2分)
平移的距离 .
.
…………………………………… 3分
平移过程中 所扫过的面积为
所扫过的面积为
四边形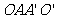 与
与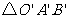 的面积和,
的面积和,
即 .
.
…………………………………… 4分
21.(1)证明:∵AB是⊙O的直径,
∴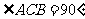 . ………………………………………… 1分
. ………………………………………… 1分
∴ .
.
∵ ,
,
∴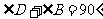 .
.
∴ . ………………………………………… 2分
. ………………………………………… 2分
∴AD为⊙O的切线. ……………………………………… 3分
(2)解:∵ ,
, ,
,
在Rt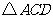 中,
中,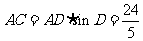 ,
,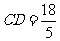 .
.
在Rt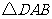 中,
中,
 .
.
∴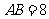 ,
,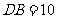 . ……………………………………… 4分
. ……………………………………… 4分
∵AE平分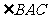 ,
, ,
,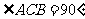 ,
,
∴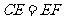 .
.
设 ,则
,则 ,
,
∵ ,
, ,
,
∴ ∽
∽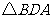 .
.
∴ ,即
,即 .
.
∴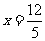 .
.
即CE的长为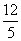 . ……………………………………………… 5分
. ……………………………………………… 5分
20.




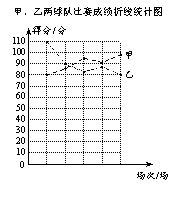 解:(1)如图;………………………… 1分
解:(1)如图;………………………… 1分
(2) =90(分);………………… 2分
=90(分);………………… 2分
(3)甲队成绩的极差是18分,
乙队成绩的极差是30分;…………… 4分
(4)从平均分看,两队的平均分相同,实力大体相当;
从折线的走势看,甲队比赛成绩呈上升趋势,
而乙队比赛成绩呈下降趋势;从获胜场数看,
甲队胜三场,乙队胜两场,甲队成绩较好;
从极差看,甲队比赛成绩比乙队比赛成绩波动小,甲队成绩较稳定.
综上,选派甲队参赛更能取得好成绩.…………………………………… 6分
19.解:分别过点A、D作 ,
,

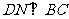 ,垂足分别为M、N.
,垂足分别为M、N.
可得四边形AMND是矩形.
∴MN=AD=6. ……………… 1分
∵AB=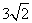 ,
,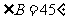 ,
,
∴ , ………… 2分
, ………… 2分
∴DN=AM=3. …………………………………………………………… 3分
∵ ,
,
∴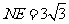 . …………………………………………………………… 4分
. …………………………………………………………… 4分
∴BE=BM+MN+NE= . ………………………… 5分
. ………………………… 5分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com