
21.(本小题满分13分)
数列 中,
中,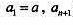 是函数
是函数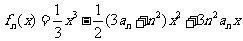 的极小值点
的极小值点
(Ⅰ)当a=0时,求通项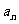 ;
;
(Ⅱ)是否存在a,使数列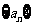 是等比数列?若存在,求a的取值范围;若不存在,请说明理由。
是等比数列?若存在,求a的取值范围;若不存在,请说明理由。
20.(本小题满分13分)
已知函数 对任意的
对任意的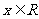 ,恒有
,恒有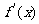

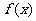 。
。
(Ⅰ)证明:当 时,
时,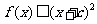 ;
;
(Ⅱ)若对满足题设条件的任意b,c,不等式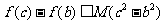 恒成立,求M的最小值。
恒成立,求M的最小值。
19.(本小题满分13分)
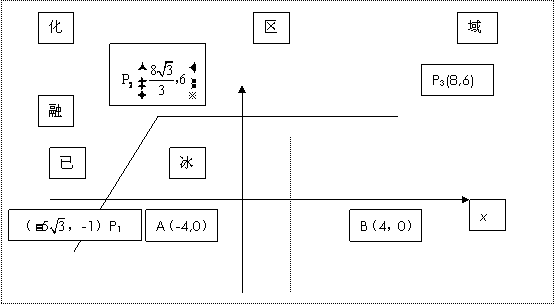
为了考察冰川的融化状况,一支科考队在某冰川上相距8km的A,B两点各建一个考察基地。视冰川面为平面形,以过A,B两点的直线为x轴,线段AB的的垂直平分线为y轴建立平面直角坐标系(图6)在直线x=2的右侧,考察范围为到点B的距离不超过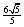 km区域;在直线x=2的左侧,考察范围为到A,B两点的距离之和不超过
km区域;在直线x=2的左侧,考察范围为到A,B两点的距离之和不超过 km区域。
km区域。
(Ⅰ)求考察区域边界曲线的方程;
(Ⅱ)如图6所示,设线段P1P2,P2P3是冰川的部分边界线(不考虑其他边界线),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍,求冰川边界线移动到考察区域所需的最短时间。

18.(本小题满分12分)
如图5所示,在正方体 E是棱
E是棱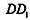 的中点。
的中点。
(Ⅰ)求直线BE的平面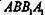 所成的角的正弦值;
所成的角的正弦值;
(II)在棱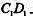 上是否存在一点F,使
上是否存在一点F,使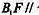 平面
平面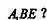 证明你的结论。
证明你的结论。
17.(本小题满分12分)
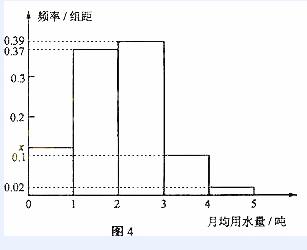
图4是某城市通过抽样得到的居民某年的月均用水量(单位:吨)的频率分布直方图
(Ⅰ)求直方图中x的值
(II)若将频率视为概率,从这个城市随机抽取3位居民(看作有放回的抽样),求月均用水量在3至4吨的居民数X的分布列和数学期望。
16.(本小题满分12分)
已知函数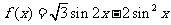 .
.
(Ⅰ)求函数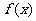 的最大值;
的最大值;
(II)求函数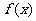 的零点的集合。
的零点的集合。
15.若数列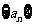 满足:对任意的
满足:对任意的 ,只有有限个正整数
,只有有限个正整数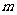 使得
使得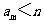 成立,记这样的
成立,记这样的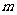 的个数为
的个数为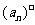 ,则得到一个新数列
,则得到一个新数列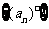 .例如,若数列
.例如,若数列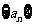 是
是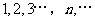 ,则数列
,则数列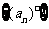 是
是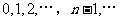 .已知对任意的
.已知对任意的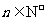 ,
,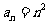 ,则
,则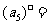 ,
,
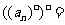
 .
.
14.过抛物线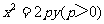 的焦点作斜率为1的
的焦点作斜率为1的 直线与该抛物线交于
直线与该抛物线交于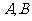 两点,
两点,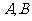 在
在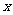 轴上的正射影分别为
轴上的正射影分别为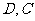 .若梯形
.若梯形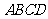
 的面积为
的面积为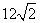 ,则
,则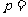 .
.
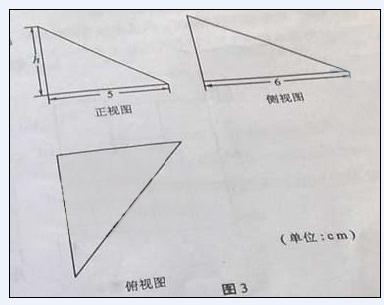
13.图3中的三个直角三角形是 一个体积为20
一个体积为20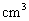 的几何体的三视图,则
的几何体的三视图,则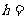
 .
.
12.图2是求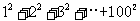 的值的程序框图,则正整数
的值的程序框图,则正整数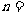 .
.
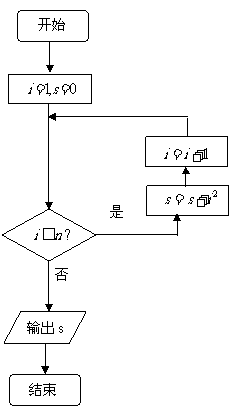

图2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com