
4.已知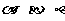 是三个不同的平面,命题“
是三个不同的平面,命题“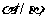 且
且 ”是正确的。如果把
”是正确的。如果把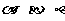 中的任意两个换成直线,在所得的命题中,真命题有
中的任意两个换成直线,在所得的命题中,真命题有
A.0个 B.1个 C.2个 D.3个
3.已知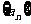 为等差数列,
为等差数列, ,
,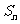 是等差数列
是等差数列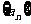
的前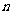 项和 ,则使得
项和 ,则使得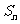 到达最大值的
到达最大值的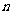 是
是
A. B.
B.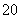 C.
C.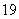 D.
D.
2.设 的反函数为
的反函数为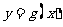 ,若
,若 ,则
,则 等于
等于
A. B.
B.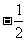 C.2 D.
C.2 D.
1.集合 ,则
,则 ( )
( )
A. B.
B.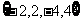 C.
C. D.
D. 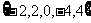
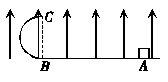
13.(14分)如图所示,竖直放置的半圆形绝缘轨道的半径为R,下端与光滑绝缘水平面平滑连接,整个装置处于方向竖直向上的场强大小为E的匀强电场中.现有一质量为m、带电荷量为+q的物块(可视为质点)从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好通过最高点C,已知E<.
(1)试计算物块在运动过程中克服摩擦力做的功.
(2)证明物块离开轨道落回水平面的水平距离与场强大小E无关,且为一常量.
解析:(1)物块恰能通过圆弧最高点C,即圆弧轨道此时与物块间无弹力作用,物块受到的重力和电场力提供向心力,则:
mg-Eq=m
物块在由A运动到C的过程中,设物块克服摩擦力做的功为Wf,根据动能定理知:
Eq·2R-Wf-mg·2R=mv-mv
解得:Wf=mv+(Eq-mg)R.
(2)物块离开半圆形轨道后做类平抛运动,设水平位移为s,则s=vCt
2R=(g-)·t2
联立解得:s=2R
因此,物块离开轨道落回水平面的水平距离与场强大小E无关,恒为2R.
答案:(1)mv+(Eq-mg)R
(2)物块离开轨道落回水平面的水平距离与场强大小E无关,恒为2R
12.(13分)弹射器是航母制造中的关键技术之一,重型喷气式战斗机在水平跑道上需要滑行450 m以上才能达到起飞速度,而即使当今最大的“尼米兹”级航空母舰甲板的长度也不过300余米,依靠弹射器是重型战斗机在航母上起飞的必不可少的环节.
已知美军F-14战斗机重3.0×107 kg,在地面跑道上靠自身发动机提供动力需滑行450 m才能到达250 km/h的起飞速度,而这种战斗机在“尼米兹”号航母上,在蒸汽弹射器和自身发动机动力的共同作用下,可在45 m内将速度加到 250 km/h.若F-14战斗机加速度滑行时,发动机动力和飞机受到的阻力都恒定,则“尼米兹”号上蒸汽弹射器使一架F-14 战斗机起飞至少要做多少功?
解析:设F-14战斗机自身发动机的牵引力为F,受到的阻力为f,在水平地面跑道上起飞时,由动能定理有:
 (F-f)·s1=mv2-0
(F-f)·s1=mv2-0
在“尼米兹”号航母甲板上起飞时,有:
W+Fs2-fs2=mv2
解得:弹射器至少需做的功W=6.5×1010 J.
答案:6.5×1010 J
11.(13分)一质量为500 t的机车,以恒定功率375 kW由静止出发,经过5 min速度达到最大值54 km/h,设机车所受阻力f恒定不变,取g=10 m/s2,试求:
(1)机车受到的阻力f的大小.
(2)机车在这5 min内行驶的路程.
解析:研究对象为机车.首先分析物理过程:机车以恒定功率P0由静止出发→速度v增加→牵引力F减小(P0=Fv)→合力减小(F合=F-f)→加速度减小(a=)→速度继续增加→直至合力减小为0,加速度a=0,速度达到最大.

可见机车在这5 min内做的是加速度减小、速度不断增大的变速运动.当机车的速度达到最大时,P0=Fvmax,此时F=f,机车的受力情况如图所示.
(1)已知P0=375 kW=3.75×105 W
vmax=54 km/h=15 m/s
根据P0=Fvmax时F=f,得:P0=fvmax
机车受到的阻力f== N=2.5×104 N.
(2)机车在这5 min内,牵引力为变力,做正功,阻力做负功,重力、弹力不做功.
根据P0=,牵引力做的功为:WF=P0·t
根据动能定理有:
P0·t-f·s=mv-0
解得:s=
= m
=2250 m.
答案:(1)2.5×104 N (2)2250 m
10.在光滑的水平面上有一静止的物体,现以水平恒力F1推这一物体,作用一段时间后换成相反方向的水平恒力F2推这一物体,当恒力F2作用的时间与恒力F1作用的时间相等时,物体恰好回到原处,此时物体的动能为32 J,则在整个过程中,恒力F1、F2做的功分别为( )
A.16 J、16 J B.8 J、24 J
C.32 J、0 J D.48 J、-16 J
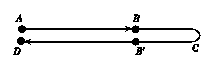
解析:如图所示,设两过程的时间均为t,A到B过程中,物体的加速度大小为a1;B到D过程中,物体的加速度大小为a2.取向右的方向为正方向,设AB=s,可得:
s=a1t2
-s=v0t-a2t2
v0=a1t
解得:a2=3a1
因为F1=ma1,F2=ma2
解得:F2=3F1
又由动能定理得:
W1+W2=ΔEk=32 J
W1=F1·s
W2=F2·s
可得:W1=8 J,W2=24 J.
答案:B
非选择题部分共3小题,共40分.
9.如图所示,物体的质量为1 kg,动滑轮和细绳的质量均不计.现用一竖直向上的拉力F拉动细绳,使物体从静止开始以5 m/s2的加速度匀速上升,则拉力F在1 s末的瞬时功率是(g取10 m/s2)( )
A.150 W B.75 W C.37.5 W D.25 W
解析:设与重物连接的悬绳的拉力为F′,由牛顿第二定律得:
F′-mg=ma
解得:F′=15 N.
方法一 每时刻拉力做功的功率都等于悬绳对重物做功的功率,故P=F′·v=F′·at=75 W.
方法二 由动滑轮的特点知,F=F′,拉力F作用点上升的加速度为10 m/s2,故P=F·v′=×10×1 W=75 W.
答案:B
8.如图所示,一内壁粗糙的环形细圆管位于竖直平面内,环的半径为R(比细管的直径大得多),在圆管中有一个直径与细管内径相同的小球(可视为质点),小球的质量为m.设某一时刻小球通过轨道的最低点时对管壁的压力为6mg,此后小球便做圆周运动,经过半个圆周恰能通过最高点,则在此过程中小球克服摩擦力所做的功是( )
A.3mgR B.2mgR C.mgR D.mgR
解析:设小球在环形管最低点的速度大小为v,由向心力公式得:6mg-mg=m
可得小球在最低点的动能为:
Ek=mv2=mgR
又由题意知,小球到达最高点时速度等于零,设这一过程管壁摩擦力对小球做的功为Wf,由动能定理得:
WG+Wf=0-mv2
即-mg·2R+Wf=-mgR
 解得:Wf=-mgR
解得:Wf=-mgR
即小球克服摩擦力做的功为mgR.
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com