
7.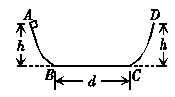 如图所示,ABCD是一个盆式容器,盆内侧壁与盆底BC的连接处都是一段与BC相切的圆弧,BC水平,其长d=0.50 m,盆边缘的高度h=0.30 m.在A处放一个质量为m的小物块并让其由静止开始下滑.已知盆内侧壁是光滑的,而盆底BC面与小物块间的动摩擦因数μ=0.10.小物块在盆内来回滑动,最后停止下来,则小物块停止时的位置到B的距离为( )
如图所示,ABCD是一个盆式容器,盆内侧壁与盆底BC的连接处都是一段与BC相切的圆弧,BC水平,其长d=0.50 m,盆边缘的高度h=0.30 m.在A处放一个质量为m的小物块并让其由静止开始下滑.已知盆内侧壁是光滑的,而盆底BC面与小物块间的动摩擦因数μ=0.10.小物块在盆内来回滑动,最后停止下来,则小物块停止时的位置到B的距离为( )
A.0.50 m B.0.25 m C.0.10 m D.0
解析:对小物块从A点出发到最后停下来的整个过程,由动能定理有:mgh-μmgs=0
所以s==3 m
而d=0.50 m,刚好三个来回,所以最终停在B点.
答案:D
6.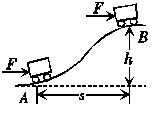 如图所示,质量为 m的小车在水平恒力F的推动下,从山坡底部A处由静止起运动至高为h的坡顶B,获得速度为v,A、B的水平距离为s.下列说法正确的是( )
如图所示,质量为 m的小车在水平恒力F的推动下,从山坡底部A处由静止起运动至高为h的坡顶B,获得速度为v,A、B的水平距离为s.下列说法正确的是( )
A.小车克服重力所做的功是mgh
B.推力对小车做的功是mv2
C.推力对小车做的功是Fs-mgh
D.阻力对小车做的功是mv2+mgh-Fs
解析:重力对小车做的功WG=-mgh,故选项A正确.由功的定义知W推=F·s,由动能定理有W推-mgh+W阻=mv2,故W阻=mv2+mgh-Fs.故选项B、C错误,选项D正确.
答案:AD
5. 据《科技日报》2007年12月23日报道,时速为300公里的“和谐号”动车组是在引进、消化和吸收国外时速200公里动车组技术平台的基础上,由中国自主研发制造的世界上运营速度最高的动车组列车之一.如果列车受到的阻力与其运行速度的二次方成正比,当速度由原来的200
km/h提高到现在的300
km/h后,机车发动机的功率要变为原来的( )
据《科技日报》2007年12月23日报道,时速为300公里的“和谐号”动车组是在引进、消化和吸收国外时速200公里动车组技术平台的基础上,由中国自主研发制造的世界上运营速度最高的动车组列车之一.如果列车受到的阻力与其运行速度的二次方成正比,当速度由原来的200
km/h提高到现在的300
km/h后,机车发动机的功率要变为原来的( )
A.倍 B.()2倍 C.()3倍 D.()4倍
解析:当列车匀速运动时,动力大小等于受到的阻力,故:
机车功率P=F·v=kv2·v
=()3=()3.
答案:C
4.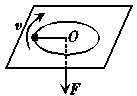 如图所示,质量为m的物体用穿过光滑小孔的细绳牵引,使其在光滑水平面上做匀速圆周运动,拉力为某个值F时,转动半径为R;当拉力逐渐减小到时,物体仍做匀速圆周运动,半径为2R.则此过程中外力对物体所做的功为( )
如图所示,质量为m的物体用穿过光滑小孔的细绳牵引,使其在光滑水平面上做匀速圆周运动,拉力为某个值F时,转动半径为R;当拉力逐渐减小到时,物体仍做匀速圆周运动,半径为2R.则此过程中外力对物体所做的功为( )
A.FR B.-FR C.FR D.0
解析:设物体在前后两种情况下做圆周运动的线速度分别为v1、v2,此过程中外力对物体所做的功为W,由动能定理得:
W=mv-mv
又由题意有:
F=m
F=m
解得:W=-FR.
(注:不能通过W=s=·Rcos π来计算,即≠P)
答案:B
3. 如图所示,滑块以6 m/s的初速度从曲面上的A点滑下,运动到B点(比A点低)时速度仍为 6 m/s.若滑块以5 m/s的初速度仍由A点下滑,则它运动到B点时的速度( )
如图所示,滑块以6 m/s的初速度从曲面上的A点滑下,运动到B点(比A点低)时速度仍为 6 m/s.若滑块以5 m/s的初速度仍由A点下滑,则它运动到B点时的速度( )
A.大于5 m/s B.等于5 m/s
C.小于5 m/s D.无法确定
解析:两次下滑中,滑块做圆周运动时,曲面对滑块的弹力不同,则滑块受到的摩擦力不同,故摩擦力对滑块做的功不同,而重力对滑块做的功相同,故两次动能的变化不同.因第二次速度小一点,滑块做圆周运动时,曲线对它的弹力也小一些,故它受到的摩擦力也随之减小,因此它克服摩擦力做的功也相应地减小,从而小于滑块重力做的功(因为第一次滑块克服摩擦力做的功等于滑块重力做的功),故末速度大于初速度.
答案:A
2.在水平粗糙的地面上,使同一物体由静止开始做匀加速直线运动,第一次是斜向上的拉力F,第二次是斜向下的推力F.两次力的作用线与水平方向的夹角相同,力的大小相同,位移的大小也相同.则在这两次力的作用过程中( )
A.力F对物体做的功相同,合力对物体做的总功也相同
B.力F对物体做的功相同,合力对物体做的总功不相同
C.力F对物体做的功不相同,合力对物体做的总功相同
D.力F对物体做的功不相同,合力对物体做的总功也不相同
解析:两力对物体做的功W=Fscos α相同,合外力做的功:第一次W1=(Fcos α-μmg+μFsin α)s;第二次W2=(Fcos α-μmg-μFsin α)s.
答案:B
1.用力将重物竖直提起,先由静止开始匀加速上升,紧接着匀速上升.如果前后两过程的运动时间相同,不计空气阻力,则( )
A.加速过程中拉力做的功比匀速过程中拉力做的功大
B.匀速过程中拉力做的功比加速过程中拉力做的功大
C.两过程中拉力做的功一样大
D.上述三种情况都有可能
解析:匀加速运动的位移s1=at2,匀速运动的位移s2=at·t=2s1,当匀加速上提时的拉力F=2mg时,两过程拉力做的功相等;当F<2mg时,匀加速过程拉力做的功比匀速上升过程拉力做的功小;当F>2mg时,匀加速过程拉力做的功比匀速上升过程拉力做的功大.
答案:D
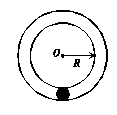
6.某游乐场中有一种“空中飞椅”的游乐设施如图甲所示,其基本装置是将绳子上端固定在转盘上,下端连接座椅,人坐在座椅上随着转盘旋转而在空中飞旋,若将人看成质点,则可简化为如图乙所示的物理模型.其中P为处于水平面内的转盘,可绕竖直转轴OO′转动.设轻绳长l=10 m,人及椅的总质量m=60 kg,转盘不动时人和转轴间的距离d=4 m,转盘慢慢加速运动,经过一段时间转速保持稳定,此时人和转轴间的距离D=10 m,且保持不变,不计空气阻力,绳子不可伸长,取g=10 m/s2.问:
 (1)最后转盘匀速转动时的角速度为多少?
(1)最后转盘匀速转动时的角速度为多少?
(2)转盘从静止启动到稳定这一过程中,绳子对其中一座椅及人做了多少功?
解析:
(1)设最后转盘匀速转动时的角速度为ω,此时人和座椅的受力情况如图丙所示.有:
FTcos θ=mg
FTsin θ=mDω2,其中sin θ= 甲 乙

解得:ω= rad/s.
(2)从转盘启动到匀速转动的过程中飞椅提升的高度为:
h=l-lcos θ=2 m
设这一过程绳对座椅做的功为W,由动能定理得:
W-mgh=m·(ωD)2
解得:W=3450 J. 丙
答案:(1) rad/s (2)3450 J
金典练习十一 功 功率 动能定理
选择题部分共10小题,每小题6分.在每小题给出的四个选项中,有的小题只有一个选项正确,有的小题有多个选项正确.
5. 如图所示,质量为1 kg的物体沿一曲面从A点无初速度滑下,滑至曲面的最低点B时,下滑的高度为5 m,速度为6 m/s,则在下滑过程中,物体克服阻力所做的功为多少?(g取10 m/s2)
如图所示,质量为1 kg的物体沿一曲面从A点无初速度滑下,滑至曲面的最低点B时,下滑的高度为5 m,速度为6 m/s,则在下滑过程中,物体克服阻力所做的功为多少?(g取10 m/s2)
解析:设物体克服阻力所做的功为Wf,由动能定理得:
mgh-Wf=mv2-0
解得:Wf=1×10×5 J-×1×62 J=32 J.
答案:32 J
4. 如图所示,质量为M、长为l的小车静止在光滑的水平面上,质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动.物块和小车之间的摩擦力为f.物块滑到小车的最右端时,小车运动的距离为s.在这个过程中,下列结论错误的是( )
如图所示,质量为M、长为l的小车静止在光滑的水平面上,质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动.物块和小车之间的摩擦力为f.物块滑到小车的最右端时,小车运动的距离为s.在这个过程中,下列结论错误的是( )
A.物块到达小车最右端时具有的动能为(F-f)(l+s)
B.物块到达小车最右端时,小车具有的动能为fs
C.物块克服摩擦力所做的功为f(l+s)
D.物块和小车增加的机械能为Fs
解析:在本题中计算外力对物块和小车做功时都要取大地为参考系,故选项A、B、C正确.
又因为系统机械能的增加等于物块、小车的动能增加之和,即ΔE=(F-f)(l+s)+fs=F(l+s)-fl,选项D错误.
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com