
9.如果用右图表示各种概念之间的关系,下表所示选项中与图示相符的是
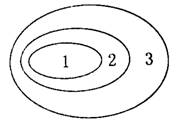
|
选项 |
1 |
2 |
3 |
|
A |
染色体 |
DNA |
基因 |
|
B |
光合作用 |
同化作用 |
新陈代谢 |
|
C |
细胞免疫 |
非特异性免疫 |
特异性免疫 |
|
D |
细菌 |
真菌 |
分解者 |
8.某科研机构利用遥感卫星长期监控一个生态系统的演变,以下三幅示意图是根据不同时期卫星所拍摄的该生态系统照片绘制而成的。图中形状和颜色均相同的点表示同一物种,不 同形状或颜色的点表示不同的物种,点的疏密表示单位面积上种群个体数量的多少。据图所作的结论正确的是

 图一:距今25年
图二:距今l0年
图三:现在
图一:距今25年
图二:距今l0年
图三:现在
A.距今25年时,该生态系统中共有l1个种群
B.距今25年前,该生态系统的稳定性比现在更强
C.近25年来,该生态系统所有生产者合成有机物的总量大于自身分解有机物的总量
D.近25年来,该生态系统种群个体数量不断增加但物种数量不变
7.下面是甲、乙两种物质的结构示意图,图中小圆圈均代表碳原子。这两种物质在氧气中完全燃烧后的产物都是二氧化碳,但它们的物理性质却明显不同,如导电性、硬度等。据此,下列说法错误的是
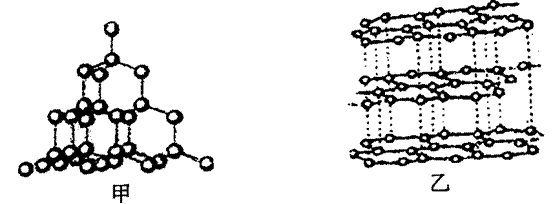
A.甲乙两种物质中的碳原子大小相同
B.甲乙两种物质都是碳单质
C.甲乙两种物质中原子的空间排列方式不同
D.将甲乙两种物质混合后得到的是纯净物
6.有关电和磁的说法正确的是
A..两个着形磁铁靠近时一定会会相互排斥
B.指南针静止时它的北极总是指向地理的南极
C.电磁铁磁性强弱可以用改变电流大小来控制
D.直流电动机转动方向不能由电流方向来控制
5.关于惯性,下列说法正确的足
A..只有不受任何力的物体才有惯性 B.汽车的运动速度越大惯性也越大
C..汽车只有在紧急蒯车时才有惯性 D.物体在任何情况下都具有惯
4.繁殖季节,雄棘鱼腹部颜色由银白色变成红色,并会对侵入其领地的其它雄棘鱼发动攻击性行为。某人为研究引发雄棘鱼攻击性行为的原因,做了如下实验:在雄棘鱼活动的水域中放置了多种颜色的鱼形蜡制模型,并观察和记录雄棘鱼在单位时间内对这些模型进行攻击的次数,实验结果如下表。
|
模型特征 |
攻击频率 |
|
腹部银色 |
低 |
|
腹部红色 |
高 |
|
腹部有红色条纹 |
高 |
根据实验结果所作的推论正确的是:'
A.雄棘鱼的攻击性行为足一种条件反射;
B.有条纹的模型更容易引发雄棘鱼的攻击性行为
C.雄棘鱼的攻击性行为足先天性的,由基因决定
D..腹部有红色的模型更容易发雄棘鱼的攻击性行为
3.下列不属于科学问题的是
A.千岛湖中哪种鱼脂肪含量最低
B.杭州植物园内哪种花卉最美观
C.杭州西溪国家湿地公园内哪几种植物存冬季开花
D.天目山自然保护区内哪种植物自然生长速度最快
2.2007年,我国首次调整饮用水标准。ww新《标准》规定,饮用水的pH在6.5-8.0之间,符合健康标准。w由于受酸雨影响(在我国酸雨中一般含有少量的硫酸),目前我国天然水体大多呈弱酸性。w要使pH低于6. 5的天然水达到饮用水的酸碱度范围,下列处理方法最可行的是
A.加热 B.加入适量纯碱 C.加入适量氯化钡 D.加入适量明矾
1. 下列用品中,由有机合成材料制成的是
A.玻璃杯 B.瓷碗 C.木桌 D.塑料瓶
(18)(本题满分)在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足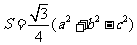 。
。
(Ⅰ)求角C的大小;
(Ⅱ)求 的最大值。
的最大值。
解析本题主要余弦定理、三角形面积公式、三角变换等基础知识,同时考查三角运算求解能力。
(Ⅰ)解:由题意可知
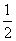 absinC=
absinC=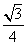 ,2abcosC.
,2abcosC.
所以tanC=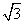 .
.
因为0<C<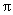 ,
,
所以C=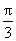 .
.
(Ⅱ)解:由已知sinA+sinB=sinA+sin(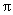 -C-A)=sinA+sin(
-C-A)=sinA+sin(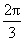 -A)
-A)
=sinA+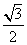 cosA+
cosA+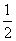 sinA=
sinA=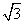 sin(A+
sin(A+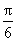 )≤
)≤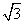 .
.
当△ABC为正三角形时取等号,
所以sinA+sinB的最大值是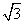 .
.
(19)(本题满分14分)设a1,d为实数,首项为a1,公差为d的等差数列{an}的前n项和为Sn,满足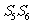 +15=0。
+15=0。
(Ⅰ)若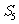 =5,求
=5,求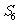 及a1;
及a1;
(Ⅱ)求d的取值范围。
解析:本题主要考查等差数列概念、求和公式等基础知识,同时考查运算求解能力及分析问题解决问题的能力。
(Ⅰ)解:由题意知S6=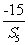 =-3,
=-3,
A6=S6-S5=-8
所以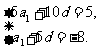
解得a1=7
所以S6= -3,a1=7
(Ⅱ)解:因为S5S6+15=0,
所以(5a1+10d)(6a1+15d)+15=0,
即2a12+9da1+10d2+1=0.
故(4a1+9d)2=d2-8.
所以d2≥8.[
故d的取值范围为d≤-2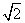 或d≥2
或d≥2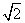 .
.
(20)(本题满分14分)如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°。E为线段AB的中点,将△ADE沿直线DE翻折成△A’DE,使平面A’DE⊥平面BCD,F为线段A’C的中点。
(Ⅰ)求证:BF∥平面A’DE;
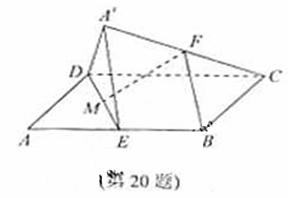 (Ⅱ)设M为线段DE的中点,求直线FM与平面A’DE所成角的余弦值。
(Ⅱ)设M为线段DE的中点,求直线FM与平面A’DE所成角的余弦值。
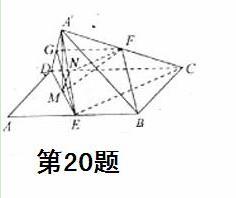 解析:本题主要考查空间线线、线面、面面位置关系,线面角等基础知识,同时考查空间想象能力和推理论证能力。
解析:本题主要考查空间线线、线面、面面位置关系,线面角等基础知识,同时考查空间想象能力和推理论证能力。
(Ⅰ)证明:取A′D的中点G,连结GF,CE,由条件易知
FG∥CD,FG=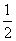 CD.
CD.
BE∥CD,BE=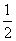 CD.
CD.
所以FG∥BE,FG=BE.
故四边形BEGF为平行四边形,
所以BF∥EG
 因为
因为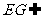 平面
平面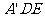 ,BF
,BF 平面
平面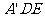
所以 BF//平面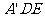
(Ⅱ)解:在平行四边形,ABCD中,设BC=a
则AB=CD=2a, AD=AE=EB=a,
连CE
因为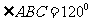
在△BCE中,可得CE=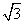 a,
a,
在△ADE中,可得DE=a,
在△CDE中,因为CD2=CE2+DE2,所以CE⊥DE,
在正三角形A′DE中,M为DE中点,所以A′M⊥DE.
由平面A′DE⊥平面BCD,
可知A′M⊥平面BCD,A′M⊥CE.
取A′E的中点N,连线NM、NF,
所以NF⊥DE,NF⊥A′M.
因为DE交A′M于M,
所以NF⊥平面A′DE,
则∠FMN为直线FM与平面A′DE新成角.
在Rt△FMN中,NF=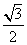 a, MN=
a, MN=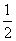 a, FM=a,
a, FM=a,
则cos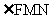 =
=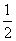 .
.
所以直线FM与平面A′DE所成角的余弦值为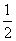 .
.
(21)(本题满分15分)已知函数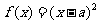 (a-b)
(a-b)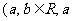 <b)。
<b)。
(I)当a=1,b=2时,求曲线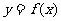 在点(2,
在点(2,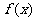 )处的切线方程。
)处的切线方程。
(II)设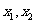 是
是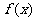 的两个极值点,
的两个极值点,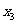 是
是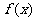 的一个零点,且
的一个零点,且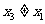 ,
,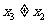
证明:存在实数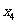 ,使得
,使得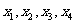 按某种顺序排列后的等差数列,并求
按某种顺序排列后的等差数列,并求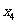
解析:本题主要考查函数的极值概念、导数运算法则、切线方程、导线应用、等差数列等基础知识,同时考查抽象概括、推理论证能力和创新意识。
(Ⅰ)解:当a=1,b=2时,
因为f’(x)=(x-1)(3x-5)
故f’(2)=1
f(2)=0,
所以f(x)在点(2,0)处的切线方程为y=x-2
(Ⅱ)证明:因为f′(x)=3(x-a)(x-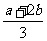 ),
),
由于a<b.
故a<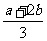 .
.
所以f(x)的两个极值点为x=a,x=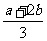 .[
.[
不妨设x1=a,x2=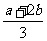 ,
,
因为x3≠x1,x3≠x2,且x3是f(x)的零点,
故x3=b.
又因为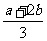 -a=2(b-
-a=2(b-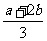 ),
),
x4=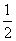 (a+
(a+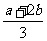 )=
)=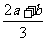 ,
,
所以a,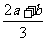 ,
,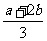 ,b依次成等差数列,
,b依次成等差数列,
所以存在实数x4满足题意,且x4=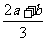 .
.
(22)、(本题满分15分)已知m是非零实数,抛物线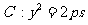 (p>0)
(p>0)
的焦点F在直线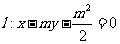 上。
上。
(I)若m=2,求抛物线C的方程
(II)设直线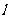 与抛物线C交于A、B,△A
与抛物线C交于A、B,△A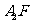 ,△
,△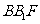 的重心分别为G,H
的重心分别为G,H
求证:对任意非零实数m,抛物线C的准线与x轴的焦点在以线段GH为直径的圆外。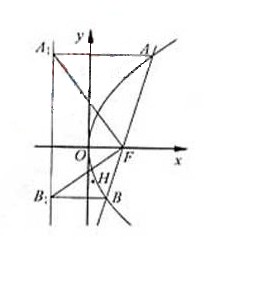
解析:本题主要考查抛物线几何性质,直线与抛物线、点与圆的位置关系等基础知识,同时考查解析几何的基本思想方法和运算求解能力。
(Ⅰ)解:因为焦点F(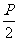 ,0)在直线l上,
,0)在直线l上,
得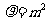
又m=2,故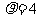
所以抛物线C的方程为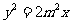
设A(x1,y1) , B(x2,y2)
由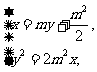 消去x得
消去x得
y2-2m3y-m4=0,
由于m≠0,故 =4m6+4m4>0,
=4m6+4m4>0,
且有y1+y2=2m3,y1y2=-m4,
设M1,M2分别为线段AA1,BB1的中点,
由于2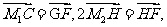
可知G(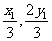 ),H(
),H(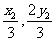 ),
),
所以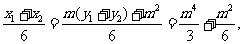
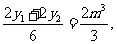
所以GH的中点M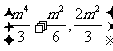 .
.
设R是以线段GH为直径的圆的半径,
则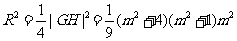
设抛物线的标准线与x轴交点N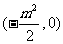 ,
,
则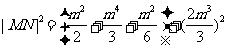
=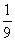 m4(m4+8 m2+4)
m4(m4+8 m2+4)
=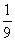 m4[(m2+1)( m2+4)+3m2]
m4[(m2+1)( m2+4)+3m2]
>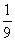 m2 (m2+1)( m2+4)=R2.
m2 (m2+1)( m2+4)=R2.
故N在以线段GH为直径的圆外.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com