
9.(2010年高考陕西卷理科7)若某空间几何体的三视图如图所示,则该几何体的体积是 [ ]
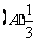



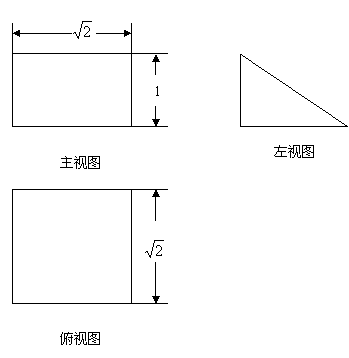

(第7小题图)
[答案]C
[解析]由所给三视图知,对应的几何体为一倒放的直三棱柱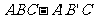 (如下图所示),其高为
(如下图所示),其高为 ,底面
,底面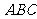 满足:
满足: .
.
故该几何体的体积为 .故选
.故选 .
.
|

8.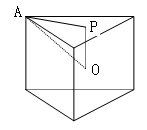 (2010年全国高考宁夏卷10)设三棱柱的侧棱垂直于底面,所有棱长都为
(2010年全国高考宁夏卷10)设三棱柱的侧棱垂直于底面,所有棱长都为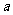 ,顶点都在一个球面上,则该球的表面积为
,顶点都在一个球面上,则该球的表面积为
(A) 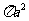 (B)
(B)
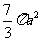 (C)
(C)
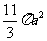 (D)
(D)
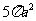
[答案]B
解析:如图,P为三棱柱底面中心,O为球心,易知
 ,所以球的半径
,所以球的半径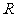 满足:
满足:
 ,故
,故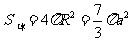 .
.
7.(2010年高考四川卷理科11)半径为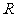 的球
的球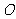 的直径
的直径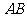 垂直于平面
垂直于平面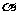 ,垂足为
,垂足为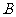 ,
,
 是平面
是平面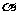 内边长为
内边长为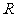 的正三角形,线段
的正三角形,线段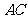 、
、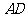 分别
分别
与球面交于点M,N,那么M、N两点间的球面距离是
 (A)
(A)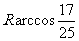 (B)
(B)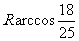 w_w_w.k*s 5*
w_w_w.k*s 5*
(C) (D)
(D)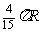
解析:由已知,AB=2R,BC=R,故tan∠BAC=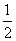 w_w_w.k*s 5*
w_w_w.k*s 5*
cos∠BAC=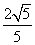
连结OM,则△OAM为等腰三角形
AM=2AOcos∠BAC=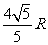 ,同理AN=
,同理AN=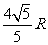 ,且MN∥CD w_w_w.k*s 5*
,且MN∥CD w_w_w.k*s 5*
而AC=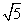 R,CD=R
R,CD=R
故MN:CD=AN:AC w_w_w.k*s 5*
Þ MN=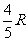 ,
,
连结OM、ON,有OM=ON=R
于是cos∠MON=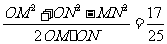
所以M、N两点间的球面距离是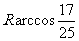 w_w_w.k*s 5*
w_w_w.k*s 5*
答案:A
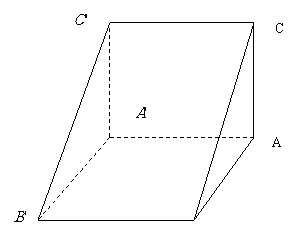
6.(2010年高考广东卷理科6)如图1,△ ABC为三角形,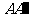 //
//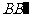 //
//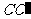 ,
, 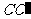 ⊥平面ABC 且3
⊥平面ABC 且3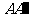 =
=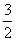
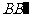 =
=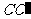 =AB,则多面体△ABC -
=AB,则多面体△ABC - 的正视图(也称主视图)是
的正视图(也称主视图)是

[答案]D
8.C
[解析]该几何体由两个长方体组合而成,其表面积等于下面长方体的全面积加上面长方体的4个侧面积之 和。
和。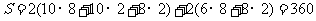 .
.
[方法技巧]把三视图转化为直观图是解决问题的关键.又三视图很容易知道是两个长方体的组合体,画出直观图,得出各个 棱的长度.把几何体的表面积转化为下面长方体的全面积加上面长方体的4个侧面积之和。
棱的长度.把几何体的表面积转化为下面长方体的全面积加上面长方体的4个侧面积之和。
5.(2010年高考安徽卷理科8)一个几何体的三视图如图,该几何体的表面积为
A、280 B、292 C、360 D、372
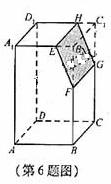
4.(2010年高考福建卷理科6)如图,若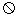 是长方体
是长方体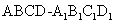 被平面
被平面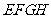 截去几何体
截去几何体 后得到的几何体,其中E为线段
后得到的几何体,其中E为线段 上异于
上异于 的点,F为线段
的点,F为线段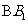 上异于
上异于 的点,且
的点,且 ∥
∥ ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.  ∥
∥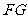 B.四边形
B.四边形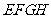 是矩形 C.
是矩形 C. 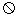 是棱柱 D.
是棱柱 D.  是棱台
是棱台
[答案]D
[解析]因为 ∥
∥ ,
, ∥
∥ ,所以
,所以 ∥
∥ ,又
,又
 平面
平面 ,
,
所以 ∥平面
∥平面 ,又
,又
 平面
平面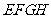 ,平面
,平面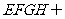 平面
平面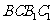 =
=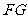 ,
,
所以 ∥
∥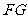 ,故
,故 ∥
∥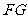 ∥
∥ ,所以选项A、C正确;因为
,所以选项A、C正确;因为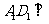 平面
平面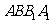 ,
,
 ∥
∥ ,所以
,所以
 平面
平面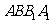 ,又
,又
 平面
平面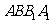 ,
故
,
故

 ,所以选项B也正确,故选D。
,所以选项B也正确,故选D。
 [命题意图]本题考查空间中直线与平面平行、垂直的判定与性质,考查同学们的空间想象能力和逻辑推理能力。
[命题意图]本题考查空间中直线与平面平行、垂直的判定与性质,考查同学们的空间想象能力和逻辑推理能力。
3.B[命题意图]本小题主要考查几何体的体积的计算、球的性质、异面直线的距离,通过球这个载体考查考生的空间想象能力及推理运算能力.
[解析]过CD作平面PCD,使AB⊥平面PCD,交AB与P,设点P到CD的距离为 ,则有
,则有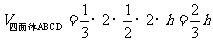 ,当直径通过AB与CD的中点时,
,当直径通过AB与CD的中点时,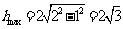 ,故
,故 .
.
3.( 2010年高考全国卷I理科12)已知在半径为2的球面上有A、B、C、D四点,若AB=CD=2,则四面体ABCD的体积的最大值为
(A) 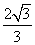 (B)
(B)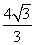 (C)
(C) 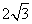 (D)
(D) 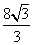
2. D [命题意图]本小题主要考查正方体的性质、直线与平面所成的角、点到平面的距离的求法,利用等体积转化求出D到平面AC
D [命题意图]本小题主要考查正方体的性质、直线与平面所成的角、点到平面的距离的求法,利用等体积转化求出D到平面AC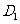 的距离是解决本题的关键所在,这也是转化思想的具体体现.
的距离是解决本题的关键所在,这也是转化思想的具体体现.
[解析]因为BB1//DD1,所以B 与平面AC
与平面AC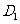 所成角和DD1与平面AC
所成角和DD1与平面AC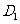 所成角相等,设DO⊥平面AC
所成角相等,设DO⊥平面AC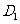 ,由等体积法得
,由等体积法得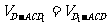 ,即
,即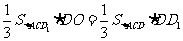 .设DD1=a,
.设DD1=a,
则 ,
,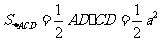 .
.
所以 ,记DD1与平面AC
,记DD1与平面AC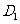 所成角为
所成角为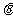 ,则
,则 ,所以
,所以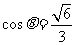 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com