
1.影响化学反应速率的最根本的因素是
A.催化剂 B.温度 C.反应物的性质 D.浓度
23.(本小题满分8分)已知{ an }是各项为正数的等比数列,且a1 = 1,a2 + a3 = 6,
求该数列前10项的和S10
24 (本小题满分8分)
(本小题满分8分)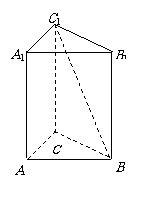 如图,在直三棱柱ABC
-A1B1C1 中,AB = AC
= 1,AA1 =
如图,在直三棱柱ABC
-A1B1C1 中,AB = AC
= 1,AA1 = 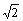 ,AB⊥AC
,AB⊥AC  求异面直线BC1与AC所成角的度数
求异面直线BC1与AC所成角的度数
25 (本小题满分8分)某化工厂生产的某种化工产品,当年产量在150吨至250吨之内,其年生产的总成本
(本小题满分8分)某化工厂生产的某种化工产品,当年产量在150吨至250吨之内,其年生产的总成本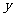 (万元)与年产量
(万元)与年产量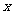 (吨)之间的关系可近似地表示为
(吨)之间的关系可近似地表示为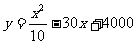 。
。
(1)当年产量为多少吨时,每吨的平均成本最低,并求每吨最低平均成本
(2)若每吨平均出厂价为16万元,求年生产多少吨时,可获得最大的年利润,并求最大年利润。
22.(本小题满分8分)求到两个定点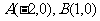 的距离之比等于2的点的轨迹方程。
的距离之比等于2的点的轨迹方程。
21.(本小题满分8分)设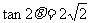 ,
,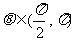 求
求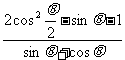 的值
的值
20.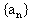 为等差数列,
为等差数列,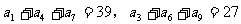 ,则
,则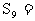 __________
__________
一、选择题答题卡:班级:_______姓名:___________考号:_______
16.函数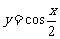 的最小正周期
的最小正周期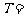
17 已知
已知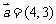 ,
,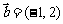 ,那么
,那么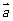 与
与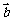 的夹角的余弦值为
的夹角的余弦值为
18 正方体的全面积是
正方体的全面积是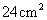 ,它的顶点都在一个球面上,则这个球的表面积是_________
,它的顶点都在一个球面上,则这个球的表面积是_________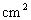 。
。
19 在△
在△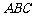 中,若
中,若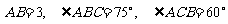 ,则
,则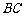 等于
等于
1 已知
已知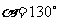 ,则
,则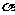 的终边在( )A
的终边在( )A 第一象限 B
第一象限 B 第二象限 C
第二象限 C 第三象限 D
第三象限 D 第四象限
第四象限
2 已知 f ( x ) =
已知 f ( x ) = 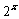 + 1 ,则 f ( 0 ) = ( )(A)-1 (B)0 (C) 1 (D)2
+ 1 ,则 f ( 0 ) = ( )(A)-1 (B)0 (C) 1 (D)2
3 算式
算式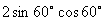 的值是( )A
的值是( )A
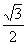 B
B
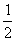 C
C
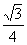 D
D
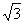
4 铁路旅行规定:旅客每人免费携带品的外部尺寸长
铁路旅行规定:旅客每人免费携带品的外部尺寸长 宽
宽 高之和不超过160厘米
高之和不超过160厘米 设携带品外部尺寸长宽
设携带品外部尺寸长宽
高分别为a,b,c (单位:厘米),这个规定用数学关系式可表示为( )
(A)a + b + c <160 (B)a + b + c >160 (C)a + b + c ≤ 160 (D)a + b + c ≥160
5 假设全集
假设全集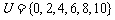 ,集合
,集合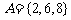 ,那么
,那么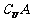 等于( )
等于( )
A.{4,8} B.{4,10} C.{0,4,8} D.{0,4,10}
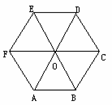
6 若
若 ,则下列各式正确的是( )
,则下列各式正确的是( )
 A
A
 B
B
 C
C
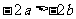 D
D
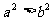
7 如图,在正六边形ABCDEF中,点O为其中点,则下列判断错误的是( )A
如图,在正六边形ABCDEF中,点O为其中点,则下列判断错误的是( )A
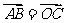 B
B
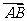 ∥
∥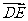 C
C
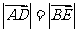 D
D
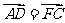
8 在空间中,下列命题正确的是(
)
在空间中,下列命题正确的是(
)
A 平行于同一平面的两条直线平行B
平行于同一平面的两条直线平行B 平行于同一直线的两个平面平行
平行于同一直线的两个平面平行
 C
C 垂直于同一直线的两条直线平行D
垂直于同一直线的两条直线平行D 垂直于同一平面的两条直线平行
垂直于同一平面的两条直线平行
9 圆心在
圆心在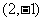 上,半径为3的圆的标准方程为( )
上,半径为3的圆的标准方程为( )
A
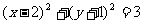 B
B
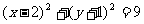
C
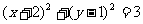 D
D
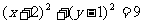
10 根据下面的流程图操作,使得当成绩不低于60分时,输出“及格”,
根据下面的流程图操作,使得当成绩不低于60分时,输出“及格”,
当成绩低于60分时,输出“不及格”,则( )
A.1框中填“Y”,2框中填“N” B.1框中填“N”,2框中填“Y”
C.1框中填“Y”,2框中可以不填 D.2框中填“N”,1框中可以不填
11 下列向量中,与
下列向量中,与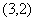 垂直的向量是( )A.
垂直的向量是( )A.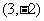 B.
B.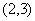 C.
C.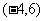 D.
D.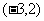
12 为检查某校学生心理健康状况,市教委从该校1400名学生中随机抽查400名学生,检查他们的心理健康程度,则下列说法正确的是( ) A.1400名学生的心理健康状况是总体 B.每个学生是个体
为检查某校学生心理健康状况,市教委从该校1400名学生中随机抽查400名学生,检查他们的心理健康程度,则下列说法正确的是( ) A.1400名学生的心理健康状况是总体 B.每个学生是个体
C.400名学生是总体的一个样本 D.400名学生为样本容量
13 将容量为100的样本数据,按从小到大的顺序分为8个组,如下表:
将容量为100的样本数据,按从小到大的顺序分为8个组,如下表:
|
组号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
频数 |
10 |
13 |
14 |
14 |
15 |
13 |
12 |
9 |
则第三组的频率和累积频率分别是( )A.0.14和0.37 B.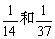 C.0.03和0.06 D.
C.0.03和0.06 D.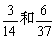
14 已知函数
已知函数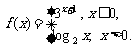 若
若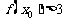 ,则
,则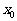 的取值范围是( )
的取值范围是( )
(A)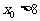 . (B)
. (B)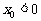 或
或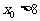 . (C)
. (C)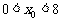 .
(D)
.
(D)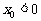 或
或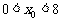 .
.
15 已知
已知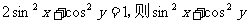 的取值范围为( )
的取值范围为( )
A. 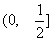 B.
B.
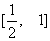 C.
C.
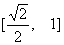 D.
D.
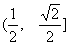
(17)(本小题满分12分)
某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为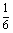 .甲、乙、丙三位同学每人购买了一瓶该饮料。
.甲、乙、丙三位同学每人购买了一瓶该饮料。
(Ⅰ)求甲中奖且乙、丙都没有中奖的概率;
(Ⅱ)求中奖人数ξ的分布列及数学期望Eξ.

解:显然甲、乙、丙三位同学是否中奖独立,所以甲中奖且乙、丙都没有中奖的概率是: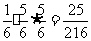
(2)
|
ξ |
0 |
1 |
2 |
3 |
|
P |
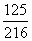 [来源:Z&xx&] [来源:Z&xx&] |
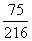  |
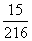 |
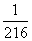 |
Eξ=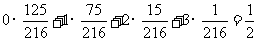
(18)(本小题满分12分)

 w_w w. k#s5_
w_w w. k#s5_
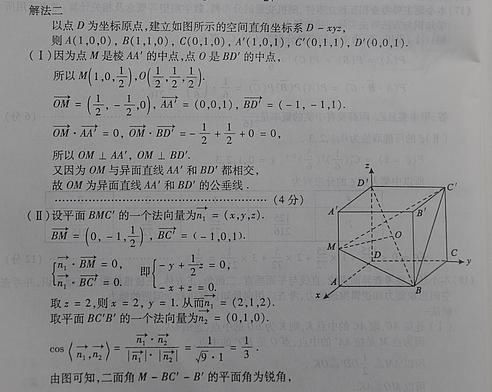
已知正方体ABCD-A'B'C'D'的棱长为1,点M是棱AA'的中点,点O是对角线BD'的中点.
(Ⅰ)求证:OM为异面直线AA'和BD'的公垂线;

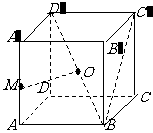 (Ⅱ)求二面角M-BC'-B'的大小;
(Ⅱ)求二面角M-BC'-B'的大小;
(Ⅲ)求三棱锥M-OBC的体积.



(19)(本小题满分12分)
(Ⅰ)1证明两角和的余弦公式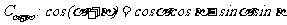 ;
;
2由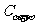 推导两角和的正弦公式
推导两角和的正弦公式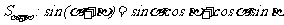 .
.
(Ⅱ)已知△ABC的面积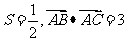 ,且
,且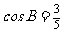 ,求cosC.
,求cosC.

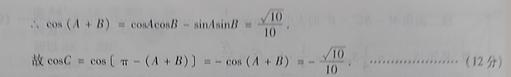
(20)(本小题满分12分)
已知定点A(-1,0),F(2,0),定直线l:x=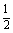 ,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E,过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N
,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E,过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N
(Ⅰ)求E的方程;
(Ⅱ)试判断以线段MN为直径的圆是否过点F,并说明理由.

(21)(本小题满分12分)
已知数列{an}满足a1=0,a2=2,且对任意m、n∈N*都有
a2m-1+a2n-1=2am+n-1+2(m-n)2
(Ⅰ)求a3,a5;
(Ⅱ)设bn=a2n+1-a2n-1(n∈N*),证明:{bn}是等差数列;
(Ⅲ)设cn=(an+1-an)qn-1(q≠0,n∈N*),求数列{cn}的前n项和Sn.

(22)(本小题满分14分)
设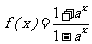 (
(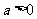 且
且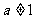 ),g(x)是f(x)的反函数.
),g(x)是f(x)的反函数.
(Ⅰ)设关于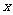 的方程求
的方程求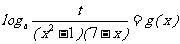 在区间[2,6]上有实数解,求t的取值范围;
在区间[2,6]上有实数解,求t的取值范围;
(Ⅱ)当a=e(e为自然对数的底数)时,证明: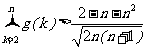 ;
;
(Ⅲ)当0<a≤时,试比较 与4的大小,并说明理由.
与4的大小,并说明理由.


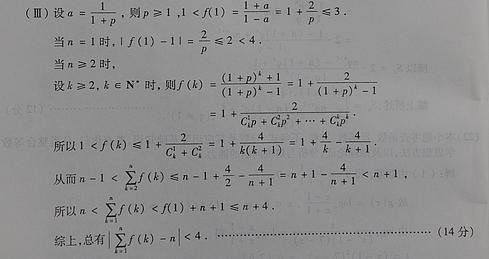
(13)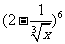 的展开式中的第四项是
. w_w_w.k*s 5*
的展开式中的第四项是
. w_w_w.k*s 5*
解析:T4=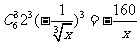 w_w_w.k*s 5*
w_w_w.k*s 5*
答案:-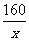
(14)直线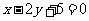 与圆
与圆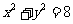 相交于A、B两点,则
相交于A、B两点,则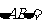 .
.
解析:方法一、圆心为(0,0),半径为2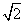
圆心到直线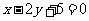 的距离为d=
的距离为d=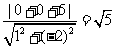


 w_w w. k#s5_
w_w w. k#s5_
故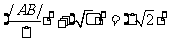 w_w_w.k*s 5*
w_w_w.k*s 5*
得|AB|=2
答案:2
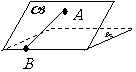 (15)如图,二面角
(15)如图,二面角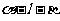 的大小是60°,线段
的大小是60°,线段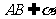 .
.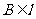 ,
,
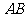 与
与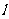 所成的角为30°.则
所成的角为30°.则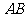 与平面
与平面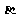 所成的角的正弦值是
.
所成的角的正弦值是
.
解析:过点A作平面β的垂线,垂足为C,在β内过C作l的垂线.垂足为D
连结AD,有三垂线定理可知AD⊥l,
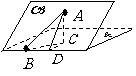 故∠ADC为二面角
故∠ADC为二面角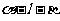 的平面角,为60°
的平面角,为60°
又由已知,∠ABD=30°
连结CB,则∠ABC为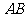 与平面
与平面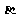 所成的角w_w_w.k*s 5*
所成的角w_w_w.k*s 5*
设AD=2,则AC=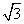 ,CD=1
,CD=1
AB=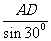 =4
=4
∴sin∠ABC=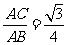
答案: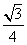
(16)设S为复数集C的非空子集.若对任意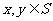 ,都有
,都有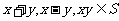 ,则称S为封闭集。下列命题:
,则称S为封闭集。下列命题:
①集合S={a+bi|(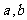 为整数,
为整数,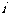 为虚数单位)}为封闭集;w_w_w.k*s 5*
为虚数单位)}为封闭集;w_w_w.k*s 5*
②若S为封闭集,则一定有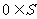 ;
;
③封闭集一定是无限集;
④若S为封闭集,则满足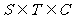 的任意集合
的任意集合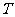 也是封闭集.
也是封闭集. 

 w_w w. k#s5_
w_w w. k#s5_
其中真命题是 (写出所有真命题的序号)
解析:直接验证可知①正确.
当S为封闭集时,因为x-y∈S,取x=y,得0∈S,②正确
对于集合S={0},显然满足素有条件,但S是有限集,③错误
取S={0},T={0,1},满足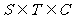 ,但由于0-1=-1ÏT,故T不是封闭集,④错误
,但由于0-1=-1ÏT,故T不是封闭集,④错误
答案:①②
(1)i是虚数单位,计算i+i2+i3=
(A)-1 (B)1
(C) (D)
(D)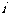
解析:由复数性质知:i2=-1
故i+i2+i3=i+(-1)+(-i)=-1
答案:A
(2)下列四个图像所表示的函数,在点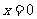 处连续的是
处连续的是
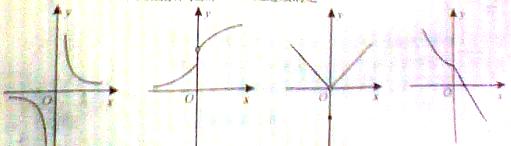
(A) (B) (C) (D)
解析:由图象及函数连续的性质知,D正确.w_w_w.k*s 5*
答案:D
(3)2log510+log50.25=w_w_w.k*s 5*
(A)0 (B)1
(C) 2
(D)4

 w_w w. k#s5_
w_w w. k#s5_
解析:2log510+log50.25
=log5100+log50.25
=log525
=2
答案:C
(4)函数f(x)=x2+mx+1的图像关于直线x=1对称的充要条件是
(A)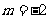 (B)
(B)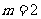 (C)
(C)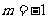 (D)
(D)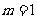
解析:函数f(x)=x2+mx+1的对称轴为x=-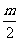 w_w_w.k*s 5*
w_w_w.k*s 5*
于是-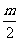 =1 Þ m=-2
=1 Þ m=-2
答案:A
(5)设点M是线段BC的中点,点A在直线BC外,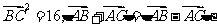 则
则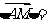
(A)8 (B)4
(C) 2
(D)1

 w_w w. k#s5_
w_w w. k#s5_
解析:由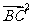 =16,得|BC|=4 w_w_w.k*s 5*
=16,得|BC|=4 w_w_w.k*s 5*
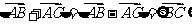 =4
=4
而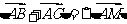
故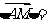 2
2
答案:C w_w_w.k*s 5*
(6)将函数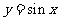 的图像上所有的点向右平行移动
的图像上所有的点向右平行移动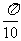 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是

 w_w w. k#s5_
w_w w. k#s5_
(A)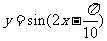 (B)
(B)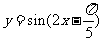 w_w_w.k*s 5*
w_w_w.k*s 5*
(C)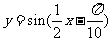 (D)
(D)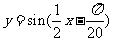
解析:将函数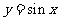 的图像上所有的点向右平行移动
的图像上所有的点向右平行移动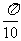 个单位长度,所得函数图象的解析式为y=sin(x-
个单位长度,所得函数图象的解析式为y=sin(x-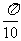 ) w_w_w.k*s 5*
) w_w_w.k*s 5*
再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是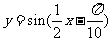 .
.
答案:C
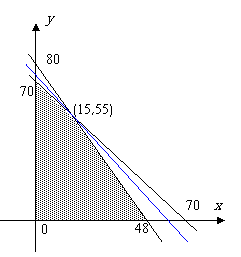 (7)某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品,每千克A产品获利40元,乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙两车间耗费工时总和不得超过480小时,甲、乙两车间每天总获利最大的生产计划为w_w_w.k*s 5*
(7)某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品,每千克A产品获利40元,乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙两车间耗费工时总和不得超过480小时,甲、乙两车间每天总获利最大的生产计划为w_w_w.k*s 5*
(A)甲车间加工原料10箱,乙车间加工原料60箱
(B)甲车间加工原料15箱,乙车间加工原料55箱
(C)甲车间加工原料18箱,乙车间加工原料50箱
(D)甲车间加工原料40箱,乙车间加工原料30箱
解析:设甲车间加工原料x箱,乙车间加工原料y箱
则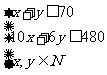


 w_w w. k#s5_
w_w w. k#s5_
目标函数z=280x+300y
结合图象可得:当x=15,y=55时z最大
本题也可以将答案逐项代入检验.
答案:B w_w_w.k*s 5*
(8)已知数列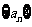 的首项
的首项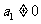 ,其前
,其前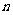 项的和为
项的和为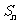 ,且
,且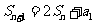 ,则
,则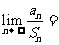
(A)0 (B)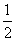 (C) 1
(D)2
(C) 1
(D)2
解析:由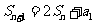 ,且
,且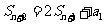 w_w_w.k*s 5*
w_w_w.k*s 5*
作差得an+2=2an+1
又S2=2S1+a1,即a2+a1=2a1+a1 Þ a2=2a1

 w_w w. k#s5_
w_w w. k#s5_
故{an}是公比为2的等比数列
Sn=a1+2a1+22a1+……+2n-1a1=(2n-1)a1
则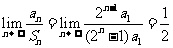
答案:B
(9)椭圆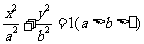 的右焦点
的右焦点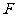 ,其右准线与
,其右准线与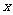 轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点
轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点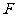 ,则椭圆离心率的取值范围是w_w_w.k*s 5*
,则椭圆离心率的取值范围是w_w_w.k*s 5*
(A)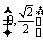 (B)
(B)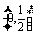 (C)
(C) 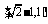 (D)
(D)
解析:由题意,椭圆上存在点P,使得线段AP的垂直平分线过点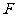 ,
,
即F点到P点与A点的距离相等

 w_w w. k#s5_
w_w w. k#s5_
而|FA|=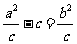 w_w_w.k*s 5*
w_w_w.k*s 5*
|PF|∈[a-c,a+c]
于是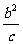 ∈[a-c,a+c]
∈[a-c,a+c]
即ac-c2≤b2≤ac+c2
∴
Þ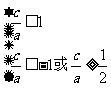 w_w_w.k*s 5*
w_w_w.k*s 5*
又e∈(0,1)
故e∈
答案:D
(10)由1、2、3、4、5、6组成没有重复数字且1、3都不与5相邻的六位偶数的个数是
(A)72 (B)96 (C) 108 (D)144 w_w_w.k*s 5*
解析:先选一个偶数字排个位,有3种选法w_w_w.k*s 5*
①若5在十位或十万位,则1、3有三个位置可排,3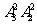 =24个
=24个
②若5排在百位、千位或万位,则1、3只有两个位置可排,共3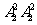 =12个
=12个
 算上个位偶数字的排法,共计3(24+12)=108个
算上个位偶数字的排法,共计3(24+12)=108个
答案:C
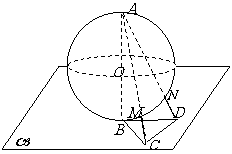
(11)半径为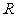 的球
的球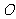 的直径
的直径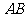 垂直于平面
垂直于平面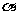 ,垂足为
,垂足为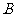 ,
,
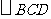 是平面
是平面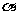 内边长为
内边长为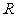 的正三角形,线段
的正三角形,线段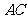 、
、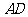 分别
分别
与球面交于点M,N,那么M、N两点间的球面距离是
(A)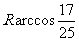 (B)
(B)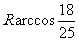 w_w_w.k*s 5*
w_w_w.k*s 5*
(C)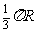 (D)
(D)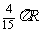
解析:由已知,AB=2R,BC=R,故tan∠BAC=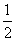 w_w_w.k*s 5*
w_w_w.k*s 5*
cos∠BAC=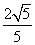
连结OM,则△OAM为等腰三角形
AM=2AOcos∠BAC=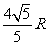 ,同理AN=
,同理AN=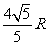 ,且MN∥CD w_w_w.k*s 5*
,且MN∥CD w_w_w.k*s 5*
而AC=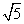 R,CD=R
R,CD=R
故MN:CD=AN:AC w_w_w.k*s 5*
Þ MN=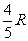 ,
,
连结OM、ON,有OM=ON=R
于是cos∠MON=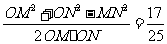
所以M、N两点间的球面距离是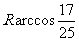 w_w_w.k*s 5*
w_w_w.k*s 5*
答案:A
(12)设 ,则
,则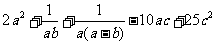 的最小值是
的最小值是

 w_w w. k#s5_
w_w w. k#s5_
(A)2 (B)4 (C) 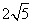 (D)5
(D)5
解析: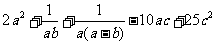
=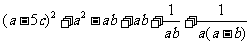 w_w_w.k*s 5*
w_w_w.k*s 5*
=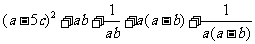
≥0+2+2=4
当且仅当a-5c=0,ab=1,a(a-b)=1时等号成立
如取a=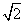 ,b=
,b=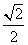 ,c=
,c=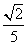 满足条件.
满足条件.
答案:B
第Ⅱ卷
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com