
26. 直线 与
与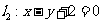 垂直,则
垂直,则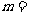 __1____.
__1____.
25. 直线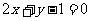 的倾斜角大小为__
的倾斜角大小为__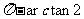 ___(用反三角形式表示).
___(用反三角形式表示).
24. 已知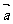 ,
,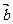 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为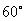 ,则
,则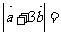 __
__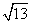 _____.
_____.
23. 袋中有3只相同的白球和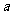 只相同的黑球,从中任取2只,恰好一白一黑的概率为
只相同的黑球,从中任取2只,恰好一白一黑的概率为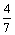 ,则
,则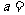 4 .
4 .
22. 在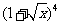 的展开式中,
的展开式中,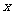 的系数为 6 (用数字作答).
的系数为 6 (用数字作答).
21. (12分) 我国计划发射火星探测器,该探测器的运行轨道是以火星(其半径
我国计划发射火星探测器,该探测器的运行轨道是以火星(其半径 百公里)的中心
百公里)的中心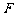 为一个焦点的椭圆. 如图,已知探测器的近火星点(轨道上离火星表面最近的点)
为一个焦点的椭圆. 如图,已知探测器的近火星点(轨道上离火星表面最近的点) 到火星表面的距离为
到火星表面的距离为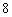 百公里,远火星点(轨道上离火星表面最远的点)
百公里,远火星点(轨道上离火星表面最远的点)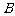 到火星表面的距离为800百公里. 假定探测器由近火星点
到火星表面的距离为800百公里. 假定探测器由近火星点 第一次逆时针运行到与轨道中心
第一次逆时针运行到与轨道中心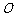 的距离为
的距离为 百公里时进行变轨,其中
百公里时进行变轨,其中 、
、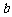 分别为椭圆的长半轴、短半轴的长,求此时探测器与火星表面的距离(精确到1百公里).
分别为椭圆的长半轴、短半轴的长,求此时探测器与火星表面的距离(精确到1百公里).
解:
上海市松江二中2009学年第二学期高二数学五月考
(本试卷共有21道试题,满分100分,考试时间90分钟。)
20. (12分)已知点(x, y)是曲线C上任意一点,将此点的纵坐标变为原来的2倍,对应的横坐标不变,得到的点满足方程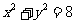 ;定点M(2,1),平行于OM的直线
;定点M(2,1),平行于OM的直线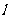 在y轴上的截距为m(m≠0),直线
在y轴上的截距为m(m≠0),直线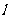 与曲线C交于A、B两个不同点.
与曲线C交于A、B两个不同点.
(1)求曲线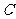 的方程;
的方程;
(2)求m的取值范围.
解:
19.
(12分)已知函数 ,
,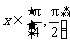 .
.
(1)求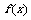 的最大值和最小值;
的最大值和最小值;
(2)若不等式 在
在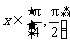 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
解:
18. (8分)由直线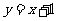 上的点A向圆
上的点A向圆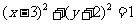 引切线,切点为P,求
引切线,切点为P,求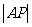 的最小值.
的最小值.
解:
17. (8分)已知A(3,2),B(-2,7),若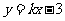 与线段AB相交,求
与线段AB相交,求 的取值范围.
的取值范围.
解:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com