
1、2010年1月31日,新华社受权发布《中共中央、国务院关于加大统筹城乡发展力度,进一步夯实农业农村发展发展基础的若干意见》,这是新世纪以来指导“三农”工作的第 个中央一号文件。
A、6 B、7 C、8 D、9
21.(本小题满分14分)
已知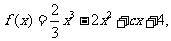
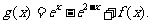
(Ⅰ)若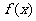 在
在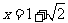 处取得极值,试求
处取得极值,试求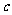 的值和
的值和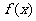 的单调增区间;
的单调增区间;
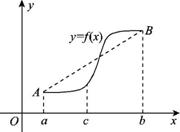 (Ⅱ)如图所示,若函数
(Ⅱ)如图所示,若函数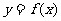 的图像在
的图像在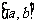 上连续光滑,试猜想拉格朗日中值定理:即一定存在
上连续光滑,试猜想拉格朗日中值定理:即一定存在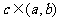 使得
使得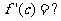 (用含有
(用含有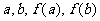 的表达方式直接回答,不需要写猜想过程)
的表达方式直接回答,不需要写猜想过程)
(Ⅲ)利用(Ⅱ)证明:函数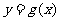 图像上任意两点的连线斜率不小于
图像上任意两点的连线斜率不小于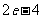 .
.
20.(本小题满分13分)
已知四棱锥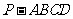 中,
中,
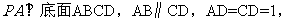
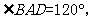
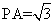 ,
,
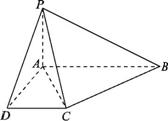
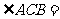 90°.
90°.
(Ⅰ)求证: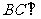 平面
平面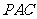 ;
;
(Ⅱ)求直线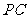 与平面
与平面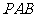 所成的角的正弦值.
所成的角的正弦值.
19. (本小题满分12分)
设数列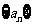 的首项
的首项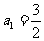 ,前
,前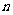 项和为
项和为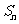 ,且满足
,且满足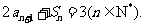
(Ⅰ)求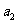 及
及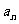 ;
;
(Ⅱ)求满足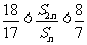 的所有
的所有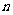 的值.
的值.
18.(本小题满分15分)
已知直线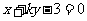 所经过的定点
所经过的定点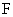 恰好是椭圆
恰好是椭圆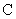 的一个焦点,且椭圆
的一个焦点,且椭圆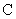 上的点到点
上的点到点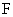 的最大距离为8.
的最大距离为8.
(Ⅰ)求椭圆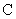 的标准方程;
的标准方程;
(Ⅱ)已知圆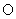 :
: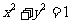 ,直线
,直线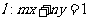 .试证:当点
.试证:当点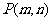 在椭圆
在椭圆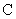 上运动时,直线
上运动时,直线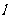 与圆
与圆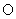 恒相交,并求直线
恒相交,并求直线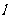 被圆
被圆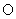 所截得弦长
所截得弦长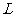 的取值范围.
的取值范围.
17.(本小题满分12分)
某研究机构为了研究人的脚的大小与身高之问的关系,随机抽测了20人,得到如下数据:
|
序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
身高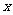 (厘米) (厘米) |
192 |
164 |
172 |
177 |
176 |
159 |
171 |
166 |
182 |
166 |
脚长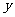 (码) (码) |
48 |
38 |
40 |
43 |
44 |
37 |
40 |
39 |
46 |
39 |
|
序号 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
身高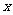 (厘米) (厘米) |
169 |
178 |
167 |
174 |
168 |
179 |
165 |
170 |
162 |
170 |
脚长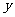 (码) (码) |
43 |
41 |
40 |
43 |
40 |
44 |
38 |
42 |
39 |
41 |
(Ⅰ)若“身高大于l75厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”;“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”.请根据上表数据完成下面的2×2列联表:
|
|
高个 |
非高个 |
合计 |
|
大脚 |
|
|
|
|
非大脚 |
|
12 |
|
|
合计 |
|
|
20 |
(Ⅱ)根据题(I)中表格的数据,若按99%的可靠性要求,能否认为脚的大小与身高之间有关系?
(Ⅲ)若按下面的方法从这20人中抽取1人来核查测量数据的误差:将一个标有数字1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号.试求:①抽到12号的概率;②抽到“无效序号(超过20号)”的概率.
16.(本小题满分12分)
已知在锐角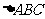 中,角
中,角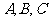 的对边分别为
的对边分别为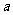 ,
,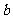 ,
,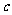 且
且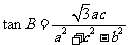 ,
,
(Ⅰ)求B;
(Ⅱ)求函数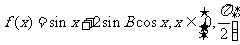 的单调递减区间.
的单调递减区间.
15. 已知椭圆的中心为原点,离心率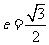 ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线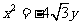 的焦点重合,则此椭圆方程为
.
的焦点重合,则此椭圆方程为
.
14. 已知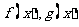 都是定义在
都是定义在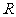 上的函数,且满足以下条件:
上的函数,且满足以下条件:
①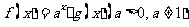 ;②
;②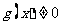 ;③
;③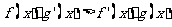 ;若
;若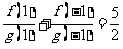 ,则
,则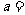 ________.
________.
13. 函数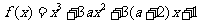 有极大值又有极小值,则a的范围是
.
有极大值又有极小值,则a的范围是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com