(三)自主学习、加深认识

练习：教材第59页1、2、3题。

学生先独立完成后，教师指导讲评。

(二)研探新知

1、问题：

(1)平面β内有一条直线与平面α平行，α、β平行吗？

(2)平面β内有两条直线与平面α平行，α、β平行吗？

通过长方体模型，引导学生观察、思考、交流，得出结论。

两个平面平行的判定定理：一个平面内的两条交直线与另一个平面平行，则这两个平面平行。

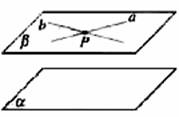
符号表示：

a　 β

b　 β

a∩b = P　 β∥α

a∥α

b∥α

教师指出：判断两平面平行的方法有三种：

(1)用定义；

(2)判定定理；

(3)垂直于同一条直线的两个平面平行。

2、例2 引导学生思考后，教师讲授。

例子的给出，有利于学生掌握该定理的应用。

(一)创设情景、引入课题

引导学生观察、思考教材第57页的观察题，导入本节课所学主题。

2、教学用具：投影仪、投影片、长方体模型

1、学法：学生借助实物，通过观察、类比、思考、探讨，教师予以启发，得出两平面平行的判定。

重点：两个平面平行的判定。

难点：判定定理、例题的证明。

3、情感、态度与价值观

进一步培养学生空间问题平面化的思想。

2、过程与方法

让学生通过观察实物及模型，得出两平面平行的判定。

1、知识与技能

理解并掌握两平面平行的判定定理。

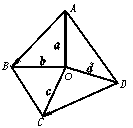
4、如图所示，O是四边形ABCD内任一点，试根据图中给出的向量，确定a、b、c、d的方向(用箭头表示)，使a+b=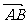，c-d=，并画出b-c和a+d.