
|
课题 一、知识点 (一) |
(二) |
例题: 1. |
2. |
3.函数y=ksinx+b的最大值为2, 最小值为-4,求k,b的值。
2. 求下列函数的最值: 1° y=sin(3x+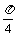 )-1
2° y=sin2x-4sinx+5 3° y=
)-1
2° y=sin2x-4sinx+5 3° y=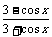
补充:
1.求下列函数的周期:
1°y=sin(2x+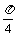 )+2cos(3x-
)+2cos(3x-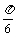 )
2° y=|sinx| 3° y=2
)
2° y=|sinx| 3° y=2 sinxcosx+2cos2x-1
sinxcosx+2cos2x-1
周期函数的定义,周期,最小正周期
4. y=cos sin
sin +1-2sin2
+1-2sin2
3. y=|sin(2x+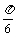 )|
)|
2. y=-cos(3x+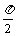 )+sin(4x-
)+sin(4x-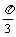 )
)
1. y=2cos(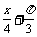 )-3sin(
)-3sin(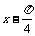 )
)
3、例题讲解
例1 求下列三角函数的周期: ①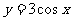 ②
② (3)
(3)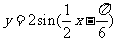 ,
, .
.
解:(1)∵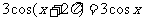 ,
,
∴自变量 只要并且至少要增加到
只要并且至少要增加到 ,函数
,函数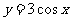 ,
, 的值才能重复出现,
的值才能重复出现,
所以,函数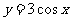 ,
, 的周期是
的周期是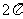 .
.
(2)∵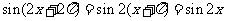 ,
,
∴自变量 只要并且至少要增加到
只要并且至少要增加到 ,函数
,函数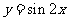 ,
, 的值才能重复出现,
的值才能重复出现,
所以,函数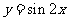 ,
, 的周期是
的周期是 .
.
(3)∵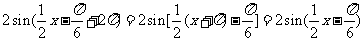 ,
,
∴自变量 只要并且至少要增加到
只要并且至少要增加到 ,函数
,函数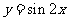 ,
, 的值才能重复出现,
的值才能重复出现,
所以,函数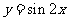 ,
, 的周期是
的周期是 .
.
说明:(1)一般结论:函数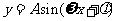 及函数
及函数 ,
, (其中
(其中 为常数,且
为常数,且 ,
, )的周期
)的周期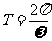 ;
;
(2)若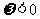 ,例如:①
,例如:① ,
, ;②
;② ,
, ;
;
③ ,
, .
.
则这三个函数的周期又是什么?
一般结论:函数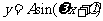 及函数
及函数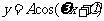 ,
, 的周期
的周期
例2先化简,再求函数的周期
① ②
②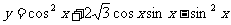 ③证明函数
③证明函数 的一个周期为
的一个周期为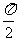 ,并求函数的值域;
,并求函数的值域;
例3 求下列三角函数的周期:
1° y=sin(x+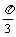 ) 2° y=cos2x 3° y=3sin(
) 2° y=cos2x 3° y=3sin(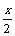 +
+ )
)
解:1° 令z= x+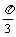 而 sin(2p+z)=sinz
即:f (2p+z)=f (z)
而 sin(2p+z)=sinz
即:f (2p+z)=f (z)
f [(x+2)p+ 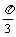 ]=f (x+
]=f (x+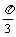 )
∴周期T=2p
)
∴周期T=2p
2°令z=2x ∴f (x)=cos2x=cosz=cos(z+2p)=cos(2x+2p)=cos[2(x+p)]
即:f (x+p)=f (x) ∴T=p
3°令z=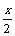 +
+ 则:f (x)=3sinz=3sin(z+2p)=3sin(
则:f (x)=3sinz=3sin(z+2p)=3sin(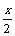 +
+ +2p)
+2p)
=3sin(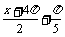 )=f (x+4p)
∴T=4p
)=f (x+4p)
∴T=4p
小结:形如y=Asin(ωx+φ) (A,ω,φ为常数,A¹0, xÎR) 周期T=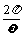
y=Acos(ωx+φ)也可同法求之
例4 求下列函数的周期: 1°y=sin(2x+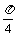 )+2cos(3x-
)+2cos(3x-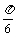 )
)
2° y=|sinx| 3° y=2 sinxcosx+2cos2x-1
sinxcosx+2cos2x-1
解:1° y1=sin(2x+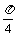 ) 最小正周期T1=p
) 最小正周期T1=p
y2=2cos(3x-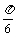 ) 最小正周期 T2=
) 最小正周期 T2=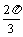
∴T为T1 ,T2的最小公倍数2p ∴T=2p
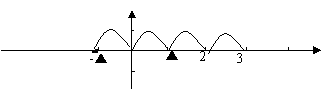 2°
T=p 作图
2°
T=p 作图
注意小结这两种类型的解题规律
3° y= sin2x+cos2x ∴T=p
sin2x+cos2x ∴T=p
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com