
8.(2008年江西卷2)定义集合运算: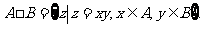 设
设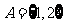 ,
,
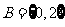 ,则集合
,则集合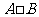 的所有元素之和为 ( )
的所有元素之和为 ( )
A.0 B.2 C.3 D.6
答案 D
7.(2007年安徽)若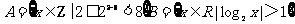 ,则
,则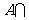 (RB)的
(RB)的
元素个数为 ( )
A.0 B.1 C.2 D.3
答案 C
6.(2007年江西)若集合M={0,l,2},N={(x,y)|x-2y+1≥0且x-2y-1≤0,x,
y∈M},则N中元素的个数为 ( )
A.9 B.6 C.4 D.2
答案 C
5.(2007年全国Ⅰ)设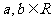 ,集合
,集合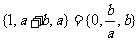 ,则
,则 ( )
( )
A.1
B. C.2
D.
C.2
D.
答案 C
4.(2008年山东卷1)满足M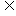 {a1,a2,a3,a4},且M∩{a1 ,a2,
a3}={a1,a2}的集合M的个数是 ( )
{a1,a2,a3,a4},且M∩{a1 ,a2,
a3}={a1,a2}的集合M的个数是 ( )
A.1 B.2 C.3 D.4
答案 B
3.(2008年全国II理1文)设集合M={m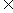 Z|-3<m<2},N={n
Z|-3<m<2},N={n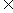 Z|-1≤n≤3},
Z|-1≤n≤3},
则M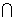 N ( )
N ( )
A.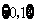 B.
B.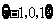 C.
C. D.
D.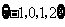
答案 B
解析 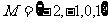 ,
,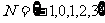 ,∴
,∴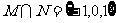 选B.
选B.
高考考点 集合的运算,整数集的符号识别
2.(2008年四川卷1)设集合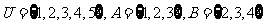 ,则
,则
u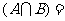 ( )
( )
A.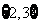 B.
B.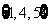 C.
C.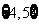 D.
D.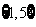
答案 B
1.(2008年北京卷1)已知全集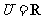 ,集合
,集合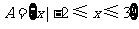
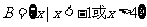 ,那么集合
,那么集合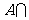 (uB等于 ( )
(uB等于 ( )
A.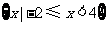 B.
B.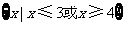
C.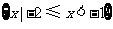 D.
D.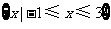
答案 D
35.(2009湖南卷文)某班共30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为 12 .
解: 设所求人数为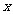 ,则只喜爱乒乓球运动的人数为
,则只喜爱乒乓球运动的人数为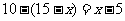 ,
,
故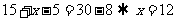 . 注:最好作出韦恩图!
. 注:最好作出韦恩图!
2005-2008年高考题
34..(2009湖南卷理)某班共30人,其中15人喜爱篮球运动,10人喜爱兵乓球运动,8人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为_12__
答案 :12
解析 设两者都喜欢的人数为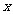 人,则只喜爱篮球的有
人,则只喜爱篮球的有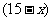 人,只喜爱乒乓球的有
人,只喜爱乒乓球的有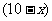 人,由此可得
人,由此可得 ,解得
,解得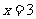 ,所以
,所以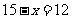 ,即 所求人数为12人。
,即 所求人数为12人。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com