
7.(2006年北京卷14)某校数学课外小组在坐标纸上,为学校的一块空地设计植树方案如下:第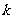 棵树种植在点
棵树种植在点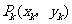 处,其中
处,其中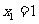 ,
,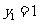 ,当
,当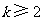 时,
时,
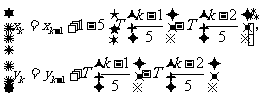
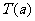 表示非负实数
表示非负实数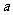 的整数部分,例如
的整数部分,例如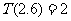 ,
,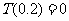 .按此方案,第6棵树种植点的坐标应为 ;第2008棵树种植点的坐标应为 .
.按此方案,第6棵树种植点的坐标应为 ;第2008棵树种植点的坐标应为 .
答案 (1,2)(3,402)
6.(2007年上海4)方程 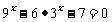 的解是 .
的解是 .
答案 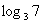
5.(2006年上海春季2)方程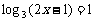 的解
的解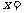 .
.
答案 2
4.某地一年内的气温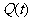 (单位:℃)与时刻
(单位:℃)与时刻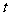 (月份)之间的关系如图所示,已知该年的平均气温为10℃ .令C(t)表示的时间段[0,t]的平均气温,
(月份)之间的关系如图所示,已知该年的平均气温为10℃ .令C(t)表示的时间段[0,t]的平均气温,
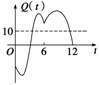 C(t)与t之间的函数关系用下列图象表示,则正确的应该是 ( )
C(t)与t之间的函数关系用下列图象表示,则正确的应该是 ( )
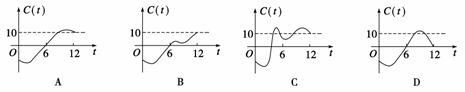
答案 A
解析 由图可以发现当t=6时,C(t)=0,排除C;t=12时,C(t)=10,排除D;t在大于6 的某一段气温超于10,所以排除B,故选A。
3.(07广东)客车从甲地以60km/h的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km/h的速度匀速行驶1小时到达丙地,下列描述客车从甲地出发.经过乙地,最后到达丙地所经过的路程s与时间t之间关系的图象中,正确的是 ( )
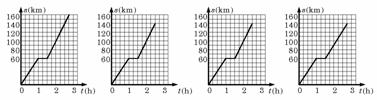
A B C D
答案 C
2.(2008年福建卷12)已知函数y=f(x),y=g(x)的导函数的图象如下图,那么y=f(x),y=g(x)
的图象可能是 ( )
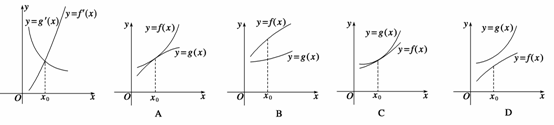
答案 D
1.(2008年全国一2)汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一
过程中汽车的行驶路程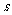 看作时间
看作时间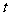 的函数,其图像可能是 ( )
的函数,其图像可能是 ( )
答案 A
7.(2009上海卷文)(本题满分16分)本题共有2个小题,第1小题满分6分,第2小题满分10分 .有时可用函数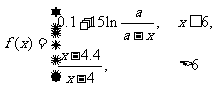
描述学习某学科知识的掌握程度.其中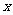 表示某学科知识的学习次数(
表示某学科知识的学习次数(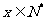 ),
),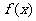 表示对该学科知识的掌握程度,正实数a与学科知识有关.
表示对该学科知识的掌握程度,正实数a与学科知识有关.
(1)证明:当x  7时,掌握程度的增长量f(x+1)- f(x)总是下降;
7时,掌握程度的增长量f(x+1)- f(x)总是下降;
(2)根据经验,学科甲、乙、丙对应的a的取值区间分别为(115,121],(121,127],
(127,133].当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
证明 (1)当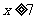 时,
时,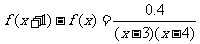
而当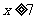 时,函数
时,函数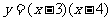 单调递增,且
单调递增,且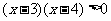
故函数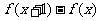 单调递减
单调递减
当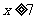 时,掌握程度的增长量
时,掌握程度的增长量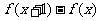 总是下降
总是下降
(2)有题意可知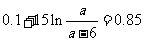
整理得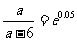
解得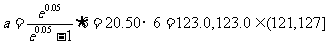 …….13分
…….13分
由此可知,该学科是乙学科……………..14分
2005-2008年高考题
6.(2009年上海卷理)有时可用函数
描述学习某学科知识的掌握程度,其中x表示某学科知识的学习次数(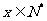 ),
),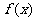 表示对该学科知识的掌握程度,正实数a与学科知识有关。
表示对该学科知识的掌握程度,正实数a与学科知识有关。
(1)证明 当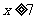 时,掌握程度的增加量
时,掌握程度的增加量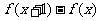 总是下降;
总是下降;
(2)根据经验,学科甲、乙、丙对应的a的取值区间分别为
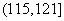 ,
,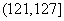 ,
,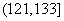 。当学习某学科知识6次时,掌握程度是85%,请确定相应的学科。
。当学习某学科知识6次时,掌握程度是85%,请确定相应的学科。
证明 (1)当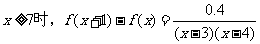
而当 ,函数
,函数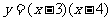 单调递增,且
单调递增,且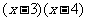 >0……..3分
>0……..3分
故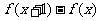 单调递减
单调递减
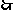 当
当 ,掌握程度的增长量
,掌握程度的增长量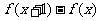 总是下降……………..6分
总是下降……………..6分
(2)由题意可知0.1+15ln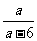 =0.85……………….9分
=0.85……………….9分
整理得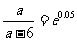
解得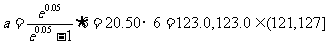 …….13分
…….13分
由此可知,该学科是乙学科……………..14分
5. (2009湖南卷理)(本小题满分13分)
某地建一座桥,两端的桥墩已建好,这两墩相距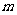 米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为
米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为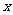 米的相邻两墩之间的桥面工程费用为
米的相邻两墩之间的桥面工程费用为 万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为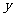 万元。
万元。
(Ⅰ)试写出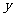 关于
关于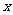 的函数关系式;
的函数关系式;
(Ⅱ)当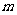 =640米时,需新建多少个桥墩才能使
=640米时,需新建多少个桥墩才能使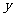 最小?
最小?
解 (Ⅰ)设需要新建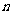 个桥墩,
个桥墩,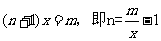
所以 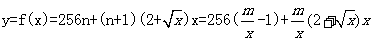
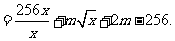
(Ⅱ) 由(Ⅰ)知,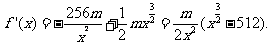
令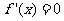 ,得
,得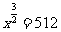 ,所以
,所以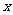 =64
=64
当0<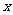 <64时
<64时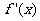 <0,
<0, 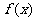 在区间(0,64)内为减函数;
在区间(0,64)内为减函数;
当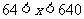 时,
时,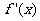 >0.
>0. 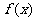 在区间(64,640)内为增函数,
在区间(64,640)内为增函数,
所以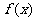 在
在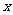 =64处取得最小值,此时,
=64处取得最小值,此时,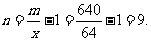
故需新建9个桥墩才能使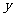 最小。
最小。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com