
(18) 本题主要考查正弦、余弦定理, 三角公式变换, 三角形面积公式及向量运算等基础知识,同时考查运算求解能力。满分14分。
(Ⅰ) 解: 利用正弦定理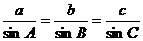 , 得
, 得
sinCcosB+sinBcosC = 4sinAcosA,
sin(B+C) = 4sinAcosA,
即 sinA = 4cosAsinA,
所以cosA =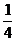 .
……………………(7分)
.
……………………(7分)
(Ⅱ) 解: 由(I), 得
sinA =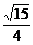 ,
,
由题意,得
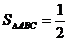 bcsinA=
bcsinA=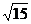 ,
,
所以bc = 8,
因此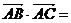 2 .
…………………(14分)
2 .
…………………(14分)
(19) 本题主要考查排列组合, 随机事件的概率和随机变量的分布列、数学期望等概念, 同时考查抽象概括能力。满分14分。
(Ⅰ) 解: 记“取出的数各位数字互不相同”为事件B, 则
P(B)=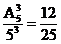 .
…………………(5分)
.
…………………(5分)
(Ⅱ) 解: 随机变量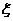 的取值为0, 1, 2.
的取值为0, 1, 2. 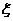 的分布列是
的分布列是
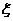 |
0 |
1 |
2 |
|
P |
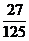 |
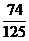 |
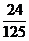 |
…………………(11分)
所以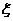 的数学期望
的数学期望
E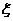 =0×
=0×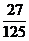 +1×
+1×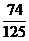 +2×
+2×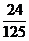 =
=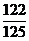 . …………………(14分)
. …………………(14分)
(20) 本题主要考查空间线线、线面、面面位置关系, 空间向量的概念与运算等基础知识,同时考查空间想象能力和推理运算能力。满分15分。
方法一:
(Ⅰ) 解: 如图, 在平面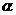 内, 过点P作PM⊥EF, 点M为垂足, 连结BM, 则∠BMP为二面角
内, 过点P作PM⊥EF, 点M为垂足, 连结BM, 则∠BMP为二面角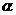 -EF-
-EF-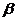 的平面角. 以点P为坐标原点, 以直线PM为x轴, 射线PB为z轴的正半轴, 建立如图所示的空间直角坐标系Pxyz.
的平面角. 以点P为坐标原点, 以直线PM为x轴, 射线PB为z轴的正半轴, 建立如图所示的空间直角坐标系Pxyz.
 在Rt△BMC中,
在Rt△BMC中,
由∠BCM=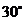 , CB
, CB  = 4, 得
= 4, 得
CM = , BM
=2.
, BM
=2.
在Rt△BMP中,
由∠BMP=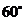 , BM =2, 得
, BM =2, 得
MP = 1, BP =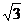 .
.
故P(0,0,0), B(0, 0,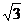 ), C(-1,-
), C(-1,- , 0), M(-1,0,0).
, 0), M(-1,0,0).
由∠ACM=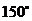 , 得
, 得
A(1,-4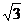 , 0).
, 0).
所以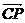 = (1,
= (1, ,0),
,0), 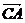 = (2,-
= (2,- ,0),
,0),
则 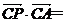 -10,
-10,
cos∠ACP = -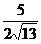 ,
,
sin∠ACP = 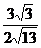 .
.
因此S△ACP=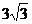 .
…………………(7分)
.
…………………(7分)
(Ⅱ) 解: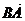 =(1,-4
=(1,-4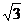 ,-
,-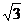 ),
),  =(0,-2
=(0,-2
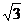 ,0),
,0),
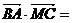 24,
24,
cos<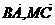 >=
>=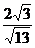 ,
,
所以AB与EF所成角的正切值为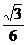 .
.  …………………(15分)
…………………(15分)
 因此AB与EF所成角的正切值为
因此AB与EF所成角的正切值为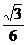 .
…………………(15分)
.
…………………(15分)
(21) 本题主要考查抛物线的几何性质,直线与抛物线的位置关系等基础知识,考查解析
几何的基本思想方法和综合解题能力。满分15分。
(Ⅰ) 解: 设抛物线C的方程是x2 = ay,
则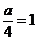 ,
,
即a = 4.
故所求抛物线C的 方程为x2 = 4y .
…………………(5分)
方程为x2 = 4y .
…………………(5分)
(Ⅱ) 解: 设P(x1, y1), Q(x2, y2),
则抛物线C在点P处的切线方程是
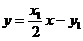 ,
,
直线PQ的方程是
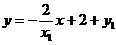 .
.
将上式代入抛物线C的方程, 得
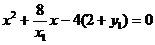 ,
,
故 x1+x2 =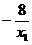 ,
x1x2 =-8-4y1 ,
,
x1x2 =-8-4y1 ,
所以 x2=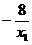 -x1 , y2=
-x1 , y2=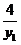 +y1+4
.
+y1+4
.
而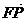 =(x1,
y1-1),
=(x1,
y1-1),
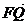 =(x2 , y2-1)
,
=(x2 , y2-1)
,
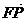 ×
×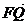 =x1
x2+(y1-1)
(y2-1)
=x1
x2+(y1-1)
(y2-1)
=x1 x2+y1 y2-(y1+y2)+1
=-4(2+y1)+ y1(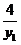 +y1+4)-(
+y1+4)-(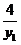 +2y1+4)+1
+2y1+4)+1
=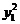 -2y1 -
-2y1 -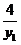 -7
-7
=(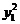 +2y1+1)-4(
+2y1+1)-4(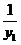 +y1+2)
+y1+2)
=(y1+1)2-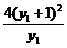
=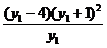
=0,
故 y1=4, 此时, 点P的坐标是(±4,4) .
经检验, 符合题意.
所以, 满足条件的点P存在, 其坐标为P(±4,4). …………………(15分)
(22) 本题主要考查函数的基本性质、导数的概念、导数的应用等基础知识,同时考查逻辑推理能力和创新意识。满分14分。
(Ⅰ) 解: 当a = 0时, f (x)=x3-4x2+5x ,
 >0,
>0,
所以 f (x)的单调递增区间为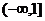 ,
, 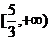 .
…………………(6分)
.
…………………(6分)
(Ⅱ) 解: 一方面由题意, 得
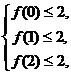
即
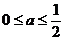 ;
;
另一方面当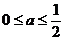 时,
时,
f (x) = (-2x3+9x2-12x+4)a+x3-4x2+5x ,
令g(a) = (-2x3+9x2-12x+4)a+x3-4x2+5x, 则
g (a) ≤ max{ g(0), g(
(a) ≤ max{ g(0), g(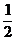 ) }
) }
= max{x3-4x2+5x , 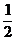 (-2x3+9x2-12x+4)+x3-4x2+5x }
(-2x3+9x2-12x+4)+x3-4x2+5x }
= max{x3-4x2+5x , 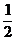 x2-x+2 },
x2-x+2 },
f (x) = g(a)
≤ max{x3-4x2+5x , 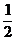 x2-x+2 },
x2-x+2 },
又 {x3-4x2+5x}=2,
{x3-4x2+5x}=2, 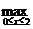 {
{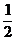 x2-x+2}=2, 且f (2)=2,
x2-x+2}=2, 且f (2)=2,
所以当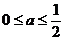 时, f (x)在区间[0,2]上的最大值是2.
时, f (x)在区间[0,2]上的最大值是2.
综上, 所求
a的取值范围是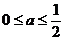 .
…………………(14分)
.
…………………(14分)
(11) 1 (12)
1 (13)
(-1)n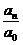 ( (-1)n与
( (-1)n与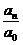 每对一个得2分)
每对一个得2分)
(14) 1 (15) 169
(16) 15 (17)
[1,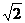 )
)
( 1) B (2)
D (3) C (4) A (5) D
1) B (2)
D (3) C (4) A (5) D
(6) D (7) C (8) C (9) A (10) B
(18) (本题满分14分) 在△ABC中, 角A, B, C所对的边分别为a, b, c, 且满足
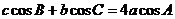 .
.
(Ⅰ) 求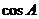 的值;
的值;
(Ⅱ) 若△ABC的面积是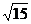 , 求
, 求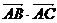 的值.
的值.
(19) (本题满分14分) 在由1,2,3,4,5组成可重复数字的三位数中任取一个数.
(Ⅰ) 求取出的数各位数字互不相同的概率;
(Ⅱ) 记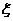 为组成这个数的各位数字中不同的偶数个数(例如:若这个数为212, 则
为组成这个数的各位数字中不同的偶数个数(例如:若这个数为212, 则
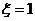 ). 求随机变量
). 求随机变量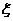 的分布列及其数学期望E
的分布列及其数学期望E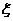 .
.
(20) (本题满分15分) 如图, 在平面内直线EF与线段AB相交于C点, ∠BCF=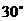 , 且
, 且
AC = CB = 4, 将此平面沿直线EF折成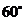 的二面角
的二面角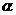 -EF-
-EF-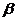 , BP⊥平面
, BP⊥平面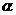 , 点P
, 点P
为垂足.
(Ⅰ) 求△ACP的面积;
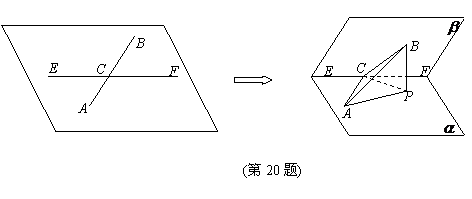 (Ⅱ) 求异面直线AB与EF所成角的正切值.
(Ⅱ) 求异面直线AB与EF所成角的正切值.
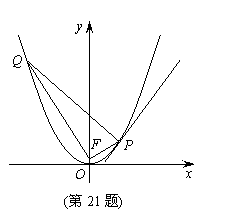 (21) (本题满分15分) 已知抛物线C的顶点在原点, 焦点为F(0, 1).
(21) (本题满分15分) 已知抛物线C的顶点在原点, 焦点为F(0, 1).
(Ⅰ) 求抛物线C的方程;
(Ⅱ) 在抛物线C上是否存在点P, 使得过点P的直
线交C于另一点Q, 满足PF⊥QF, 且PQ与C
在点P处的切线垂直? 若存在, 求出点P的坐标;
若不存在, 请说明理由.
(22) (本题满分14分)已知函数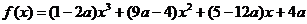 (
(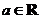 ).
).
(Ⅰ) 当a = 0时, 求函数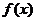 的单调递增区间;
的单调递增区间;
(Ⅱ) 若函数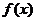 在区间[0, 2]上的最大值为2, 求a的取值范围.
在区间[0, 2]上的最大值为2, 求a的取值范围.
数学测试卷(理科)答案及评分参考
说明:
(11) 若实数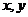 满足不等式组
满足不等式组 则3x-y的最小值是________.
则3x-y的最小值是________.
(12) 若等比数列{an}的前n项和Sn满足: an+1=a1 Sn+1(n∈N*), 则a1=________.
(13) 已知a0≠0.
①
设方程a0x+a1=0的1个根是x1, 则x1=-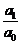 ;
;
②
设方程a0x2+a1x+a2=0的2个根是x1, x2,
则x1 x2=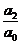 ;
;
③
设方程a0x3+a1x2+a2x+a3=0的3个根是x1, x2,
x3, 则x1 x2
x3=-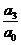 ;
;
④
设方程a0x4+a1x3+a2x2+a3x+a4=0的4个根是x1, x2,
x3, x4, 则x1 x2 x3 x4=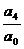 ;
;
……
由以上结论, 推测出一般的结论:
设方程a0xn+a1xn-1+a2xn-2+…+an-1x+an=0的n个根是x1, x2,
…, xn
,
则x1 x2…xn=________.
(14) 设直线3x+4y-5=0与圆C1:  交于A, B两点, 若圆C2的圆心在
交于A, B两点, 若圆C2的圆心在 线段AB上, 且圆C2与圆C1相切, 切点在圆C1的劣弧
线段AB上, 且圆C2与圆C1相切, 切点在圆C1的劣弧 上, 则圆C2的半径的最大值是________.
上, 则圆C2的半径的最大值是________.
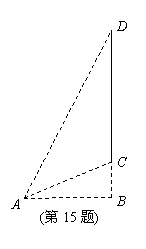 (15)
如图, 某城市的电视发射塔CD建在市郊的小山上, 小山的高
(15)
如图, 某城市的电视发射塔CD建在市郊的小山上, 小山的高
BC为35米, 在地面上有一点A, 测得A, C间的距离为91米,
从A观测电视发射塔CD的视角(∠CAD)为 , 则这座电视
, 则这座电视
发射塔的高度CD为________米.
(16) 将5人分成3组, 每组至多2人, 则不同的分组方式种数是________.
(17) 若函数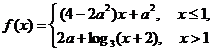 在区间
在区间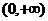 上单调递增, 则实数a的取值范围是________.
上单调递增, 则实数a的取值范围是________.
(1) 设非空集合A, B满足A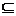 B, 则
B, 则
(A) 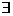 x0∈A, 使得x0
x0∈A, 使得x0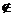 B (B)
B (B)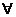 x∈A, 有x∈B
x∈A, 有x∈B
(C) 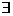 x0∈B, 使得x0
x0∈B, 使得x0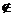 A (D)
A (D)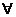 x∈B, 有x∈A
x∈B, 有x∈A
(2) 在二项式(x-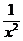 )6的展开式中,
常数项是
)6的展开式中,
常数项是
(A) -10 (B) -15 (C) 10 (D) 15
(3) 已知a, b是实数, 则“a = b”是“a3 = b3 ”的
b是实数, 则“a = b”是“a3 = b3 ”的
(A) 充分而不必要条件 (B) 必要而不充分条件
(C) 充分必要条件 (D) 既不充分也不必要条件
(4) 若复数z与其共轭复数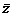 满足: |z|=
满足: |z|=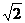 , z
+
, z
+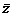 =2, 则
=2, 则
(A) z2- 2z+2=0 (B) z2-2z-2=0
2z+2=0 (B) z2-2z-2=0
(C) 2z2-2z+1=0 (D) 2z2-2z-1=0
 (5) 某程序框图如图所示, 该程序运行后输出的k的值是
(5) 某程序框图如图所示, 该程序运行后输出的k的值是
(A) 4 (B) 5
(C) 6 (D) 7
(6) 设向量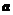 ,
, 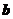 满足:
满足: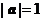 ,
, 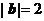 ,
, 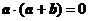 ,
,
则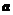 与
与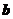 的夹角是
的夹角是
(A) 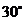 (B)
(B) 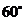
(C)  (D)
(D) 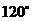
(7) 在Rt△ABC中, ∠A= , ∠B=
, ∠B=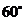 , AB=1. 若圆O的圆心在直角边AC上, 且与AB
, AB=1. 若圆O的圆心在直角边AC上, 且与AB
和BC所在的直线都相切, 则圆O的半径是
 (A)
(A) 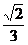 (B)
(B) 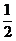
(C) 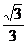 (D)
(D) 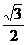
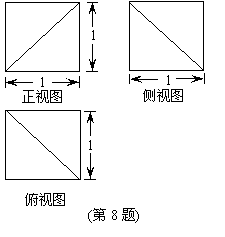
(8)
若某多面体的三视图(单位: cm)如图所示, 则
则
此多面体的体积是
(A) 
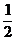 cm3
(B)
cm3
(B)  cm3
cm3
(C) 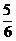 cm3 (D)
cm3 (D)
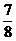 cm3
cm3
(9)
过双曲线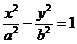 (a>0, b>0)的右焦点F作圆
(a>0, b>0)的右焦点F作圆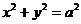 的切线FM(切点为M),
的切线FM(切点为M),
交y轴于点P. 若M为线段FP的中点, 则双曲线的离心率是
(A) 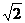 (B)
(B)
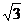 (C)
2 (D)
(C)
2 (D)
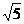
(10) 在直角坐标系中, 如果两点A(a, b), B(-a, -b)在函数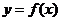 的图象上, 那么称
的图象上, 那么称
[A, B]为函数f (x)的一组关于原点的中心对称点 ([A , B]与[B, A]看作一组). 函数
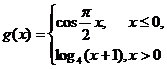 关于原点的中心对称点的组数为
关于原点的中心对称点的组数为
(A) 1 (B) 2 (C) 3 (D) 4
非选择题部分 (共100分)
35. 2009年11月18日,中越陆地边界勘界文件签字仪式在北京举行。中越陆地边界经过双方历时10年的共同努力已全线勘定。签署的文件包括《中越陆地边界勘界议定书》及其附图、《中越陆地边界管理制度协定》和《中越陆地边境口岸及其管理制度协定》。这一外交成果
①标志着中越两国关系开始正常化 ②有利于共同致力于两国边境地区的长治久安
③有利于两国共同努力维护南海的和平稳定 ④体现了坚持和平共处五项原则处理国际关系
A.①②③ B.①②④ C.①③④ D.②③④
34. 2009年11月23日,新疆维吾尔自治区十一届人大常委会十五次会议对《自治区民族团结教育条例(草案)》进行了初次审议,旨在通过地方性立法将新疆民族团结教育工作纳入法制化、规范化和日常化管理轨道。 这表明
①要依法推进维护民族团结教育工作 ②地方人大常委会享有国家立法权
③立法机关要确保民族团结教育有法必依 ④这有利于维护新疆各族人民的最高利益
A.①② B.①④ C.②③ D.③④
33. 党是整个社会的表率,党的各级领导干部又是全党的表率。各级党组织和领导干部的作风如何,对全党全社会有着很强的示范性和导向作用。这是因为
A.中国共产党是中国人民的先锋队 B.党的各级领导干部行使国家权力
C.中国共产党代表全体公民的利益 D.中国共产党对民主党派全面领导
32.近日,北京市人大少数民族代表小组正式成立。该小组由23名少数民族市人大代表组成,成立后将致力于民族工作相关的专题调研,参与民族工作相关的议案督办,组织民族工作相关的立法和执法检查,参加民族文化经济交流活动。这表明
A.北京市人大依法加强执法监督 B.少数民族地区实行民族区域自治
C.各级人大要有适当名额的少数民族代表 D.人大加大依法行政、公正司法力度
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com