1．A　 2．B　 3．A　 4．A　 5．D　 6．D　 7．B　 8．B　　 9．C　 10．C

填空题(18分)

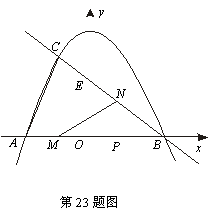
23．(本题10分)已知：如图，抛物线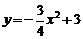与x轴交于点A，点B，与直线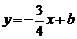相交于点B，点C，直线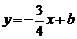与y轴交于点E．

(1)写出直线BC的解析式；

(2)求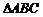的面积；

(3)若点M在线段AB上以每秒1个单位长度的速度从A向B运动(不与A，B重合)，同时，点N在射线BC上以每秒2个单位长度的速度从B向C运动．设运动时间为t秒，请写出的面积S与t的函数关系式，并求出点M运动多少时间时，的面积最大，最大面积是多少？

2010年深圳市初中毕业生学业考试 数学模拟试卷(十)

选择题(30分)

22．(本题9分)已知：Rt△ABC的斜边长为5，斜边上的高为2，将这个直角三角形

　　 放置在平面直 角坐标系中，使其斜边AB与x轴重合(其中OA<OB)，直角顶点

　　 C落在y轴正半轴上(如图1)．

(1)求线段OA、OB的长和经过点A、B、C的抛物线的关系式；

(2)如图2，点D的坐标为(2，0)，点P(m，n)是该抛物线上的一个动点(其中m>0，n>0)，连接DP交BC于点E．连接CD、CP(如图3)，△CDP是否有最大面积？若有，求出△CDP的最大面积和此时点P的坐标；若没有，请说明理由．

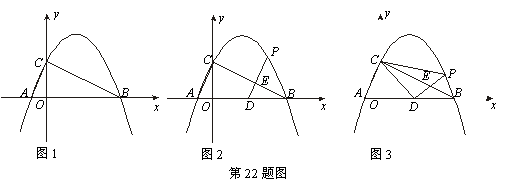
21．(本题8分)已知△ABC中，∠BAC=36°，AB=AC=2，动点D在CB的延长线上

运动，动点E 在BC的延长线上运动，且保持∠DAE的值为108°．

设，．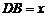

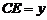(1)求y与x之间的函数关系式；

(2)已知直线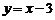与(1)中函数图象的交点坐标是(a，b)，求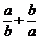的值；

(3)求BC的长．

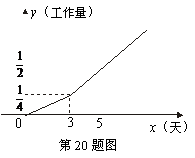
20．(本题8分)某家庭装修房屋，由甲、乙两个装修公司合作完成，选由甲装修公司

单独装修3天，剩下的工作由甲、乙两个装修公司合作完成．工程进度满足如图

所示的函数关系，该家庭共支付工资8000元．

(1)完成此房屋装修共需多少天？

(2)若按完成工作量的多少支付工资，甲装修公司应得多少元？

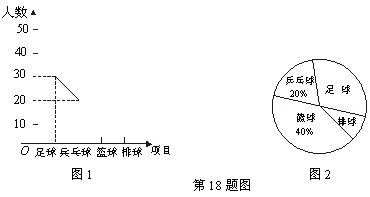
19．(本题6分)某中学学生会为了解该校学生喜欢球类活动的情况，采取抽样调查的

方法，从足球、乒乓球、篮球、排球等四个方面调查了若干名学生的兴趣爱好，

并将调查的结果绘制成如下的两幅不完整的统计图(如图1，图2要求每位同学只

能选择一种自己喜欢的球类；图中用乒乓球、足球、排球、篮球代表喜欢这四种

球类中的某一种球类的学生人数)，请你根据图中提供的信息解答下列问题：

(1)在这次研究中，一共调查了多少名学生？

(2)喜欢排球的人数在扇形统计图中所占的圆心角是多少度？

(3)补全频数分布折线统计图．

18．(本题6分)先化简，再求值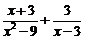：，其中．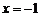

17．(本题5分)计算：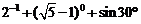

16．如图，一名男生推铅球，铅球行进高度y(单位：m)与水平距

离x(单位：m)之间的关系是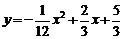．则他

将铅球推出的距离是______________m．

15．有一个运算程序，可以使：a⊕b =n(n为常数)时，得(a+1)⊕b = n+1，a⊕(b+1)

= n-2现在已知1⊕1=2，那么2008⊕2008=____________．