
4.对性腺组织细胞进行荧光标记,等位基因A、a都被标记为黄色,等位基因B、b都被标记为绿色,在荧光显微镜下观察处于四分体时期的细胞。下列有关推测合理的是( )
A.若这2对基因在1对同源染色体上,则有1个四分体中出现2个黄色、2个绿色荧
光点
B.若这2对基因在1对同源染色体上,则有1个四分体中出现4个黄色、4个绿色荧光点
C.若这2对基因在2对同源染色体上,则有1个四分体中出现2个黄色、2个绿色荧光点
D.若这2对基因在2对同源染色体上,则有1个四分体中出现4个黄色、4个绿色荧
光点
3.已知某闭花授粉植物高茎对矮茎为显性,红花对白花为显性,两对性独立遗传。现用纯合的高茎红花与矮茎白花杂交,F1自交,播种所有的F2,假定所有的F2植株都能成活,F1植株开花时,拔掉所有的白花植株,假定剩余的每株F2植株自交收获的种子数量相等,且R的表现型符合遗传的基本定律,从理论上讲,F3中表现白花植株的比例为( )
A.1/4 B.1/6 C.1/8 D.1/16
2.下列有关生物膜系统的叙述不正确的一项是 ( )
A.生物膜系统是真核生物所特有的
B.生物膜系统使各个细胞器组成生命活动的统一体
C.细胞内分割的膜性区室的出现使细胞器间完全独立
D.细胞内分割的膜性区室的出现减少了细胞内各种生化反应的相互干扰
1.下列有关动物细胞编程性死亡的说法正确的是 ( )
A.细胞癌变属于细胞编程性死亡
B.细胞编程性死亡属于细胞的正常生理过程
C.细胞编程性死亡属于细胞的正常分化
D.细胞编程性死亡与基因表达无关
21.[解答](Ⅰ)令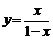 ,解得
,解得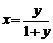 ,由
,由 ,解得
,解得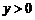 ,
,
∴函数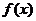 的反函数
的反函数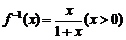 ,则
,则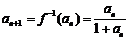 ,得
,得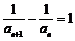 .
.
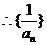 是以2为首项,l为公差的等差数列,故
是以2为首项,l为公差的等差数列,故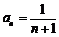 .
.
(Ⅱ)∵ ,∴
,∴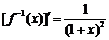 ,
,
∴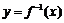 在点
在点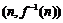 处的切线方程为
处的切线方程为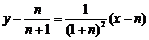 ,
,
令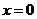 ,
得
,
得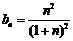 ,∴
,∴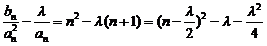 ,
,
∵仅当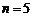 时取得最小值,∴
时取得最小值,∴ ,解之
,解之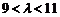 ,
,
∴ 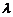 的取值范围为
的取值范围为 .
.
(Ⅲ)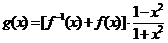
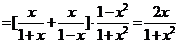 ,
,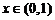 .
.
则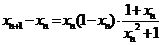 ,
,
因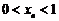 ,则
,则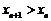 ,显然
,显然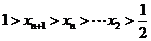 .
.
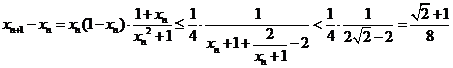 ·
·
∴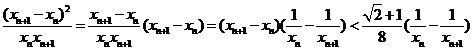
∴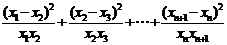
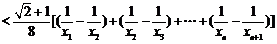
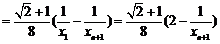
∵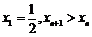 ,∴
,∴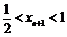 ,
,
∴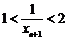 ,∴
,∴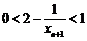
∴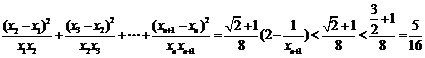 .
.
21.(本小题满分14分)
已知函数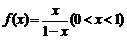 的反函数为
的反函数为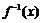 ,数列
,数列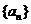 和
和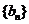 满足:
满足: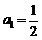 ,
,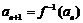 ,函数
,函数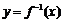 的图象在点
的图象在点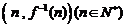 处的切线在
处的切线在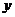 轴上的截距为
轴上的截距为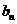 .
.
(Ⅰ)求数列{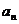 }的通项公式;
}的通项公式;
(Ⅱ)若数列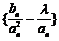 的项仅
的项仅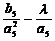 最小,求
最小,求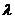 的取值范围;
的取值范围;
(Ⅲ)令函数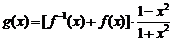 ,
,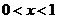 ,数列
,数列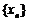 满足:
满足: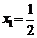 ,
,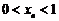 ,且
,且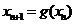 ,其中
,其中 .证明:
.证明: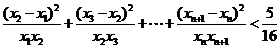 .
.
20.[解答](Ⅰ)分别以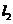 、
、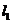 为
为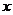 轴,
轴,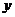 轴建立如图坐标系.据题意得
轴建立如图坐标系.据题意得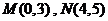 ,
,

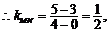

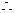 线段
线段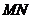 的垂直平分线方程为:
的垂直平分线方程为: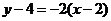 ),
),
故圆心A的坐标为(4,0),
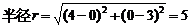 ,
,
∴弧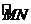 的方程:
的方程: (0≤x≤4,y≥3)
(0≤x≤4,y≥3)
(Ⅱ)设校址选在B(a,0)(a>4),

整理得: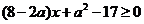 ,对0≤x≤4恒成立(﹡)
,对0≤x≤4恒成立(﹡)
令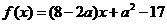
∵a>4
∴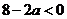 ∴
∴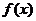 在[0,4]上为减函数
在[0,4]上为减函数
∴要使(﹡)恒成立,当且仅当
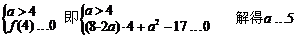 ,
,
即校址选在距 最近5km的地方.
最近5km的地方.
20.(本小题满分13分)
如图,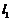 、
、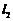 是通过某城市开发区中心
是通过某城市开发区中心 的两条南北和东西走向的街道,连接
的两条南北和东西走向的街道,连接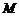 、
、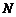 两地之间的铁路线是圆心在
两地之间的铁路线是圆心在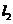 上的一段圆弧.若点
上的一段圆弧.若点 在点
在点 正北方向,且
正北方向,且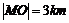 ,点
,点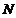 到
到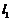 、
、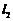 的距离分别为
的距离分别为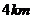 和
和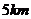 .
.
(Ⅰ)建立适当坐标系,求铁路线所在圆弧的方程;
(Ⅱ)若该城市的某中学拟在点 正东方向选址建分校,考虑环境问题,要求校址到点
正东方向选址建分校,考虑环境问题,要求校址到点 的距离大于
的距离大于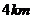 ,并且铁路线上任意一点到校址的距离不能少于
,并且铁路线上任意一点到校址的距离不能少于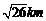 ,求该校址距点O的最近距离(注:校址视为一个点).
,求该校址距点O的最近距离(注:校址视为一个点).
19. [解答] (Ⅰ)设点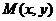 ,由
,由 得
得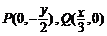 ,
,
由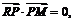 得
得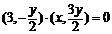 即
即 .
.
(Ⅱ)由题意可知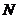 为抛物线
为抛物线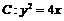 的焦点,且
的焦点,且 为过焦点
为过焦点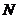 的直线与抛物线
的直线与抛物线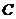 的两个交点.
的两个交点.
当直线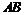 斜率不存在时,得A(1,2),B(1,-2),|AB|
斜率不存在时,得A(1,2),B(1,-2),|AB|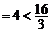 ,不合题意;
,不合题意;
当直线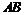 斜率存在且不为0时,设
斜率存在且不为0时,设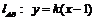 ,代入
,代入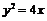 得
得
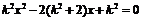
则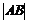
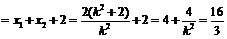 ,解得
,解得 ,
,
代入原方程得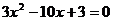 ,得
,得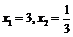 或
或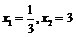 ,
,
由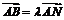 ,得
,得
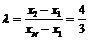 或4.
或4.
19.(本小题满分12分)
已知点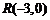 ,点
,点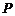 在
在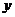 轴上,点
轴上,点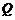 在
在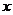 轴的正半轴上,点
轴的正半轴上,点 在直线
在直线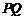 上 ,且满足
上 ,且满足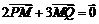 ,
,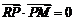 .
.
(Ⅰ)当点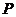 在
在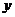 轴上移动时,求点
轴上移动时,求点 的轨迹
的轨迹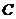 的方程;
的方程;
(Ⅱ)设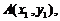
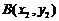 为轨迹
为轨迹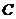 上两点,且
上两点,且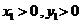 ,
,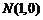 ,求实数
,求实数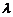 ,使
,使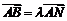 ,且
,且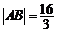 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com