
3. --- Did you enjoy yourself at the party?
---Sorry to say I didn’t. It was _____ a meeting than a party.
A. more of B. rather like C. less of D. more or less
2. Many people are still in _____ habit of writing silly words in _____ public places.
A. the; the B. / ; / C. the; / D. / ; the
1. --- Is there anything wrong with my baby?
--- Nothing _____._____.
A. seriously; Take easy B. seriously; Take it easy
C. serious; Take easy D. serious; Take it easy
3.性质通过解析式给出的
这类问题有解析式,但考虑的方向不是代人求值问题,而是通过观察解析的特点,从而得到函数的性质,用性质去解决相关问题,考虑的性质一般是先看看函数的对称性,再看看单调性,进一步作出相关的草图就可以解决了。
[例5] (2009·江苏文理10) 已知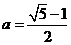 ,函数
,函数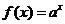 ,若实数
,若实数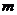 、
、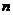 满足
满足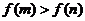 ,则
,则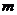 、
、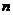 的大小关系为 .
的大小关系为 .
答案:m<n
分析:本题给出的是指数函数解析式,并且知道底数的范围,其实质是告诉函数的单调性进一步用函数的单调性去解决比较大小的问题。
解:考查指数函数的单调性。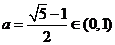 ,函数
,函数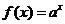 在R上递减。由
在R上递减。由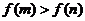 得:m<n
得:m<n
[例6]已知函数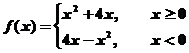 若
若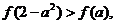 则实数
则实数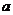 的取值范围是
的取值范围是
A 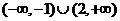 B
B 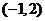 C
C 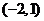 D
D 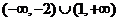
分析:本题载体是分段函数,解析式的主要作用是告诉函数的单调性,只要知道函数的单调性问题就简单了。
解:由题知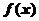 在
在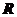 上是增函数,由题得
上是增函数,由题得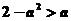 ,解得
,解得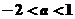 ,故选择C。
,故选择C。
解决策略:从上面两题来看,条件告诉了解析式貌似是代人求值问题,其实质是考查函数性质的问题,只要能从解析式中判断出函数的性质,问题就能得到顺利的解决。
高考的考查是能力的考查,能不能在高考中取得优异的成绩仅仅靠大量的训练是不够的,这需要透过问题看到实质,需要从历届考题中去发现考题的规律和问题本质,这样才能达到事半功倍的效果。而函数问题的本质是变量间的关系研究,而这种研究恰好是建立在性质基础之上的,而性质的给出和去向是解题的关键,以上就是对函数性质问题处理做一下简单的探讨。
参考文献:《高中数学课程标准解读》 人民教育出版社
《抽象函数性质寻根》 万尔遐 中学数学月刊
《十年高考》
2.性质通过方程和不等式给出的
在7大数学思想中,人们把“函数方程思想”放在首位,函数与方程本来就是一对孪生兄弟. 函数的解析式 y = f (x)可视二元方程F (x,y) = 0;反之,对二元方程F (x,y),也可把y视作x的函数.
因此,函数不仅可用解析式定义,还可用方程或不等式定义.
这类问题通常是考查的抽象函数有关问题,抽象函数因其没有解析式,其性质以方程(或不等式)给出而成为解题依据. 所以在解题时要搞清楚常见方程和不等式所告诉的含义是什么,常见的方程表述有
①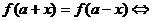
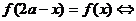
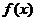 的图象关于直线
的图象关于直线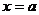 对称.
对称.
② 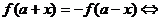
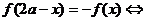
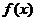 的图象关于点
的图象关于点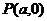 对称.
对称.
③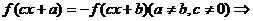
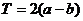 是函数
是函数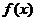 的一个周期
的一个周期
④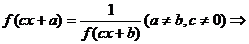
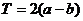 是函数
是函数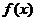 的一个周期
的一个周期
⑤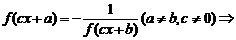
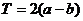 是函数
是函数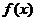 的一个周期
的一个周期
⑥指数函数满足f ( x+y) = f (x)·f ( y)对数函数满足f (x·y) = f (x) f ( y),f ( xy) = y f (x);
⑦正弦函数满足f (x±y) = f (x) g ( y) ±f (y) g (x);
⑧余弦函数满足f ( x±y)= f ( x) f
( y)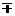 g( x) g( y);
g( x) g( y);
⑨正切函数满足f (x±y) =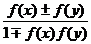 .
.
[例3]定义在R上的函数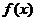 的图象关于点
的图象关于点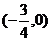 对称,且满足
对称,且满足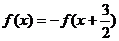 ,
,
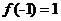 .
.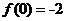 ,则
,则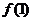 +
+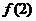 +
+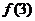 +--------+
+--------+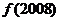 =_____________.
=_____________.
分析:由方程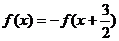 知周期,又因为关于
知周期,又因为关于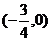 对称,通过联系三角函数知此函数还是偶函数,这样问题就简单了。
对称,通过联系三角函数知此函数还是偶函数,这样问题就简单了。
解: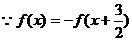 ,
,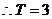 是
是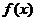 的一个周期,又
的一个周期,又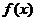 的图象关于点
的图象关于点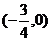 对称,
对称,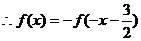 ,
,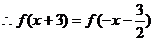 ,故
,故 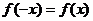 ,
,
即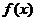 是偶函数,
是偶函数,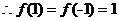 ,
,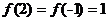 ,
,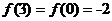 ,
,
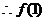 +
+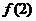 +
+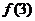 =0,故
=0,故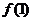 +
+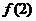 +
+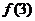 +--------+
+--------+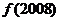 =
=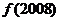 =1.
=1.
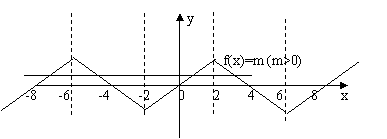
[例4]( 2009·山东文理16)已知定义在R上的奇函数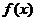 ,满足
,满足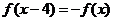 ,且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间
,且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间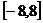 上有四个不同的根
上有四个不同的根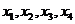 ,则
,则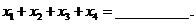


分析:本题综合考查了函数的奇偶性,单调性,对称性,周期性,以及由函数图象解答方程问题,
运用数形结合的思想和函数与方程的思想解答问题.
 解:因为定义在R上的奇函数,满足
解:因为定义在R上的奇函数,满足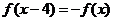 ,所以
,所以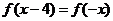 ,所以, 由
,所以, 由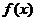 为奇函数,所以函数图象关于直线
为奇函数,所以函数图象关于直线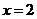 对称且
对称且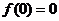 ,由
,由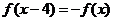 知
知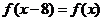 ,所以函数是以8为周期的周期函数,又因为
,所以函数是以8为周期的周期函数,又因为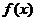 在区间[0,2]上是增函数,所以
在区间[0,2]上是增函数,所以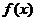 在区间[-2,0]上也是增函数.如图所示,那么方程f(x)=m(m>0)在区间
在区间[-2,0]上也是增函数.如图所示,那么方程f(x)=m(m>0)在区间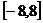 上有四个不同的根
上有四个不同的根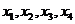 ,不妨设
,不妨设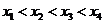 由对称性知
由对称性知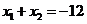
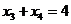 所以
所以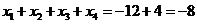
答案:-8
解决策略:函数的解析式与函数的方程式在
解题上比优劣,前者最大的优势是求自
变量对应的函数值,而在研究函数的性
质方面,有时还不如方程式简便.所以有关抽象函数的
“方程题型”,往往是函数的“性质题型”.所以在解决一个问题时当看到方程就考虑函数的奇偶性或周期性,当出现不等式就考虑单调性。
1. 性质通过数学语言给出的
这类问题一般没有解析式,也没有函数方程,有的是常见的函数性质语言比如:单调递增,奇函数等等,它通常和不等式联立在一起考查,处理方式主要是通过它所给的性质画出函数的草图然后解决就可以了。
[例1](2009·辽宁文理9)已知偶函数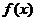 在区间
在区间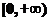 上单调增加,则
上单调增加,则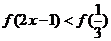 的x取值范围是
的x取值范围是
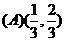
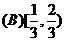
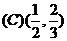
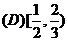
答案: A
分析:此题是典型的由数学语言给出的问题,没有解析式,只需要弄清楚偶函数的作用以及函数单调性在解不等式中处理就可以了。
解:由已知有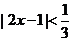 ,即
,即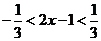 ,∴
,∴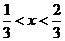 。
。
[例2](2005年全国)设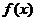 是定义在R上的奇函数,且y=
是定义在R上的奇函数,且y=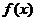 的图像关于直线
的图像关于直线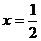 对称,则
对称,则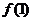 +
+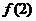 +
+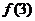 +
+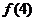 +
+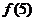 =_____________.
=_____________.
分析:这是一道典型的“奇偶性”+“关于直线x=k”对称,只要类比一下正弦函数就不难得出函数的周期为2.
解析: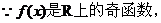
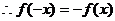 ,
,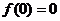 .又y=
.又y=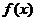 的图像关于直线
的图像关于直线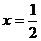 对称,
对称,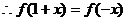 ,且
,且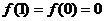 ,
,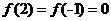 .
.
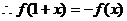 ,
,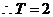 是
是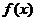 的一个周期. 故
的一个周期. 故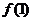 +
+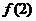 +
+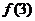 +
+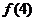 +
+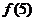 =0
=0
解决策略:这类通过语言叙述的,只要根据语言特征作出相应图像,或者转化成相应的方程或不等式就可以得到顺利解决。一般奇偶性和周期性问题可以转化成方程,而函数的单调性则转化成不等式问题处理。
4. “奇偶性”+“关于直线x=k”对称,求出函数周期。
高考的考查题型:
3. 周期性 周期性主要研究函数值有规律的出现,在解决三角函数里面体现的更明显
2. 奇偶性(对称性)奇偶性主要研究函数的整体性质,奇偶性研究主要两种形式:一个是图形一个是方程的形式。
1. 单调性 单调性是函数性质的核心,它研究函数的局部的变化趋势,在函数值的比较大小,求函数的值域,解相关的不等式方面有着重要的应用。在高中阶段函数单调性研究分为两个阶段,第一阶段:通过定义研究的,第二阶段:通过导数研究的。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com